Контрольные вопросы для самоконтроля по усвоению теоретического материала, здесь же предлагается комплекс упражнений для самостоятельной работы
 Скачать 7.87 Mb. Скачать 7.87 Mb.
|
|
По теме данной главы студент должен уметь:
IV. АКСИОМАТИЧЕСКОЕ ПОСТРОЕНИЕ СИСТЕМЫ НАТУРАЛЬНЫХ ЧИСЕЛ Литература [1] гл. III §§ 13, 14,15 При аксиоматическом построении какой-либо теории соблюдаются определенные правила:
При аксиоматическом построении теории по существу все утверждения выводятся путем доказательства из аксиом. Поэтому к системе аксиом предъявляются особые требования. Прежде всего, она должна быть непротиворечивой и независимой. Система аксиом называется непротиворечивой, если из нее нельзя логически вывести два взаимно исключающих друг друга предложения. Непротиворечивая система аксиом называется независимой, если никакая из аксиом этой системы не является следствием других аксиом этой системы. Аксиомы, как правило, являются отражением многовековой практической деятельности людей, и этим обусловливается их справедливость. В качестве основного понятия при аксиоматическом построении арифметики натуральных чисел взято отношение «непосредственно следовать за», заданное на непустом множестве N. Известными также считаются понятия множества, элемента множества и другие теоретико-множественные понятия, а также правила логики. Элемент, непосредственно следующий за элементом а, обозначают а'. Суть отношения «непосредственно следовать за» раскрывается в следующих аксиомах, предложенных итальянским математиком Дж. Пеано в 1891 году. Аксиома 1. В множестве N существует элемент, непосредственно не следующий ни за каким элементом этого множества. Его называют единицей и обозначают символом 1. Аксиома 2. Для каждого элемента а из N существует единственный элемент а', непосредственно следующий за а. Аксиома 3. Для каждого элемента а из N существует не более одного элемента, за которым непосредственно следует а. Аксиома 4. (Аксиома индукции). Всякое подмножество М множества N совпадает с N, если обладает свойствами: 1) 1 содержится в М; 2) из того, что любой элемент а содержится в М, следует, что и а' содержится в М. Сформулированные аксиомы часто называют аксиомами Пеано, а аксиому четвертую – аксиомой индукции. Запишем эти аксиомы в символической форме. А1)(1N)(aN) а'1; А2)(aN)(!bN) а'=b А3) (а,b,с N )с = а' с = b' а = b; A4) MN1M(aMа'M) M=N Используя отношение «непосредственно следовать за» и аксиомы Пеано 1-4, можно дать следующее определение натурального числа. ___________________________________________________________________ Определение 1. Множество N. для элементов которого установлено отношение «непосредственно следовать за», удовлетворяющее аксиомам 1-4, называется множеством натуральных чисел, а его элементы натуральными числами. ______________________________________________________________________________________________ ___________________________________________________________________ Определение 2. Если натуральное число b непосредственно следует за числом а, то число а называется непосредственно предшествующим (предшествующим) числу b. ______________________________________________________________________________________________ Теорема 1. Единица не имеет предшествующего натурального числа (истинность теоремы вытекает сразу из аксиомы А1). Теорема 2. Каждое натуральное число а, отличное от единицы имеет предшествующее число b, такое, что b' = а. В определении натурального числа ничего не говорит о природе элементов множества N. Значит, она может быть какой угодно. Стандартной моделью системы аксиом Пеано является возникший в процессе исторического развития общества ряд чисел: 1, 2, 3, 4, 5 ,.., Каждое число этого ряда имеет свое обозначение и название, которые будем считать известными. Важно заметить, что в определении натурального числа ни одну из аксиом опустить нельзя. 1 1 abcd … х у z
c b  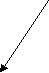 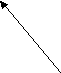  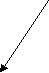 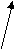  Рис. 16 Рис. 17 Задача 1. На рисунках каждый элемент соединен стрелкой со следующим за ним элементом. Установить, какие из множеств, приведенных на рисунках 15 и 16, являются моделями системы аксиом Пеано. 1. На рис. 16 изображено множество, в котором выполняются аксиомы 2 и 3, но не выполняется аксиома 1. Аксиома 4 не будет иметь смысла, так как в множестве нет элемента, непосредственно не следующего ни за каким другим. 2.На рис. 17 показано множество, в котором выполнены аксиомы 1, 2, 3, но не выполняется аксиома 4 – множество точек, лежащих на луче, содержит 1, и вместе с каждым числом оно содержит непосредственно следующее за ним число, но оно не совпадает со всем множеством точек, показанных на рисунке. Вывод: ни одно из множеств, изображенных на рис. 16 и 17, нельзя считать моделями системы аксиом Пеано. Задача 2. Докажем, что всякое натуральное число отлично от непосредственно следующего за ним натурального числа, т.е. (х )х х' Доказательство Пользуемся аксиомой индукции – А4. Пусть М= {х/х , х х'}, т.к. х М N. Доказательство состоит из двух частей.
Здесь применено правило контрапозиции (ПК), широко применяемое в доказательствах «от противного». Итак, мы получили: М N(1 М(x М => х' М)) M= N, т.е. утверждение х х' верно для любого натурального числа. Контрольные вопросы
а) новое (для учащихся) число выступает как продолжение полученного отрезка натурального ряда; б) устанавливается, что за каждым натуральным числом непосредственно следует только одно другое натуральное число. Упражнения 285. Элементами множества являются группы черточек {I, II, III, IIII,...}. Удовлетворяет ли это множество аксиомам Пеано? Как определено здесь отношение «непосредственно следовать за». Рассмотрите эти же вопросы для множества {0, 00, 000, 0000,...}. 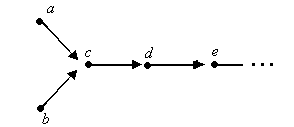 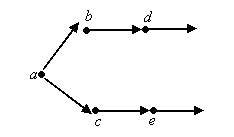 a) б) 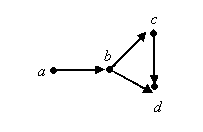 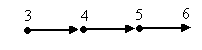 в) г) Рис. 17 286. На рисунке 17 а) каждый элемент соединен стрелкой со следующим за ним элементом. Можно ли считать множество моделью системы аксиом Пеано? Те же вопросы для множеств на рисунках 17 б), в), г). 287. Удовлетворяет ли аксиомам Пеано множество чисел {1, 2, 3 п, ...}, если отношение следования задано в нем так: 1 3 5 7…. 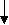 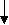 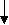 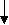 2 4 6 8…. 288. Приведите примеры заданий из учебников математики для начальных классов, в которых правильность выполнения заданий объясняется аксиомами Пеано.
___________________________________________________________________ Определение 3. Сложением натуральных чисел называется алгебраическая операция, которая каждой паре натуральных чисел а и b ставит в соответствие число вида (а + b) и обладает свойствами: 1.(а )а + 1 = а'; 2. (а, b) а + b' = (а + b)'. _____________________________________________________________________________________________ Свойства операции сложения 1 и 2 – это аксиомы и обозначим их А5 и А6. Символически это определение можно записать так: , +>, (а, b)( а, b) а + b, А5. (а ) а + 1= а' А6. (а, b)( а + b') = (а + b) '. Число а + bназывается суммой чисел а и b, а сами числа а и b – слагаемыми. Теорема 3. Сложение натуральных чисел существует и определено однозначно. Известную всем таблицу сложения однозначных чисел можно вывести, пользуясь определением сложения и теоремой о существованиииединственности сложения. Условимся о следующих обозначениях: 1' = 2; 2' = 3; 3' = 4; 4' = 5; 5' = 6; 6' = 7; 7' = 8; 8' = 9; 9' = 10. Таблица: 1) прибавление числа 1 :
… 9 + 1 2) прибавление числа 2:
… 8 + 2 = 8+1' Если продолжать этот процесс, получим всю таблицу сложения однозначных чисел. ___________________________________________________________________ Определение 4. Умножением натуральных чисел называется алгебраическая операция, которая каждой паре натуральных чисел а и b ставит в соответствие число вида а b и обладает свойствами:
______________________________________________________________________________________________ Число а bназывается произведением чисел а иb, асами числа а и b – множителями. Свойства операции умножения – это аксиомы и обозначим их А7, А8. Символически это определение можно записать так: , > (а, b)( а, b) а b. А7(а ) а 1= а А8 (а, b ) а b' = аb +a Теорема 4. Умножение натуральных чисел существует и определено однозначно. Таблицу умножения однозначных чисел можно вывести, используя определение умножения, теорему о существовании и единственности умножения и таблицу сложения. Таблица: 1. Умножение на 1: по А7(а ) а 1= а 1 1 = 1; 2 1 = 2; 3 1 = 3; 4 1 = 4; 5 1 = 5; 6 1 = 6; 7 1 =7; 8 1= 8; 9 1= 9. 2. Умножение на 2: (символическая запись т.у. – таблица умножения) 1 2=1 1' 2 2 = 2 1' 3 2 = 31' … 9 2 = 9 1' Если продолжить этот процесс, получим всю таблицу умножения однозначных чисел. Свойства операции сложения Имеют место следующие теоремы: (записаны в таком порядке, в каком их можно доказать). Для любых а, b, с из N 1. (а + b) + с = а + (b+ с) = а + b+ с; (ассоциативность) 2. а + b =b + а; (коммутативность) От перемены мест слагаемых сумма не меняется. 3. а + bbа + b а; Сумма двух любых натуральных чисел не равна ни одному из слагаемых. 4. а + b > аа + b >b; Сумма двух любых натуральных чисел больше любого из этих чисел.
а + b = а + с => b = с. (сократимость)
а + b < а + с => b< с; (монотонность) 9. а >b=> а + с >b + с; 10. а + с > b + с => а > b; а + b > а + с => b > с; (монотонность) |
