Контрольные вопросы для самоконтроля по усвоению теоретического материала, здесь же предлагается комплекс упражнений для самостоятельной работы
 Скачать 7.87 Mb. Скачать 7.87 Mb.
|
В2; В1B2 = иB1B2 = B.
Аq, n(A1) = п(А2) =...= п(Аq) = 4 = b, q – число равночисленных множеств (число столов) - надо найти.
А2
А2
…
Ab,где Аi А,i= 1,2, ..., b.
А2
В3 => п(А) = n(B1) = п(В2) = n(B3) = 2.
В1 |
Множество В – объединение множеств В1, В2 иВ3, т.е. В = В1 В2 В3, причем В1В2= , В1 В3 = , В2 В3 = , тогда n (B) = n (В1В2 В3) = п (В1) + п (В2) + п (В3) = 2 + 2 + 2 = 23 = 6. Или кратко, квадратов в 3 раза больше, чем треугольников, т.е. квадратов три раза постольку, сколько треугольников, т.е. 3 раза по 2, а это 2 + 2 + 2 = 23 = 6.
Сережа вырезал 6 квадратов.
Задача 12.
Решить и объяснить выбор действий (на смысл отношения «меньше в...» в косвенной форме).
Для урока труда девочка принесла 6 листов красной бумаги, это в 2 раза меньше, чем зеленой. Сколько листов зеленой бумаги принесла девочка?
Решение.
Красной бумаги 6 листов, это в 2 раза меньше, чем зеленой, тогда зеленой бумаги в 2 раза больше, чем красной. Пришли к задаче, аналогичной предыдущей, приводятся аналогичные рассуждения. Кратко: зеленой бумаги в 2 раза больше, чем красной, т.е. 2 раза по 6, и это можно записать 6 + 6 = 62 = 12.
Девочка принесла 12 листов зеленой бумаги.
Задача 13.
Вычислить рационально, объяснив вычисление: 7731 + 3123.
Первый способ. Можно найти значение выражения в порядке выполнения действий.
1)7731=2387; 2)3123=713; 3)2387 + 713 = 3100.
Второй способ. Можно найти значение выражения, пользуясь свойствами операций. Используя коммутативность умножения, можно поменять местами множители 77 и 31 или 31 и 23. Далее можно воспользоваться дистрибутивностью умножения относительно сложения слева или справа.
7731 + 31 23
Контрольные вопросы
Сформулируйте определение произведения целых неотрицательных чисел через декартово произведение множеств.
Сформулируйте определение произведения целых неотрицательных чисел через сумму.
Дайте определение умножения, используемое в начальном курсе математики.
Запишите свойство коммутативности умножения, дайте его теоретико-множественное истолкование.
Запишите свойство ассоциативности умножения. Приведите пример на применение этого свойства.
Запишите свойство дистрибутивности умножения относительно сложения. В каком виде используется это свойство при начальном обучении математике?
Упражнения
Используя определение произведения целых неотрицательных чисел через декартово произведение множеств, покажите, что:
а) 2 4 = 8; б)1 3 = 3; в) 0 5 = 0.
Используя определение произведения целых неотрицательных чисел через сумму, покажите, что:
а) 2 4 = 8; б) 1 3 = 3; в) 0 5 = 0.
Объясните, почему нижеприведенные задачи решаются действием умножения:
а) На каждое детское пальто нужно пришить 4 пуговицы. Сколько пуговиц нужно пришить на 7 таких пальто?
б) Юннаты посадили 3 ряда березок по 5 березок в каждом. Сколько всего березок посадили юннаты?
а) В пруду плавали 4 гуся, а уток в 3 раза больше. Сколько уток плавало в пруду?
б) В шкафу стояли 6 глубоких тарелок, а мелких в 2 раза больше. Сколько всего тарелок стояло в шкафу?
а) В цирковом представлении участвовали 6 дрессированных собачек, их было в 3 раза меньше, чем дрессированных голубей. Сколько дрессированных голубей участвовало в представлении?
б) Коля поймал 8 рыб, в 2 раза меньше, чем Женя. Сколько рыб поймали оба мальчика?
Решить разными способами:
а) Двум мальчикам раздали по 3 зеленых и по 4 красных круга каждому. Сколько всего кругов раздали этим мальчикам?
б) Для школьного зала купили новые стулья. 2 ряда по 5 стульев поставили на сцену и 8 рядов по 5 стульев поставили в зале. Сколько всего новых стульев поставили?
Вычислить рациональными способами, объяснить вычисления.
а) 319+19-27;
б) 5718 –1837;
в) 4 17 5;
г) 487525;
д) (17+ 25) 4;
е) 13156 – 3613;
ж) 1728 + 17217;
з) 2 4 17 25;
и) (53 + 35) 2;
к)1875.
Если выполняются условия:
Аi, где 1 = 1,2,...,b;
АiAj = , где i j и i, j = 1,2,...,b;
Аi А2 …b = А
И
 n(A) = с, п(А1) = n(A2) = ... = п(Аb) = а, то п(А) = п(А1)+п(А2)+...+п(Аb) = a + a+…+a = a b
n(A) = с, п(А1) = n(A2) = ... = п(Аb) = а, то п(А) = п(А1)+п(А2)+...+п(Аb) = a + a+…+a = a bb
Получаем ab = с.
Рассмотрим две задачи. В первой – по количеству элементов множества А и числу равномощных классов требуется найти число элементов в каждом из классов Аiразбиения множества. Во второй – по количеству элементов множества А и каждого из равномощных классов Аiтребуется определить количество классов разбиения.
Задача 14.
Известно: число элементов множества А, п(А) = с, число равномощных классов – b. Найти: число элементов в каждом классе, п(Аi) = а –?
Так как ab = с, то а = с : bили п(Аi) = п(А) : b, где i = 1, 2, ..., b.
Итак, частное от деления числа элементов множества А на число равномощных классов обозначает число элементов в каждом из равномощных классов.
Эта задача на деление на равные части.
Задача 15.
Известно: число элементов множества А, п (А) = с, число элементов в каждом из равномощных классов, п (Аi) = а. Найти: число классов – b.
Так как ab = с, то с : а = bили п(А):п (Аi) = b.
Итак, частное от деления числа элементов множества А на число элементов, в каждом из равномощных классов обозначает число равномощных классов.
Эта задача на деление по содержанию.
Теоретико-множественное истолкование можно дать и делению с остатком. Напомним, что разделить натуральное число а на натуральное число bс остатком – это, значит, найти такие целые неотрицательные числа q и r, что
а = bq + r, где 0 r < b.
Пусть а = п(А) и множество А разбито на множества А1, А2,... Аq, D, В так, что множества А1, А2,... Аqравночисленны, а множество Dсодержит меньше элементов, чем каждое из множеств А1, А2,... Аq.Тогда, если п(А1) = п(А2) = ...= п(Аq) = b, а п(D) = r, то а = bq+ r, где 0 r < b, причем число q(равночисленных множеств) является неполным частным при делении а на b, а число r(число элементов в D) – остатком при этом делении.
Задача 16.
Решить и объяснить выбор действий.
У бабушки было 10 морковок. Она связала их в пучки по 5 морковок в каждом. Сколько получилось пучков?
Решение:
Переведем условие и вопрос задачи на язык множеств. А – множество морковок, которые были у бабушки, п(А) = 10. А1, А2,...Аb – разбиение множества А на классы. Аi– множество морковок в каждом классе (пучке), А1
D – множество ложек, которые остались, п(D) = r – число ложек, которое надо найти.
А = (А1 А2 ...Aq) D.
п(А) = (А1 А2 ...Aq) +n(D), (А1 А2 ...Aq) D = .
а = bq+r, т.е. 13 = 4q + r.
Чтобы найти qи r, надо выполнить деление с остатком 13 на 4, 13 : 4 = 3 (ост. 1), 13 = 43 + 1.
Ложки положили на 3 стола, и одна ложка осталась.
Задача 19.
(это задача на отношение «меньше в...») Решить.
Оля нашла 8 подосиновиков, а белых грибов в 2 раза меньше. Сколько белых грибов нашла Оля?
Переведем условие и вопрос задачи на язык множеств.
А – множество подосиновиков, которые нашла Оля, п(А) = 8. В – множество белых грибов, в котором белых грибов столько же, сколько подосиновиков, В

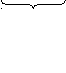 + 8 + 8 = 83 = 24
+ 8 + 8 = 83 = 24 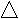
 A B
A B