ТВ. и МС.( ЧТЮ) МЕТОДИЧКА 1,2 раздел. кубанский государственный аграрный университет
 Скачать 0.88 Mb. Скачать 0.88 Mb.
|
|
3 Оценить различия в среднемесячной заработной плате механизаторов различной квалификации. Таблица 21 – Средняя месячная заработная плата механизаторов, тыс. руб.
4 Оценить существенность влияния различных сортов и доз удобрений на урожайность риса. Таблица 22 - Урожайность риса с 1га, ц
5 Оценить существенность различий уровня производительности механизаторов при культивации в различных хозяйствах по пропашным культурам и стажу работы механизаторов. Таблица 23 - Объем выполненных работ механизаторами за 1 час работы, эт. га
15 КОРРЕЛЯЦИОННО-РЕГРЕССИОННЫЙ АНАЛИЗ Корреляционно-регрессионный анализ – это совокупность статистических и математических методов, позволяющих оценить степень зависимости между результативными и факторными признаками, а также найти аналитическое выражение зависимости. Корреляционно-регрессионный анализ проводится в следующей последовательности. 1. Исходя из целей и задач исследования зависимости устанавливается результативный (У) признак и факторные (Хi) признаки. 2. По совокупности объектов определяются значения результативного и факторных признаков. 3. Обосновывается, обычно графическим методом, модель в виде уравнения регрессии. 4. Методом наименьших квадратов рассчитываются параметры уравнения регрессии. 5. Определяется теснота связи между изучаемыми признаками. 6. Оценивается значимость уравнения связи, его параметров и показателей тесноты связи. При изучении влияния одного фактора Х на изменение результативного признака У линейное уравнение регрессии имеет вид: у=а + bx. Его параметры находятся методом наименьших квадратов путем составления и решения следующей системы уравнений:  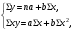 или или 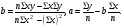 (15.1) (15.1) В линейном уравнении регрессии b 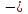 коэффициент регрессии, который показывает, на сколько единиц в среднем изменяется результативный признак Х при увеличении факторного признака У на единицу. коэффициент регрессии, который показывает, на сколько единиц в среднем изменяется результативный признак Х при увеличении факторного признака У на единицу.При линейной зависимости для оценки тесноты связи между признаками используется коэффициент корреляции: 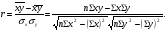 (15.2) (15.2)Статистическая гипотеза Н0 : r = 0, Н1: r 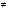 0 при уровне значимости 0 при уровне значимости 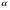 проверяется с использованием критерия Стьюдента: проверяется с использованием критерия Стьюдента: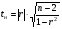 . (15.3) . (15.3)Критическое значение t находится по таблице t – Стьюдента при уровне значимости 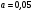 и числе степеней свободы k = n -2 для двусторонней критической области. Если и числе степеней свободы k = n -2 для двусторонней критической области. Если 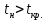 , то нулевая гипотеза отвергается, коэффициент корреляции существенно отличен от нуля в генеральной совокупности. Если , то нулевая гипотеза отвергается, коэффициент корреляции существенно отличен от нуля в генеральной совокупности. Если 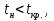 то нулевая гипотеза принимается и влияние фактора Х на У статистически не значимо. то нулевая гипотеза принимается и влияние фактора Х на У статистически не значимо. D = r2 100% 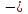 коэффициент детерминации, показывает какая часть общей колеблемости результативного признака объясняется влиянием факторного признака. коэффициент детерминации, показывает какая часть общей колеблемости результативного признака объясняется влиянием факторного признака.Э= 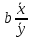 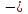 коэффициент эластичности, который показывает, на сколько процентов изменится результативный признак У, при изменении факторного признака Х на 1 %. коэффициент эластичности, который показывает, на сколько процентов изменится результативный признак У, при изменении факторного признака Х на 1 %.Теснота связи, в случае нелинейной зависимости, выраженной уравнением регрессии 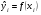 , определяется с помощью индекса (коэффициента) корреляции R: , определяется с помощью индекса (коэффициента) корреляции R: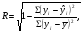 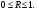 (15.4) (15.4)Значимость индекса корреляции определяется с помощью критерия F – Фишера – Снедекора при уровне значимости 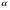 с к1 = m – числом степеней свободы числителя и к2 = (n-m-1) – числом степеней свободы знаменателя с к1 = m – числом степеней свободы числителя и к2 = (n-m-1) – числом степеней свободы знаменателя 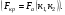 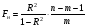 , (15.5) , (15.5)где m – число параметров уравнения регрессии, n – число наблюдений. Если Fн < Fкр, то гипотеза о том, что R не является статистически значимым отклоняется (Н0:R=0, H1:R 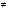 0). 0).Коэффициент эластичности в общем виде определяется по формуле: 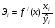 . (15.6) . (15.6)В зависимости от числа признаков, между которыми изучается связь, различают парную и множественную связь. Если изучается связь между результативным признаком, двумя и более факторными признаками, то она называется множественной связью. 1 На основании имеющихся данных определить параметры линейного уравнения регрессии между уровнем кормления и продуктивностью коров, рассчитать коэффициенты корреляции и детерминации. Оценить существенность величины коэффициентов корреляции и регрессии при уровне значимости 0,05. Таблица 24 – Уровень кормления и продуктивность коров
2 По первым 30 предприятиям, взятых из приложения 4: а) построить график зависимости между двумя признаками, определив какой из них будет результативным, а какой факторным; б) установить аналитическое выражение зависимости между признаками; в) определить методом наименьших квадратов параметры уравнения регрессии; г) оценить тесноту связи между признаками; д) при уровне значимости 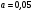 дать оценку значимости уравнения регрессии и показателей тесноты связи. дать оценку значимости уравнения регрессии и показателей тесноты связи. Зависимость изучить по следующим парам признаков: 1) площадь сельскохозяйственных угодий и валовая продукция сельского хозяйства; 2) площадь сельскохозяйственных угодий и реализованная продукция; 3) среднегодовая стоимость основных фондов и валовая продукция; 4) среднегодовая стоимость основных фондов и реализованная продукция; 5) затраты по оплате труда и валовая продукция; 6) материальные затраты и валовая продукция; 7) затраты по оплате труда и реализованная продукция; 8) энергетические мощности и валовая продукция; 9) среднегодовая численность работников предприятия и валовая продукция сельского хозяйства; 10) среднегодовая численность работников и реализованная продукция; 11) энергетические мощности и реализованная продукция; 12) затраты на производство и валовая продукция сельского хозяйства; 13) затраты на реализованную продукцию и стоимость реализованной продукции; 14) затраты на производство на 100 га сельскохозяйственных угодий и валовая продукция на 100 га сельскохозяйственных угодий; 15) затраты по оплате труда на 100 га сельхозугодий и валовая продукция на 100 га сельхозугодий; 16) затраты на реализованную продукцию на 100 га сельхозугодий и реализованная продукция на 100 га сельхозугодий; 17) среднегодовая численность работников на 100 га сельхозугодий и валовая продукция на 100 га сельхозугодий; 18) среднегодовая численность работников на 100 га сельхозугодий и реализованная продукция на 100 га сельхозугодий; 19) затраты по оплате труда на 100 га сельхозугодий и реализованная продукция на 100 га сельхозугодий. 20) затраты по оплате труда на среднегодового работник и валовая продукция на среднегодового работника; 21) энергетические мощности на среднегодового работника и реализованная продукция на работника; 22) энергетические мощности на среднегодового работника и валовая продукция на среднегодового работника; 23) энергетические мощности на 100 га сельхозугодий и валовая продукция на 100 га сельхозугодий; 24) энергетические мощности на 100 га сельхозугодий и реализованная продукция на 100 га сельхозугодий; 25) затраты по оплате труда на среднегодового работника и реализованная продукция на среднегодового работника; 26) среднегодовая стоимость основных фондов на 100 га сельхозугодий и валовая продукция на 100 га сельхозугодий; 27) среднегодовая стоимость основных фондов на 100 га сельхозугодий и реализованная продукция на 100 га сельхозугодий; 28) среднегодовая стоимость основных фондов на работника и валовая продукция на работника; 29) среднегодовая стоимость основных фондов на работника и реализованная продукция на работника; 30) материальные затраты на 100 га сельхозугодий и валовая продукция на 100 га сельхозугодий. 3 По совокупности 69 сельскохозяйственных предприятий Краснодарского края за 2007 год изучаются зависимости между результатами производства и влияющими на них факторами. Предварительные результаты по каждому признаку представлены в приложении 5, а парные коэффициенты корреляции в приложении 6. По одному варианту заданий определить: - линейные уравнения парной регрессии между результативными и факторными признаками; - значимость парных уравнений регрессии, коэффициентов регрессии и корреляции; - уравнение множественной линейной регрессии в стандартизованном и натуральном масштабе; - коэффициенты эластичности; - множественные коэффициенты корреляции и детерминации; - частные коэффициенты корреляции. Оценить статистическую значимость уравнения множественной регрессии и его параметров с помощью критериев Фишера и Стьюдента. Варианты заданий: 1) у1; х1; х2; 2) у1;х1; х3; 3) у1; х1; х4; 4) у1; х1; х5; 5) у1; х2; х3; 6) у1; х2; х4; 7) у1; х2; х6; 8) у2; х7; х8; 9) у2; х7; х9; 10) у2; х8; х9; 11) у2; х8; х10; 12) у2; х9; х10; 13) у3; х1; х2; 14) у3; х1; х3; 15) у3; х1; х4; 16) у3; х1; х5; 17) у3; х2; х3; 18) у3; х2; х4; 19) у3; х2; х6; 20) у1; х3; х6; 21) у3; х3; х6; 22) у1; х4; х5; 23) у3; х4; х5; 24) у1; х4; х6; 25) у3; х4; х6; 26) у1; х5; х6; 27) у3; х5; х6. 4 Рейтинг 9 банков был оценен тремя экспертами. С помощью коэффициента ранговой корреляции найти пары экспертов, оценки которых наиболее близко соответствует друг другу. Оценить значимость различий в оценке рейтинга банков экспертами. Таблица 25 - Рейтинг банков (номер предпочтительности)
16 АНАЛИЗ ВРЕМЕННЫХ РЯДОВ Временной ряд – это ряд значений изучаемого признака за последовательные моменты или периоды времени. Он состоит из уровней ряда (уi) и периодов или моментов времени, к которым относятся уровни (ti). Уровни ряда формируются под влиянием совокупности факторов, проявляющихся через трендовую (Т), циклическую или сезонную (S) и случайную компоненты ( 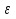 ). Применяются аддитивная У=Т+S+ε или мультипликативная У=Т∙S∙ ). Применяются аддитивная У=Т+S+ε или мультипликативная У=Т∙S∙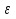 модели. модели. Для выявления во временном ряду тенденции или циклических колебаний используется коэффициент автокорреляции. Коэффициент автокорреляции уровней первого порядка, смещенных на одну единицу времени, определяется по формуле: 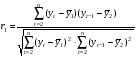 , где , где 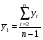 , , 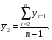 (16.1) (16.1) Для характеристики тенденций во временном ряду наиболее часто используются следующие функции: - линейная 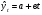 ; (16.2) ; (16.2)- степенная 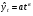 ; (16.3) ; (16.3)- гиперболическая 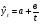 ; (16.4) ; (16.4)- показательная 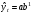 ; (16.5) ; (16.5)- полиноминальная 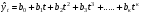 . (16.6) . (16.6)Параметры уравнений определяются методом наименьших квадратов. Для характеристики зависимости между последовательными значениями остатков применяется критерий Дарбина-Уотсона. 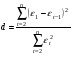 , 0 , 0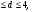 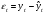 . (16.7) . (16.7)Для выявления циклических колебаний во временных рядах используется гармонический анализ. Наиболее часто применяют ряд Фурье: 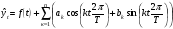 , (16.8) , (16.8)где k=1,2, …., ( 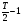 ) номер гармоники, ) номер гармоники,t = 1,2, ….., Т – номер интервала или момента времени, Т – число уровней временного ряда, 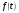 - выравненный уровень в момент или интервал времени t. - выравненный уровень в момент или интервал времени t.Если в исходном временном ряду тенденции развития не обнаружено, то 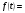 а0. а0.Параметры ряда Фурье определяются методом наименьших квадратов по формулам: 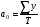 , , 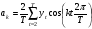 , , 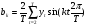 . (16.9) . (16.9)Если в исходном ряду обнаружена тенденция и найдены значения 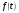 , то в формуле (16.8) вместо уt , используется , то в формуле (16.8) вместо уt , используется 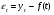 . .
Таблица26 - Урожайность сельскохозяйственных культур с 1 га, ц
2 Имеются следующие данные об объеме подрядных работ строительной организации Таблица 27 - Объем подрядных работ, млн. руб.
Построить график динамики объема подрядных работ. Определить параметры тренда объема подрядных работ, включающего общую закономерность изменения объема работ и периодическую составляющую, используя периодическую функцию ряда Фурье. ОТВЕТЫ РАЗДЕЛ 1
РАЗДЕЛ 2
РАЗДЕЛ 3
РАЗДЕЛ 4
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

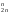
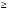 40867.
40867.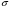 (Z)=0,87
(Z)=0,87