ТВ. и МС.( ЧТЮ) МЕТОДИЧКА 1,2 раздел. кубанский государственный аграрный университет
 Скачать 0.88 Mb. Скачать 0.88 Mb.
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Стаж работы, лет | До 1 | 1-5 | 5-10 | 10-20 | 20-40 | Всего |
| Число работников,чел. | 8 | 22 | 46 | 34 | 10 | 120 |
Найти средний стаж работы, среднее квадратическое отклонение и коэффициент вариации.
Путем устного опроса изучалось качество продукции, выпускаемой фирмой и реализуемой в магазине этой фирмы. Посетители давали оценку качества по десятибалльной шкале.
Таблица 2- Бальная оценка продукции предприятия
| Оценка качества продукции, балл | 1-2 | 3-4 | 5-6 | 7-8 | 9-10 |
| Число случаев | 3 | 8 | 36 | 89 | 45 |
Определить средний балл качества продукции, среднее квадратическое
отклонение, коэффициент вариации, показатели асимметрии и эксцесса.
Имеются следующие данные о площади посева овощей в хозяйствах
по совокупности районов.
Таблица 3 - Площадь посева овощей на хозяйство, га
| Район | Номер хозяйства | ||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 1 | 8 | 10 | 12 | 6 | 15 | 30 | 21 |
| 2 | 32 | 16 | 26 | 41 | 44 | 38 | - |
| 3 | 101 | 65 | 96 | 144 | 84 | 76 | 90 |
| 4 | 22 | 30 | 44 | 18 | 16 | 31 | - |
| 5 | 10 | 7 | 4 | 3 | 12 | 7 | 6 |
| 6 | 25 | 36 | 38 | 27 | 45 | 51 | - |
| 7 | 121 | 84 | 96 | 110 | 161 | 143 | - |
| 8 | 34 | 16 | 84 | 71 | 36 | 8 | 17 |
| 9 | 46 | 41 | 48 | 52 | 50 | 58 | - |
| 10 | 15 | 24 | 86 | 144 | 34 | 14 | 24 |
Дать сравнительную оценку колеблемости площади посева овощей в хозяйствах двух районов.
По данным распределения студентов по результатам сдачи экзаменов
определить: а) средний балл успеваемости студентов по каждому предмету и по всем предметам; б) дисперсии балла успеваемости по предмету и в целом по всем предметам; в) межгрупповую дисперсию. Найти общую дисперсию успеваемости, используя правило сложения дисперсий.
Таблица 4 - Распределение студентов группы по результатам сдачи
экзаменов
| Оценка | Число студентов, получивших оценку по предметам | |||
| 1 | 2 | 3 | 4 | |
| 2 | 2 | 1 | 4 | 3 |
| 3 | 6 | 10 | 8 | 8 |
| 4 | 10 | 8 | 9 | 9 |
| 5 | 7 | 6 | 4 | 5 |
8 Работники предприятия сгруппированы по возрасту.
Таблица 5 - Распределение работников предприятия по возрасту
| Категория работников | Возраст работников, лет | Всего | ||||
| До 30 | 30-40 | 40-50 | 50-60 | свыше 60 | работников | |
| Рабочие | 43 | 141 | 216 | 127 | 52 | 579 |
| Руководители | 2 | 4 | 6 | 8 | 4 | 24 |
| Специалисты | 3 | 18 | 30 | 34 | 12 | 97 |
| Всего работников | 48 | 163 | 252 | 169 | 68 | 700 |
Определить: а) средний возраст работников предприятия в целом и по категориям: б) модальное и медианное значения возраста работников по категориям и предприятию; в) дисперсию и среднее квадратическое отклонение возраста по категориям работников и предприятию; г) межгрупповую дисперсию возраста работников. Найти общую дисперсию возраста работников, используя правило сложения дисперсий.
12 ВЫБОРОЧНЫЙ МЕТОД
Выборочным называется наблюдение, при котором обследованию подвергается часть единиц совокупности, отобранных на основе научно разработанных принципов, а показатели, найденные по отобранной части единиц, должны достаточно точно характеризовать всю совокупность единиц.
Совокупность единиц, из которой производится отбор, называется генеральной совокупностью, а ее часть, подвергающаяся изучению
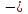 выборочной совокупностью. Отбор единиц из генеральной совокупности может быть произведен повторным или бесповторным способом. Если отобранная единица возвращается в генеральную совокупность и может снова попасть в выборку, то отбор
выборочной совокупностью. Отбор единиц из генеральной совокупности может быть произведен повторным или бесповторным способом. Если отобранная единица возвращается в генеральную совокупность и может снова попасть в выборку, то отбор 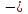 повторный. Если же отобранная единица в генеральную совокупность не возвращается, то отбор – бесповторный.
повторный. Если же отобранная единица в генеральную совокупность не возвращается, то отбор – бесповторный. Генеральная доля
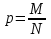
 , выборочная доля, w =
, выборочная доля, w = 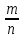 . где М и m – число единиц генеральной и выборочной совокупности, обладающих определенным свойством; N и n – объемы генеральной и выборочной совокупности соответственно.
. где М и m – число единиц генеральной и выборочной совокупности, обладающих определенным свойством; N и n – объемы генеральной и выборочной совокупности соответственно. Отбор единиц производится случайным, механическим, типическим, серийным, комбинированным и другими способами.
Случайным называется отбор единиц из генеральной в выборочную совокупность, при котором каждая единица имеет одинаковую вероятность попасть в выборку. Основной задачей выборочного метода является количественная оценка параметров генеральной совокупности по данным выборки. Для того, чтобы статистические оценки давали «хорошие» приближения оцениваемых параметров генеральной совокупности по выборке, они должны обладать свойствами несмещенности, эффективности и состоятельности.
Оценка параметров генеральной совокупности может быть точечной и интервальной. Точечная оценка задается одним числом. Оценка, задаваемая двумя числами (границами интервала), называется интервальной.
Доверительный интервал рассчитывается по формуле:
для доли
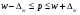 ; (12.1)
; (12.1)для средней
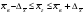 , (12.2)
, (12.2)где
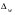 и
и 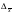 - предельные ошибки выборки для доли и средней соответственно.
- предельные ошибки выборки для доли и средней соответственно. Таблица 6 - Формулы расчета предельной ошибки выборки при
случайном отборе
| Предельная ошибка | Повторный отбор | Бесповторный отбор |
| Для средней | 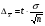 | 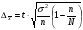 |
| Для доли | 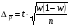 | 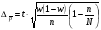 |
В больших выборках (n > 60) t находится по таблице значений функций Ф (х) при заданном уровне доверительной вероятности
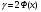 . Если
. Если 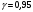 , t=1,96; если
, t=1,96; если 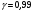 , t=2,58.
, t=2,58. В малых выборках
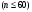 t находится по таблице t- распределения Стьюдента в соответствии с заданным уровнем доверительной вероятности
t находится по таблице t- распределения Стьюдента в соответствии с заданным уровнем доверительной вероятности 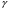 и числом степеней свободы k = n – 1. Оценка генеральной дисперсии служит «исправленная» выборочная дисперсия:
и числом степеней свободы k = n – 1. Оценка генеральной дисперсии служит «исправленная» выборочная дисперсия: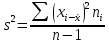 . (12.3)
. (12.3)Таблица 7 - Формулы расчета необходимой численности выборки при
случайном отборе
| Предельная ошибка | Повторный отбор | Бесповторный отбор |
| Для средней | 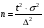 | 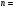 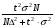 |
| Для доли | 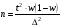 | n= 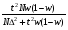 |
1 Для определения потерь зерна при уборке случайным способом проведено 100 измерений. Средняя величина потерь составила 1,8 ц с одного гектара посевов, при среднем квадратическом отклонении 0,5 ц с га. С доверительной вероятностью 0,95 определить границы, в которых будет находиться средняя величина потерь зерна с 1 га и возможная величина потерь, если площадь уборки зерновых составила 640 га.
2 С помощью случайной выборки изучалось время выполнения производственной операции рабочими бригады. На основании 60 наблюдений установлено, что в среднем на выполнение производственной операции затрачивалось 0,5 часа, при среднем квадратическом отклонении 0,12часа. Считая время выполнения производственной операции нормально - распределенной случайной величиной, определить границы, в которых находится среднее время выполнения производственной операции всех рабочих с доверительной вероятностью :
а) 0,9; б) 0,95.
3 Случайным бесповторным способом изучались остатки горюче-смазочных материалов на складе предприятий. Обследовано 110 предприятий из 750. Средние остатки составили 150 т, при среднем квадратическом отклонении 42 т. С доверительной вероятностью 0,95 определить границы, в которых будут находиться средние остатки горюче-смазочных материалов на одно предприятие и общие остатки горюче-смазочных материалов.
4 Считая данные задачи 1 темы 11 результатом 20% выборки, определить: а) несмещенные оценки математического ожидания, дисперсии и среднего квадратического отклонения разряда рабочих; б) доверительный интервал для математического ожидания с доверительной вероятностью 0,95; в) вероятность того, что интервал (0,95
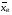 ; 1,05
; 1,05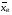 ) покроет математическое ожидание разряда рабочего; г) объем выборки, при котором с доверительной вероятностью 0,95 предельная ошибка выборки уменьшится в 1,5 раза, при сохранении значений остальных характеристик.
) покроет математическое ожидание разряда рабочего; г) объем выборки, при котором с доверительной вероятностью 0,95 предельная ошибка выборки уменьшится в 1,5 раза, при сохранении значений остальных характеристик. 5 Считая данные задачи 2 темы 11 результатом 20% выборки, определить: а) несмещенные оценки математического ожидания, дисперсии и среднего квадратического отклонения числа производственных рабочих в расчете на одно крестьянское (фермерское) хозяйство; б) доверительный интервал для математического ожидания с доверительной вероятностью 0,9; в) объем выборки, при котором с доверительной вероятностью 0,9 предельная ошибка выборки уменьшится в 2 раза, при сохранении значений остальных характеристик.
6 Считая данные задачи 3 темы 11 результатом 20% случайной бесповторной выборки, определить: а) несмещенные оценки математического ожидания, дисперсии и среднего квадратического отклонения изучаемого параметра; б) доверительный интервал для математического ожидания с доверительной вероятностью 0,95; в) вероятность того, что интервал (0,95
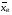 ; 1,05
; 1,05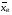 ) покроет математическое ожидание изучаемого параметра; г) объем выборки, при котором с доверительной вероятностью 0,95 предельная ошибка выборки уменьшится в 2 раза, при сохранении значений остальных характеристик.
) покроет математическое ожидание изучаемого параметра; г) объем выборки, при котором с доверительной вероятностью 0,95 предельная ошибка выборки уменьшится в 2 раза, при сохранении значений остальных характеристик.7 В районе имеется 10000 дачных участков населения. В результате выборочного обследования 300 дачных участков оказалось, что средняя выборочная урожайность овощей составила 250 ц с гектара при среднем квадратическом отклонении 60 ц с га. Известно, что 40% общей площади посевов овощей занимали помидоры. С доверительной вероятностью 0,95 определить границы, в которых будет находиться средняя урожайность овощей на всех дачных участках и удельный вес посевов помидор. Сколько необходимо обследовать дачных участков, чтобы предельная ошибка выборки по признакам уменьшилась в 1,5 раза?
8 Для определения влажности зерна случайным способом было взято 25 проб. Средний процент влажности зерна составил 16%, а выборочное среднее квадратическое отклонение 2,5%. Определить: а) несмещенные оценки математического ожидания, дисперсии и среднего квадратического отклонения; б) интервал, который покроет математическое ожидание с доверительной вероятностью, 0,95.
9 Вероятность изготовления продукции высшего качества фирмой составляет 0,9. Сколько необходимо обследовать единиц продукции, чтобы с доверительной вероятностью 0,95 можно было утверждать, что доля продукции высшего качества по выборке будет отклоняться от постоянной вероятности по модулю не более чем на 0,03?
10 Случайным бесповторным способом проведено выборочное обследование семей района. Из 1300 семей обследовано 130, по которым определен душевой доход на члена семьи, представленный в виде интервального вариационного ряда.


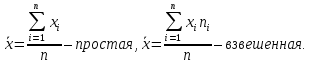 ( 8.2)
( 8.2)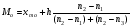 ; (8.3)
; (8.3)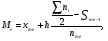 (8.4)
(8.4)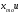
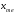 - нижняя граница модального и медиального интервалов;
- нижняя граница модального и медиального интервалов;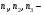 соответственно частота предмодального, модального и послемодального интервалов;
соответственно частота предмодального, модального и послемодального интервалов;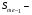 накопленная частота интервала, предшествующего медианному интервалу.
накопленная частота интервала, предшествующего медианному интервалу.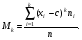 (8.5)
(8.5)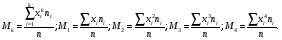 (8.6)
(8.6)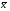 , то момент называется центральным
, то момент называется центральным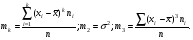 (8.7)
(8.7)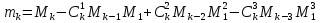 +…
+…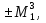 (8.8)
(8.8)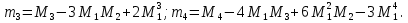 (8.9
(8.9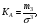 ( 8.10)
( 8.10)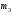 - центральный момент третьего порядка.
- центральный момент третьего порядка.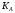 = 0, то вариационный ряд является симметричным;
= 0, то вариационный ряд является симметричным;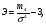 (8.11)
(8.11) 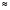 0, то распределение средневершинное;
0, то распределение средневершинное; 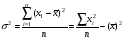
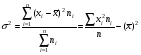 - взвешенная. (8.13)
- взвешенная. (8.13)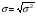 . (8.14)
. (8.14) 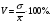 (8.15)
(8.15)