1 СЛУЧАЙНЫЕ СОБЫТИЯ
Событие есть возможный результат опыта или испытания.
Достоверным называется событие U, которое в данном опыте обязательно произойдет.
Невозможным называется событие V, которое в данном опыте не может произойти.
Случайным называется событие А, которое в данном опыте или испытании может произойти, а может и не произойти.
События называются совместными, если появление одного из них не исключает появление других в данном опыте. Если два события не могут появиться в одном опыте, то они называются несовместными.
Несколько событий называются попарно-несовместными, если никакие два из них не могут появиться вместе в данном опыте.
Совокупность несовместных и единственно возможных событий образуют полную группу событий.
События являются равновозможными, если имеются основания считать, что ни одно из них не является более возможным, чем другое.
Вероятность события А обозначается Р(А) и находится по формуле:
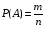 , (1.1) , (1.1)
где 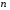 - общее число элементарных исходов (событий) в опыте или испытании; - общее число элементарных исходов (событий) в опыте или испытании;
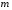 - число элементарных исходов (событий), благоприятствующих появлению события А. - число элементарных исходов (событий), благоприятствующих появлению события А.
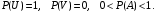 (1.2) (1.2)
где U – достоверное событие; V – невозможное событие; A – случайное событие.
Вероятность любого события А заключена между нулем и единицей,
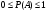 . (1.3) . (1.3)
При определении вероятностей событий часто используются формулы комбинаторики, позволяющие подсчитать число различных способов выбора 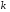 элементов из элементов из 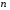 элементного множества по схеме без возвращений и с возвращениями: элементного множества по схеме без возвращений и с возвращениями:
- число размещений из 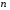 элементов по элементов по 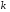 элементов без возвращений элементов без возвращений
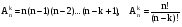 ; (1.4) ; (1.4)
- число перестановок из 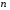 элементов элементов
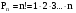 ; (1.5) ; (1.5)
- число сочетаний из 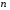 элементов по k элементовбез возвращений элементов по k элементовбез возвращений
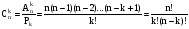 . (1.6) . (1.6)
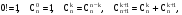 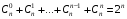 . .
Различные размещения отличаются друг от друга или порядком или составом. Различные сочетания отличаются друг от друга только составом. Перестановки отличаются порядком своих элементов.
Число перестановок, размещений и сочетаний с возвращениями определяется по формулам:
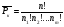 ; n1 + n2 + … + nm = n; ; n1 + n2 + … + nm = n; 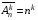 ; ; 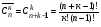 (1.7) (1.7)
Относительной частотой или статистической вероятностью события А называется число исходов, в которых появилось событие А к общему числу проведенных исходов.
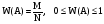 . (1.8) . (1.8)
Если число элементарных исходов бесконечно, то используют геометрическое определение вероятности.
Вероятность попадания точки в область 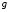 , брошенной в область , брошенной в область 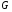 равна отношению меры ( равна отношению меры (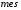 )области )области 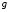 к мере области к мере области 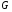 . .
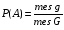 . (1.9) . (1.9)
1Являются ли несовместными следующие события:
а) Опыт - бросание двух монет; события:
А1 – появление двух гербов; А2 – появление двух цифр.
б) Опыт – три выстрела по мишени; события:
В1 – хотя бы одно попадание; В2 – хотя бы один промах.
в) Опыт – бросание двух игральных костей; события:
С1 – хотя бы на одной кости появилось три очка;
С2 – появление четного числа очков на каждой кости.
г) Опыт – извлечение двух шаров из урны, содержащей белые и
черные шары; события:
Д1 – взято два белых шара; Д2 – оба извлеченных шара одного цвета.
д) Опыт – студент сдает три экзамена, события:
Е1 – студент сдает хотя бы один экзамен;
Е2 – студен не сдает хотя бы один экзамен;
е) Опыт – лифт отправляется с 10 пассажирами и останавливается
на пяти этажах; события:
F1 – на первых четырех остановках вышло не более 9 человек;
F2 – на последней остановке вышел хотя бы один человек.
2 Образуют ли полную группу следующие события:
а) Опыт – два выстрела по мишени; события:
А1 – два попадания в мишень; А2 – хотя бы один промах по мишени.
б) Опыт – бросание двух игральных костей; события:
В1 – сумма очков на верхних гранях больше 3;
В2 – сумма очков на верхних гранях равна 3.
в) Опыт – посажено четыре зерна; события:
С1 – взошло одно зерно; С2 – взошло два зерна;
С3 – взошло три зерна; С4 – взошло четыре зерна.
г) Покупатель посещает три магазина; события:
Д1 – покупатель купит товар хотя бы в одном магазине;
Д2 – покупатель не купит товар ни в одном магазине.
д) Опыт – студент сдает три экзамена; события:
Е1 – студент сдаст хотя бы один экзамен;
Е2 – студент не сдаст хотя бы один экзамен.
3 Являются ли равновозможными следующие события:
а) Опыт – выстрел по мишени; события:
А1 – попадание при выстреле; А2 – промах при выстреле.
б) Опыт – бросание двух игральных костей; события:
В1 – произведение очков на верхних гранях равно 12;
В2 – сумма очков на верхних гранях равна 9.
в) Бросание двух монет; события:
С1 – появление двух гербов; С2 – появление двух цифр;
С3 – появление одного герба и одной цифры.
г) Опыт – извлечение двух карт из колоды; события:
Д1 – обе карты одинаковой масти;
Д2 – обе карты разных мастей.
4 Брошены 3 монеты.
Составить события, образующие полную группу.
Сколько равновозможных исходов образует полную группу событий?
Укажите события единственно – возможные, не образующие полной группы событий?
Приведите примеры:
а) трех событий, образующих полную группу событий;
б) трех событий, равновозможных и несовместных, но не образующих полной группы событий;
в) двух событий, несовместных и образующих полную группу событий, но не равновозможных.
Брошена игральная кость. Найти вероятность того, что на ее верхней грани появится: а) шесть очков; б) нечетное количество очков; в) не менее четырех очков; г) не более двух очков; д) более трех очков.
Набирая номер телефона, абонент забыл две цифры и, помня лишь, что они различны, набрал их наудачу. Найти вероятность того, что набраны нужные цифры.
Брошены две игральные кости. Найти вероятность того, что:
а) на обеих костях появится одинаковое число очков;
б) хотя бы на одной кости появится два очка;
в) сумма выпавших очков равна пяти, а произведение шести очкам;
г) сумма очков, выпавших на обеих костях, не превзойдет 5.
Из 10150 человек, проживающих в населенном пункте, 71 человек имеет возраст свыше 80 лет. Определить статистическую вероятность появления лиц с возрастом свыше 80 лет. Какой процент лиц, имеет возраст до 80 лет?
Относительная частота (частость) работников предприятия, имеющих высшее образование, равна 0.15. Определить: а) число работников, имеющих высшее образование, если всего на предприятии работает 40 человек; б) число работников предприятия, если с высшим образованием работает 30 человек.
Имеются две урны. В первой – 10 красных и 6 черных шаров. Во второй – 4 красных и 6 черных шаров. Из каждой урны вынимается по шару. Найти вероятность того, что: а) оба шара будут красными; б) из первой урны будет вынут красный шар, а из второй – черный; в) хотя бы один из вынутых шаров черный.
Из коробки, содержащей 5 пронумерованных жетонов, вынимают один за другим все находящиеся в ней жетоны и укладывают рядом. Найти вероятность того, что номера вынутых жетонов будут идти по порядку 1, 2, 3, 4, 5.
Из пяти букв разрезной азбуки составлено слово «книга». Ребенок, не умеющий читать, рассыпал эти буквы, а затем собрал в произвольном порядке. Найти вероятность того, что у него снова получилось слово «книга».
В колоде 36 карт четырех мастей. После извлечения и возвращения одной карты, колода перемешивается и снова извлекается одна карта. Определить вероятность того, что обе извлеченные карты одной масти.
На отдельных одинаковых карточках написаны цифры: 1, 2, 3, 4, 5, 6, 7, 8, 9. Все девять карточек перемешивают, после чего наугад берут четыре карточки и раскладывают в ряд в порядке появления. Какова вероятность получить при этом: а) четное число; б) число 1234; в) 6789?
Какова вероятность, что на трех карточках, вынутых по одной и положенных в порядке их появления, получим число 325, если всего карточек было шесть с цифрами 1, 2, 3, 4, 5, 6?
Восемь различных книг расставляются наугад на полке. Найти вероятность того, что: а) три определенные книги окажутся поставленными рядом; б) две определенные книги окажутся поставленными рядом.
Среди изготовленных 15 деталей имеется 5 нестандартных. Определить вероятность того, что взятые наугад три детали окажутся стандартными.
В партии готовой продукции из 10 изделий имеется 7 изделий повышенного качества. Наудачу отбираются шесть изделий. Какова вероятность того, что четыре из них будут повышенного качества?
Какова вероятность того, что два определенных студента будут посланы на практику в Лабинск, если предоставлено 6 мест в г. Лабинск, 10 – в г. Анапу и 4 – в г. Тимашевск?
Из 25 студентов группы, 12 занимаются научной работой на кафедре бухгалтерского учета, 7 - экономического анализа, остальные – на кафедре статистики. Какова вероятность того, что два случайно отобранных студента занимаются научной работой на кафедре статистики?
Собрание, на котором присутствует 25 человек, в том числе 5 женщин, выбирает делегацию из трех человек. Найти вероятность того, что в делегацию войдут: а) две женщины и один мужчина; б) все женщины.
Среди 20 студентов группы, в которой 10 девушек, разыгрываются 5 билетов в театр. Определить вероятность того, что среди обладателей билетов окажутся три девушки или две девушки.
Определить вероятность того, что участник лотереи «Спортлото – 5 из 36» угадает правильно: а) все 5 номеров; б) 3 номера.
Цифровой замок содержит на общей оси 4 диска, каждый из которых разделен на 6 секторов, отмеченных цифрами. Замок открывается в том случае, если диски установлены так, что цифры на них составляют определенное четырехзначное число. Какова вероятность того, что замок откроется, если установить произвольную комбинацию цифр?
Устройство состоит из пяти элементов, из которых два изношены. При включении устройства включается случайным образом два элемента. Найти вероятность того, что включенными окажутся неизношенные элементы.
В коробке пять одинаковых изделий, причем три из них окрашены. Наудачу извлечены два изделия. Найти вероятность того, что среди двух извлеченных изделий окажутся: а) одно окрашенное изделие; б) два окрашенных изделия; в) хотя бы одно окрашенное изделие.
В квадрат с длиной стороны «а» вписан круг. Наудачу в квадрат бросается точка. Найти вероятность того, что точка попадает в круг.
В прямоугольник с вершинами А (1;1), В (1;3), С (4;3), Д (4;1) наудачу брошена точка К (х;у). Найти вероятность того, что координаты этой точки удовлетворяют неравенству 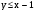 . .
В прямоугольник с вершинами А (0;0), В (0;5), С (6;5), Д (6;0) наудачу брошена точка. Найти вероятность того, что координаты этой точки удовлетворяют системе неравенств 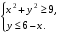
2 ОСНОВНЫЕ ТЕОРЕМЫ И ИХ СЛЕДСТВИЯ
Теорема сложения вероятностей несовместных событий. Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий:
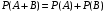 . (2.1) . (2.1)
Для n несовместных событий теорема имеет вид:
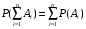 . (2.2) . (2.2)
Следствие 1. Сумма вероятностей несовместных событий, образующих полную группу событий, равна 1.
Следствие 2. Сумма вероятностей противоположных событий равна 1:
 или p + q = 1. (2.3) или p + q = 1. (2.3)
Теорема сложения вероятностей совместных событий. Вероятность суммы двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:
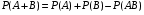 . (2.4) . (2.4)
События называются независимыми, если появление одного из них не изменяет вероятности появления другого события.
Теорема умножения вероятностей независимых событий. Вероятность совместного появления двух или нескольких независимых событий равна произведению вероятностей этих событий:
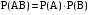 ; ; 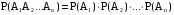 . (2.5) . (2.5)
Теорема умножения вероятностей зависимых событий. Вероятность произведения двух зависимых событий равна произведению вероятности наступления первого события на условную вероятность второго события при условии, что первое событие уже наступило:
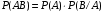 ; (2.6) ; (2.6) 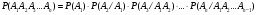 . (2.7) . (2.7)
Теорема наступления хотя бы одного из событий. Вероятность наступления хотя бы одного из событий А1, А2, …, Аn, независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий 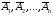 : :
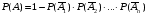 . (2.8) . (2.8)
Следствие. Если события Аi имеют одинаковую вероятность появиться р, то вероятность появления хотя бы одного события из n независимых событий:
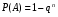 , где р + q = 1. (2.9) , где р + q = 1. (2.9)
Формула полной вероятности. Пусть событие А может появиться вместе с одним из попарно несовместных событий 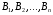 образующих полную группу событий. Будем называть события образующих полную группу событий. Будем называть события 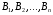 гипотезами для события А. Тогда вероятность наступления события А определяется по формуле: гипотезами для события А. Тогда вероятность наступления события А определяется по формуле:
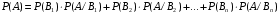 , (2.10) , (2.10)
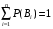 . (2.11) . (2.11)
Следствие. Условная вероятность наступления события Вi , при условии, что событие А уже произошло, определяется по формуле Байеса:
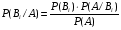 , (2.12) , (2.12)
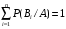 , (2.13) , (2.13)
где 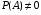 - находится по формуле полной вероятности. - находится по формуле полной вероятности.
Производится три выстрела по мишени. Рассматриваются события: А1 – попадание в цель первым выстрелом; А2 – попадание в цель вторым выстрелом; А3 – попадание в цель третьим выстрелом. Определить, каким событиям равносильны следующие события: 1) 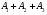 ; 2) ; 2) 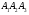 ; ;
3) 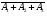 ; 4) ; 4) 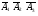 ; 5) ; 5)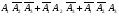 ; 6) ; 6) 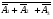 ; ;
7) 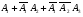 ; 8) ; 8) 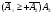 ; 9) ; 9) 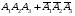 . .
Монета подбрасывается три раза. Рассматриваются события Аi – появление герба при – появление герба при 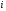 – ом подбрасывании – ом подбрасывании 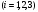 . Представить в виде сумм, произведений и сумм произведений событий Ai и . Представить в виде сумм, произведений и сумм произведений событий Ai и 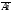 следующие события: следующие события: 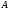 - появились все три герба; - появились все три герба; 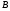 - появились все три цифры; - появились все три цифры; 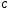 - появился хотя бы один герб; - появился хотя бы один герб; 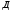 - появилась хотя бы одна цифра; - появилась хотя бы одна цифра; 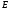 - появился только один герб; - появился только один герб; 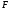 - появилась только одна цифра. - появилась только одна цифра.
Круговая мишень состоит из трех зон. Вероятности попадания в эти зоны при одном выстреле соответственно равны 0,1; 0,35 и 0,4. Найти вероятность: а) попадания в первую или третью зоны; б) промаха по мишени.
Вероятность поражения первой мишени для данного стрелка равна 0,6. Если при первом выстреле зафиксировано попадание, то стрелок получает право на следующий выстрел по второй мишени. Вероятность поражения обеих мишеней при двух выстрелах равна 0,3. Определить вероятность поражения второй мишени.
В группе 25 студентов, из них 10 юношей и 15 девушек. Какова вероятность того, что из отобранных наудачу трех студентов: а) все три девушки; б) первые две девушки, третий - юноша; в) все три юноши?
Вероятность попадания в цель при одном выстреле равна 0,7. Выстрелы производятся по одному до первого попадания. Определить вероятность того, что придется производить четвертый выстрел.
Вероятность безотказной работы автомобиля равна 0,9. Автомобиль осматривается двумя механиками. Вероятность того, что первый механик обнаружит неисправность равна 0,8, а второй – 0,9. Если хотя бы один механик обнаружит неисправность, то автомобиль отправляется в ремонт. Найти вероятность того, что: а) автомобиль будет выпущен на линию; б) автомобиль не будет выпущен на линию.
Вероятность одного попадания в цель при одновременном залпе из двух орудий 0,38. Найти вероятность поражения цели при одном выстреле первым орудием, если для второго орудия эта вероятность равна 0,8.
Из 40 деталей в ящике 5 бракованных. Какова вероятность того, что взятые наудачу две детали не будут бракованными?
В коробке 12 карандашей трех цветов, по четыре карандаша каждого цвета. Наудачу последовательно вынимают три карандаша. Найти вероятность того, что все карандаши окажутся разного цвета. Решить задачу при условии: а) карандаши возвращают в коробку; б) карандаши не возвращают в коробку.
Из урны, содержащей четыре красных и шесть черных шаров, вынимают два шара (без возвращения первого). Какова вероятность того, что будут вынуты: а) оба шара черного цвета; б) красный и черный в любой последовательности; в) второй шар будет черным; г) оба шара одного цвета?
Вероятность выигрыша по лотерейному билету равна 0,1. Приобретено три билета. Какова вероятность выиграть хотя бы по одному из них?
Вероятность попадания в цель при стрельбе из орудия равна 0,6. Производится по одному выстрелу одновременно из трех орудий. Цель будет поражена, если в нее попадут не менее двух орудий. Найти вероятность: а) поражения цели; б) промаха одним или двумя орудиями.
Слово «машина» составлено из букв разрезной азбуки. Какова вероятность того, что перемешав буквы и укладывая их в ряд по одной, получим слово: а) «машина»; б) «шина»; в) «маша»?
В магазин вошли три покупателя. Вероятность того, что каждый что-нибудь купит, равна 0,3. Найти вероятность того, что: а) два из них совершат покупки; б) все три совершат покупки; в) ни один не совершит покупки; г) по крайней мере два совершат покупки; д) хотя бы один купит товар.
Вероятность получить высокие дивиденды по акциям на первом предприятии – 0,2, на втором – 0,35, на третьем – 0,15. Определить вероятность того, что акционер, имеющий акции всех предприятий, получит высокие дивиденды: а) на всех предприятиях; б) только на одном предприятии; в) хотя бы на одном предприятии.
В продаже имеется 12 акций одного предприятия, 8 другого и 10 третьего. Клиент покупает три акции. Найти вероятность того, что клиентом будут куплены: а) акции одного предприятия; б) все три акции разных предприятий.
Два игрока поочередно бросают игральную кость. Выигрывает тот, у которого первым появится шесть очков. Найти вероятность выигрыша для каждого игрока.
Через автобусную остановку проходят автобусы семи маршрутов с равной частотой. Пассажир ожидает автобус одного из маршрутов №1, №5, №7. Какова вероятность, что нужный ему автобус будет одним из первых трех подошедших к остановке?
Читатель в поисках нужной книги обходит три библиотеки. Вероятность того, что она имеется в очередной библиотеке равна 0,3. Что вероятнее – найдет читатель книгу или нет?
В денежно-вещевой лотерее на каждые 1000 билетов приходится 12 денежных и 8 вещевых выигрышей. Какова вероятность выигрыша хотя бы на один из трех приобретенных билетов?
В урне 10 красных, 5 зеленых и 3 черных шара. Определить вероятность того, что взятые наудачу два шара будут: а) одного цвета; б) разных цветов.
На базу поступило 40 ящиков овощей, из них 30 первого сорта. Наудачу для проверки берут два ящика. Какова вероятность, что оба содержат овощи: а) первого сорта; б) разного сорта; в) одного сорта?
Читатель разыскивает книгу в трех библиотеках. Одинаково вероятно, есть или нет в фонде очередной библиотеки книга и также одинаково вероятно, выдана она или нет. Чему равна вероятность того, что читатель найдет нужную книгу?
Три студента сдают экзамен. Вероятность того, что отдельный студент сдаст экзамен на «отлично» равна для первого студента 0,7, для второго - 0,6, для третьего – 0,2. Какова вероятность того, что экзамен будет сдан на «отлично»: а) одним студентом; б) двумя студентами; в) хотя бы одним; г) ни одним?
Первый студент из 20 вопросов программы выучил 17, второй – 12. Каждому студенту задают по одному вопросу. Определить вероятность того, что: а) оба студента правильно ответят на вопрос; б) хотя бы один ответит верно; в) правильно ответит только первый студент.
Сколько раз необходимо бросить игральную кость, чтобы с вероятностью 0,9 хотя бы один раз выпало не менее четырех очков?
В первой бригаде 6 тракторов, во второй – 9. В каждой бригаде один трактор требует ремонта. Из каждой бригады наудачу выбирают по одному трактору. Какова вероятность того, что: а) оба трактора исправны; б) один требует ремонта; в) трактор из второй бригады исправен.
На предприятии имеется три автомобиля. Вероятность безотказной работы первого из них равна 0,9, второго – 0,7, третьего – 0,8. Найти вероятности всех возможных значений числа автомобилей, работающих безотказно в течение определенного времени.
Вероятность хотя бы одного попадания в мишень стрелком при трех выстрелах равна 0,784. Найти вероятность одного промаха при трех выстрелах.
В круг радиуса R вписан прямоугольник наибольшей площади. Чему равна вероятность того, что поставленные наудачу внутри круга две точки окажутся внутри заданного прямоугольника?
В шар радиуса R вписан прямой конус наибольшего объема. Чему равна вероятность того, что из поставленных наудачу внутри шара двух точек хотя бы одна окажется внутри конуса.
Вероятность спортсменом взять в одной попытке высоту 1,8 м равна 0,6, высоту 2 м – 0,2, высоту 2 м 10 см – 0,1. Спортсмен, не взявший предыдущую высоту, выбывает из соревнований. Спортсмену на каждую высоту дается три попытки. Определить вероятность того, что спортсмен закончит соревнования, взяв высоту: а) 1,8 м; б) 2 м; в) 2 м 10 см.
В первой урне 5 красных, 3 белых и 2 черных шара. Во второй 3 белых и 2 черных шара. Из первой урны взято 2 шара, а из второй один. Определить вероятность того, что среди них: а) все шары одного цвета; б) все шары разного цвета.
При исследовании жирности молока коров все стадо было разбито на три группы. В первой группе оказалось 70%, во второй 23% и в третьей 7% всех коров. Вероятность того, что молоко, полученное от отдельной коровы, имеет не менее 4% жирности, для каждой группы коров соответственно равна 0,6; 0,4 и 0,1. Определить вероятность того, что для взятой наудачу коровы жирность молока составит не менее 4%. Взятая наудачу корова дает молоко жирностью не менее 4%. Найти вероятность того, что эта корова из первой группы.
В первой урне 10 деталей, из них 8 стандартных. Во второй 6 деталей, из которых 5 стандартных. Из второй урны переложили в первую одну деталь. Какова вероятность того, что деталь, извлеченная после этого из первой урны, нестандартная?
Имеются две урны. В первой – семь красных шаров и три черных, во второй – три красных и четыре черных. Из первой урны переложили во вторую один шар, затем, перемешав шары, из второй урны переложили в первую один шар. Найти вероятность того, что шар, извлеченный после этого из первой урны, окажется красным.
Торговая фирма получает однотипные товары от трех поставщиков. Объемы поставок товаров относятся как 1 : 2 : 3. Известно, что удельный вес товаров высокого качества от первого поставщика составляет 2/3 , второго 3/4 и третьего 5/6 . Найти вероятность того, что взятая случайно единица товара будет высокого качества. Если взятая единица товара высокого качества, то наиболее вероятно, от какого поставщика она поступила?
Предприятие использует для производства продукта сырье трех других предприятий. Объем поступающего сырья относится в пропорции 1: 2: 5. Известно, что первое предприятие поставляет 60 % сырья высокого качества, второе 70 % и третье 90 %. Случайно взятая единица сырья оказалась высокого качества. Найти вероятность того, что она поступила от второго или третьего предприятия.
В первом ящике из 20 деталей 4 бракованных, во втором из 30 деталей 5 бракованных. Из первого во второй переложили две детали. Найти вероятность того, что деталь, извлеченная после этого из второго ящика, бракованная.
Исследование рынка хлебобулочных изделий показало, что на долю фирмы А приходится 40 % объема реализации продукции, фирмы В – 32 % и фирмы С – 28 %. Известно, что на долю хлеба приходится 65 % реализованной продукции фирмы А, 40 % - фирмы В и 70 % - фирмы С. Определить долю каждой фирмы на рынке хлеба.
Для посева заготовлены семена 4 сортов пшеницы, из которых 20% семян 1-го сорта, 30% - 2-го сорта, 10% - 3-го сорта и 40% - 4-го сорта. Вероятность того, что из зерна вырастет колос, содержащий не менее 40 зерен, для первого сорта равна 0,5, для второго – 0,3, для третьего – 0,2, для четвертого – 0,1. Найти вероятность того, что наудачу взятое зерно даст колос, содержащий не менее 40 зерен.
Из 25 студентов группы 5 студентов знают все 30 вопросов программы, 10 студентов выучили по 25 вопросов, 7 студентов по 20 вопросов, трое по 10 вопросов. Случайно вызванный студент ответил на два заданных вопроса. Какова вероятность, что он из тех трех студентов, которые подготовили по 10 вопросов?
Запасная деталь может находиться в одной из трех партий с вероятностями p1 = 0,2; p2 = 0,5; p3 = 0,3. Вероятности того, что деталь проработает положенное время без ремонта, равны соответственно 0,9; 0,8 и 0,7. Определить вероятность того, что: а) взятая наудачу деталь проработает положенное время; б) деталь, проработавшая положенное время, взята из второй или третьей партии.
Имеется 5 урн. В первой, второй и третьей находится по 4 белых и 6 черных шаров, в четвертой и пятой урнах по 2 белых и 3 черных шара. Случайно выбирается урна и из нее извлекается шар. Какова вероятность того, что была выбрана четвертая или пятая урна, если извлеченный шар оказался белым?
В первой бригаде производится в три раза больше продукции, чем во второй. Вероятность того, что производимая продукция окажется стандартной для первой бригады, равна 0,7, для второй – 0,8. Определить вероятность того, что взятая наугад единица продукции будет стандартной. Взятая наугад единица продукции оказалась стандартной. Какова вероятность, что она из второй бригады?
Покупатель с равной вероятностью посещает 3 магазина. Вероятность того, что он купит товар в первом магазине, равна 0,4, во втором - 0,3, в третьем - 0,2. Определить вероятность того, что покупатель купит товар. Пусть покупатель купил товар в одном из магазинов. Какова вероятность того, что он купил товар во втором или в третьем магазине?
3 ПОВТОРНЫЕ НЕЗАВИСИМЫЕ ИСПЫТАНИЯ
Схема испытаний Бернулли. Пусть опыт повторяется в неизменных условиях n раз. В каждом опыте некоторое событие А может наступить с вероятностью р и не наступить с вероятностью q = 1 – p. Вероятность того, что это событие наступит в n испытаниях ровно k раз вычисляется по формуле Бернулли:
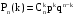 . (3.1) . (3.1)
Вероятности 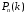 , где к = 0, 1, …, n, называются биноминальными вероятностями. , где к = 0, 1, …, n, называются биноминальными вероятностями.
При больших значениях n пользуются приближенными формулами.
Локальная формула Муавра – Лапласа. Если вероятность наступления некоторого события А в n независимых испытаниях постоянна, отлична от нуля и единицы, а число испытаний достаточно велико, причем npq ≥ 10, то вероятность 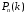 того, что в n испытаниях событие A наступит ровно k раз, приближенно равна (чем больше n, а р ближе к 0,5, тем точнее): того, что в n испытаниях событие A наступит ровно k раз, приближенно равна (чем больше n, а р ближе к 0,5, тем точнее):
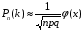 , где , где 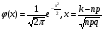 . (3.2) . (3.2)
Значение 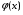 при заданном значении x находят по таблице (приложение 1), причем при заданном значении x находят по таблице (приложение 1), причем 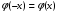 , а при x > 5, φ(x) = 0. , а при x > 5, φ(x) = 0.
Формула Пуассона. Точность приближенной формулы Муавра – Лапласа снижается по мере приближения вероятности р к нулю. В таких случаях пользуются приближенной формулой Пуассона. Если вероятность наступления каждого события в независимых испытаниях постоянна и мала, а число испытаний достаточно велико, причем npq < 10, то вероятность того, что в n независимых испытаниях событие наступит k раз находится по формуле:
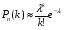 , (3.3) , (3.3)
где λ = nр.
Интегральная формула Муавра-Лапласа. При больших значениях n вероятность того, что число появления события будет находиться в некотором интервале от k1 до k2 раз, вычисляют по интегральной формуле Муавра-Лапласа. Если вероятность наступления события А в каждом из n независимых испытаний постоянна, отлична от нуля и единицы 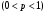 , а число испытаний достаточно велико, то вероятность того, что в n испытаниях событие произойдет от k1 до k2 раз, определяется по формуле: , а число испытаний достаточно велико, то вероятность того, что в n испытаниях событие произойдет от k1 до k2 раз, определяется по формуле:
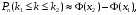 где где 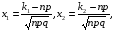 (3.4) (3.4)
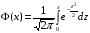 - функция Лапласа, - функция Лапласа, 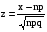 ; (3.5) ; (3.5)
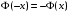 , при х > 5, Ф(х) = 0,5. , при х > 5, Ф(х) = 0,5.
Наивероятнейшее число появления события в независимых испытаниях. Наивероятнейшее число появления события А в повторных независимых испытаниях (kо) определяется из неравенств:
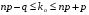 . (3.6) . (3.6)
Наивероятнейшее число kо – число целое. Если (np - q) – целое число, то имеется два наивероятнейших числа.
Вероятность того, что в независимых испытаниях абсолютное отклонение относительной частоты от постоянной вероятности не превзойдет некоторого числа 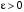 , определяется по формуле: , определяется по формуле:
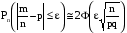 . (3.7) . (3.7)
Найти вероятность того, что при четырех подбрасываниях игральной кости 5 очков появится: а) два раза; б) хотя бы один раз; в) не менее 3 раз.
Всхожесть семян некоторого растения составляет 80 %. Найти вероятность того, что из пяти посеянных семян взойдут: а) пять семян; б) не менее четырех; в) не более одного.
Из 28 студентов группы 4 отличника. Наудачу вызываются три студента. Определить вероятности всех возможных значений числа отличников, которые могут оказаться среди вызванных трех студентов.
В семье 5 детей. Считая вероятности рождений мальчика и девочки одинаковыми, найти вероятность того, что среди этих детей: а) два мальчика; б) не более двух мальчиков; в) более двух мальчиков; г) не менее двух и не более трех мальчиков.
Вероятность того, что при сортировке изделий одно из них будет разбито, равна 0,005. Найти вероятность того, что из 200 изделий окажутся разбитыми: а) три изделия; б) не более двух; в) не менее двух изделий.
Станок автомат делает детали. Вероятность того, что деталь окажется бракованной, равна 0,01. Найти вероятность того, что среди 200 деталей окажется: а) четыре бракованных; б) не менее двух бракованных
Установлено, что вероятность обнаружения ошибки в каждом проверенном аудитором документе составляет 0,1. Определить вероятность того, что из 10 проверенных документов ошибка будет содержаться в одном. Вычислить по формулам Бернулли, Лапласа, Пуассона. Сравнить результаты, сделать выводы.
На факультете 900 студентов. Вероятность дня рождения каждого студента в данный день равна 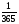 . Найти вероятность того, что найдутся три студента с одним и тем же днем рождения. . Найти вероятность того, что найдутся три студента с одним и тем же днем рождения.
Вероятность получения отличной оценки на экзамене равна 0,2. Найти наивероятнейшее число отличных оценок и вероятность этого числа, если сдают экзамен 100 студентов.
Вероятность того, что автомат при опускании одной монеты правильно сработает, равна 0,999. Найти наиболее вероятное число случаев неправильной работы автомата и вероятность этого числа случаев, если будет опущено 2000 монет.
Всхожесть клубней картофеля равна 80 %. Сколько нужно посадить клубней, чтобы наивероятнейшее число взошедших из них было равно 100?
Сколько раз нужно подбросить игральную кость, чтобы наивероятнейшее число выпадения 6 очков было равно 50?
Два равносильных противника играют в шахматы. Для каждого из них, что вероятнее выиграть: а) одну партию из двух или две из четырех; б) не менее двух партий из четырех или не менее трех партий из пяти. Ничьи во внимание не принимаются.
Бланк программированного опроса состоит из пяти вопросов. На каждый даны три ответа, среди которых один правильный. Какова вероятность, что методом угадывания студенту удастся выбрать по крайней мере четыре правильных ответа?
Вероятность того, что хотя бы одно изделие из 100 будет бракованным, составляет 0,1. Какой процент бракованных изделий выпускается предприятием.
При аудиторской проверке акционерного общества аудитор случайным способом отобрал 20 документов. Вероятность того, что документ имеет какую-то ошибку, равна 0,05. Определить вероятность того, что: а) только два документа будут содержать ошибку; б) хотя бы один документ будет содержать ошибку. Решить с помощью формул Бернулли и Пуассона и сравнить результаты.
Вероятность невыхода на работу из-за болезни равна 0,01 для каждого работника предприятия. Определить вероятность того, что в ближайший день не выйдет на работу хотя бы один из работников. Численность работников составляет 500 человек.
Вероятность успешной сдачи экзамена студентом составляет 0,8. Найти вероятность того, что из 100 студентов сдаст экзамен: а) 96 студентов; б) хотя бы 70 студентов; в) число сдавших экзамен составит от 70 до 90.
Известно, что 80 % специалистов в районе имеет высшее образование. Найти вероятность того, что из 100 наудачу отобранных человек высшее образование имеет: а) не менее 70; б) от 65 до 90 человек.
Вероятность заболевания гриппом в осенне-зимний период для населения поселка составляет 0,4. Найти вероятность того, что из 800 человек число заболевших составит: а) от 300 до 500 человек; б) более половины населения поселка.
Найти такое число k, чтобы с вероятностью 0,9 можно было утверждать, что среди 900 новорожденных более k мальчиков. Вероятность рождения мальчика 0,515.
В автопарке 70 машин. Вероятность поломки машины 0,2. Найти наиве-
роятнейшее число исправных автомобилей и вероятность этого числа.
Всхожесть хранящегося на складе зерна равна 80 %. Определить вероятность того, что среди 100 зерен: а) число всхожих составит от 68 до 90 шт.; б) доля (частость) всхожих зерен будет отличаться от вероятности 0,8 по абсолютной величине не более чем на 0,1?
Два стрелка одновременно производят выстрелы по мишени. Сколько нужно произвести залпов, если наивероятнейшее число залпов, при которых оба стрелка попадут в мишень, равно 8? Вероятность попадания в мишень при одном выстреле первого стрелка равна 0,5, а второго – 0,8.
Вероятность выигрыша по лотерейному билету составляет 0,1. Сколько нужно купить билетов, чтобы с вероятностью 0,99 выиграл хотя бы один из них?
Два стрелка производят по n выстрелов, причем каждый стреляет по своей мишени. Определить вероятность того, что у них будет по одинаковому числу попаданий, если вероятность попадания при каждом выстреле постоянна и равна 0,5.
В автопарке имеется 400 автомобилей. Вероятность безотказной работы каждого из них равна 0,9. С вероятностью 0,95 определить границы, в которых будет находиться доля безотказно работавших машин в определенный момент времени.
Всхожесть зерна 90 %. Определить вероятность того, что для отобранных случайным образом 100 зерен относительная частота всхожести будет отличаться от вероятности взойти p = 0,9 по абсолютной величине не более, чем на 0,1.
Вероятность что случайно взятый избиратель проголосует за данного кандидата, составляет 0,4. Найти вероятность того, что: а) из 100 опрошенных избирателей более половины проголосует за данного кандидата: в) доля избирателей, проголосовавших за данного кандидата, будет отклоняться от постоянной вероятности не более чем на 0,05?
Отдел контроля проверяет на стандартность 900 деталей. Вероятность того, что деталь стандартна, равна 0,9. С вероятностью 0,9544 найти границы, в которых будет заключено число стандартных деталей.
Известно, что 10 % делянок под овощами плохо обработано. Сколько нужно проверить делянок, чтобы с вероятностью 0,9973 можно было утверждать, что относительная частота засоренных делянок будет отличаться от вероятности засоренности по модулю не более чем на 0,01?
Для определения степени поражения винограда вредителями было обследовано 400 кустов. Вероятность поражения куста виноградника равна 0,03. Определить границы, в которых с вероятностью 0,9545 будет заключено число кустов, не пораженных вредителями.
По экспертной оценке, доля семей (р) с очень высокими доходами составляет 0,1. Каков должен быть объем выборки, чтобы с вероятностью не менее 0,99, погрешность в оценке доли семей с высокими доходами была не более 0,0025?
Страховая компания заключила 5000 договоров определенного вида. Вероятность страхового случая по каждому из них в течение года составляет 2 %. Найти: а) вероятность того, что в течение года страховых случаев будет не более 120: б) наивероятнейшее число страховых случаев; в) вероятность того, что абсолютная величина отклонения доли договоров со страховым случаем, будет отклоняться от постоянной вероятности не более чем на 0,5 %.
4 ДИСКРЕТНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Случайной величиной называется величина, которая в результате опыта может принять то или иное значение, причем до опыта заранее неизвестно, какое именно значение она примет. Случайные величины подразделяются на одномерные и многомерные.
Различают дискретные и непрерывные случайные величины. Дискретная случайная величина принимает отдельные, изолированные значения, а непрерывная величина принимает все значения на заданном промежутке.
Законом или таблицей распределения дискретной случайной величины называют упорядоченный перечень ее возможных значений и соответствующих им вероятностей.
Х
|
х1
|
х2
|
. . .
|
хn
|
, где 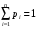 . .
|
рi
|
p1
|
p2
|
. . .
|
pn
| |
 Скачать 0.88 Mb.
Скачать 0.88 Mb.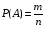 , (1.1)
, (1.1)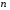 - общее число элементарных исходов (событий) в опыте или испытании;
- общее число элементарных исходов (событий) в опыте или испытании;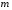 - число элементарных исходов (событий), благоприятствующих появлению события А.
- число элементарных исходов (событий), благоприятствующих появлению события А.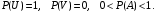 (1.2)
(1.2) 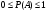 . (1.3)
. (1.3)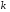 элементов из
элементов из 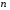 элементного множества по схеме без возвращений и с возвращениями:
элементного множества по схеме без возвращений и с возвращениями: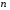 элементов по
элементов по 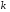 элементов без возвращений
элементов без возвращений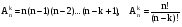 ; (1.4)
; (1.4)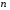 элементов
элементов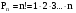 ; (1.5)
; (1.5)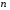 элементов по k элементовбез возвращений
элементов по k элементовбез возвращений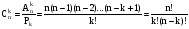 . (1.6)
. (1.6)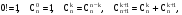
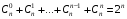 .
.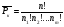 ; n1 + n2 + … + nm = n;
; n1 + n2 + … + nm = n; 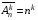 ;
; 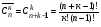 (1.7)
(1.7)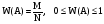 . (1.8)
. (1.8)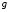 , брошенной в область
, брошенной в область 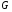 равна отношению меры (
равна отношению меры (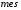 )области
)области 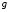 к мере области
к мере области 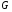 .
.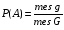 . (1.9)
. (1.9)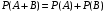 . (2.1)
. (2.1)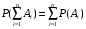 . (2.2)
. (2.2) или p + q = 1. (2.3)
или p + q = 1. (2.3)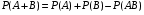 . (2.4)
. (2.4)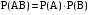 ;
; 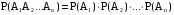 . (2.5)
. (2.5)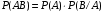 ; (2.6)
; (2.6) 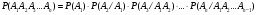 . (2.7)
. (2.7)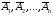 :
: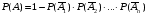 . (2.8)
. (2.8)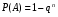 , где р + q = 1. (2.9)
, где р + q = 1. (2.9)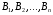 образующих полную группу событий. Будем называть события
образующих полную группу событий. Будем называть события 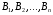 гипотезами для события А. Тогда вероятность наступления события А определяется по формуле:
гипотезами для события А. Тогда вероятность наступления события А определяется по формуле: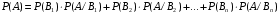 , (2.10)
, (2.10)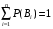 . (2.11)
. (2.11)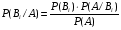 , (2.12)
, (2.12)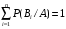 , (2.13)
, (2.13)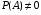 - находится по формуле полной вероятности.
- находится по формуле полной вероятности.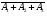 ; 4)
; 4) 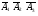 ; 5)
; 5)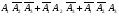 ; 6)
; 6) 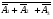 ;
; 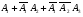 ; 8)
; 8) 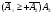 ; 9)
; 9) 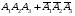 .
.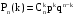 . (3.1)
. (3.1)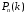 , где к = 0, 1, …, n, называются биноминальными вероятностями.
, где к = 0, 1, …, n, называются биноминальными вероятностями.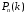 того, что в n испытаниях событие A наступит ровно k раз, приближенно равна (чем больше n, а р ближе к 0,5, тем точнее):
того, что в n испытаниях событие A наступит ровно k раз, приближенно равна (чем больше n, а р ближе к 0,5, тем точнее): 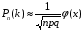 , где
, где 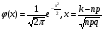 . (3.2)
. (3.2)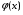 при заданном значении x находят по таблице (приложение 1), причем
при заданном значении x находят по таблице (приложение 1), причем 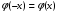 , а при x > 5, φ(x) = 0.
, а при x > 5, φ(x) = 0.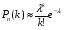 , (3.3)
, (3.3)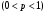 , а число испытаний достаточно велико, то вероятность того, что в n испытаниях событие произойдет от k1 до k2 раз, определяется по формуле:
, а число испытаний достаточно велико, то вероятность того, что в n испытаниях событие произойдет от k1 до k2 раз, определяется по формуле: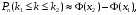 где
где 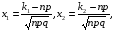 (3.4)
(3.4)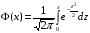 - функция Лапласа,
- функция Лапласа, 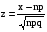 ; (3.5)
; (3.5)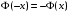 , при х > 5, Ф(х) = 0,5.
, при х > 5, Ф(х) = 0,5.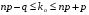 . (3.6)
. (3.6)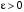 , определяется по формуле:
, определяется по формуле: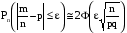 . (3.7)
. (3.7)
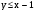 .
.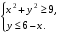
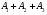 ; 2)
; 2) 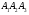 ;
;  – появление герба при
– появление герба при 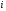 – ом подбрасывании
– ом подбрасывании 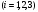 . Представить в виде сумм, произведений и сумм произведений событий Ai и
. Представить в виде сумм, произведений и сумм произведений событий Ai и 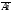 следующие события:
следующие события: 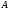 - появились все три герба;
- появились все три герба; 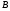 - появились все три цифры;
- появились все три цифры; 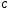 - появился хотя бы один герб;
- появился хотя бы один герб; 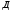 - появилась хотя бы одна цифра;
- появилась хотя бы одна цифра; 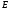 - появился только один герб;
- появился только один герб; 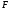 - появилась только одна цифра.
- появилась только одна цифра.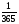 . Найти вероятность того, что найдутся три студента с одним и тем же днем рождения.
. Найти вероятность того, что найдутся три студента с одним и тем же днем рождения.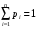 .
.