ТВ. и МС.( ЧТЮ) МЕТОДИЧКА 1,2 раздел. кубанский государственный аграрный университет
 Скачать 0.88 Mb. Скачать 0.88 Mb.
|
Таблица 8 - Распределение семей по величине месячного доходана одного члена семьи
С доверительной вероятностью 0,95 определить границы, в которых будет находиться средний месячный доход на одного члена семьи по району, а также доля семей с доходами менее 8,0 тыс. руб. на одного члена семьи. 11 В фирме проведен выборочный опрос 10% работников по вопросам изменения условий труда. Из 90 работников основного производства за изменение условий труда высказалось 65 человек, из 30 работников вспомогательного производства – 20, а из 25 работников, занятых управлением фирмой – 21. С доверительной вероятностью 0,95 определить границы, в которых будет находиться доля работников фирмы, поддерживающих изменение условий труда. 12 Для определения влияния микроэлементов на результаты откорма свиней проведен опыт на 8 группах животных. Рационы отличаются набором и дозами микроэлементов. Таблиц 9 - Результаты откорма свиней в опыте
С доверительной вероятностью 0,95 определить границы, в которых будет находиться среднесуточный прирост свиней по каждому рациону и по опыту в целом. 13 Проведен социологический опрос 500 избирателей по вопросам предстоящих выборов в региональные органы власти. Из опрошенных 22 % избирателей готовы поддержать кандидата А, а 36 % - кандидата Б. а) Определить 95 % доверительные интервалы для доли избирателей, которые отдадут свои голоса за кандидатов А и Б. б) Как изменится доверительный интервал для кандидата А, если предположить, что в выборах примут участие по первому варианту прогноза 30% избирателей, а по второму – 60%.
Статистической гипотезой называется всякое предположение о генеральной совокупности, проверяемое по выборке. Статистические гипотезы делятся на: параметрические – сформулированные относительно параметров (среднего значения, доли, дисперсии и др.) распределения известного вида; непараметрические – сформулированные относительно вида распределения (например, оценка по выборке нормальности генеральной совокупности). Выдвигаемая гипотеза называется основной или нулевой (Н0). Гипотеза, противоположная нулевой, называется конкурирующей или альтернативной (Н1). Так как проверка статистических гипотез осуществляется по выборочным данным, то возникает возможность принятия ошибочных решений. Различают ошибки первого и второго рода. Ошибка первого рода заключается в том, что будет отвергнута правильная гипотеза, т.е. когда в действительности верна Н0 гипотеза, а в результате проверки она была отвергнута и принята гипотеза Н1. Вероятность ошибки первого рода называется уровнем значимости и обозначается 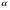 . . 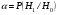 . (13.1) . (13.1)Ошибка второго рода состоит в том, что будет принята неправильная гипотеза, т.е. в действительности верна некоторая альтернативная гипотеза, а по выборочным данным была принята неверная гипотеза Н0. Вероятность ошибка второго рода обозначается 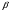 . .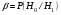 . (13.2) . (13.2)Существует правильное решение двух видов: 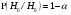 и и 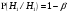 . (13.3) . (13.3)Статистическим критерием (К) называют случайную величину, с помощью которой при 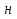 имают решение о принятии или отклонений нулевой гипотезы. имают решение о принятии или отклонений нулевой гипотезы.Проверка статистических гипотез обычно осуществляется в определенной последовательности. 1. Располагая выборочными данными, формулируют нулевую и конкурирующую гипотезы. 2. Задают уровень значимости 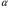 (обычно принимают (обычно принимают 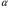 =0,1; 0,01; =0,1; 0,01; 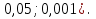 3. Выбирают критерий К, по которому будет проверяться выдвинутая гипотеза. Обычно используют следующие распределения критериев: u – нормальное распределение: 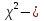 распределение Пирсона (xu – квадрат); распределение Пирсона (xu – квадрат); t – распределение Стьюдента; F – распределение Фишера - Снедекора. 4. На основании выборочных данных определяют фактически наблюдаемое значение критерия Кн. 5. В зависимости от вида альтернативной гипотезы находят, по соответствующей таблице, критические значения критерия для двусторонней 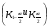 или односторонней области ( или односторонней области (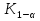 или или 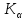 ). Если фактически наблюдаемые значения критерия попадают в критическую область, то нулевая гипотеза отвергается. В противном случае принимается нулевая гипотеза и считается, что она не противоречит выборочным данным (при этом существует возможность ошибки с вероятностью равной ). Если фактически наблюдаемые значения критерия попадают в критическую область, то нулевая гипотеза отвергается. В противном случае принимается нулевая гипотеза и считается, что она не противоречит выборочным данным (при этом существует возможность ошибки с вероятностью равной 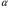 ). ).1 Имеется распределение сельскохозяйственных предприятий Краснодарского края по урожайности озимой пшеницы. Требуется проверить нулевую гипотезу, что совокупность предприятий по урожайности озимой пшеницы распределяется по нормальному закону. Уровень значимости принять равным 0,05. Таблица 10 – Распределение предприятий по урожайности озимой пшеницы
2 Выборочным методом изучались цены на картофель на продовольственных рынках города. Получено следующее распределение продавцов по уровню цен. Таблица 11 – Распределение продавцов по цене на картофель
При уровне значимости 0,05 проверить нулевую гипотезу, что цена на картофель на продовольственных рынках города распределяется по нормальному закону. 3 Сельскохозяйственные предприятия области по урожайности озимой пшеницы распределяются по нормальному закону с известным средним квадратическим отклонением 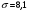 ц/га и генеральной средней урожайностью ц/га и генеральной средней урожайностью 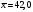 ц/га. Из генеральной совокупности извлечена выборка 50 хозяйств, по которой определена выборочная средняя урожайность ц/га. Из генеральной совокупности извлечена выборка 50 хозяйств, по которой определена выборочная средняя урожайность 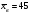 ц/га. ц/га.При уровне значимости 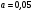 проверить нулевую гипотезу, что: проверить нулевую гипотезу, что:а) 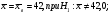 б) 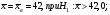 в) 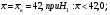 4 Производитель печенья утверждает, что вес одной пачки составляет 200 г. Выборочное взвешивание 10 пачек дало следующие результаты: 198; 197; 199; 200; 197; 201; 199; 195; 197; 200. При уровне значимости 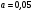 проверить гипотезу, что средний вес пачки печенья действительно составляет 200 г. проверить гипотезу, что средний вес пачки печенья действительно составляет 200 г. 5 Сливочное масло фасуется в пачки средним весом 170 г и средним квадратическим отклонением 3 г. Случайная выборка 20 пачек масла показала, что средний вес одной пачки равен 170,3 г. Проверить статистическую гипотезу при уровне значимости 0,05 о соответствии веса случайно взятой пачки масла, установленному весу. 6 Две фирмы производят однотипный товар. Утверждается, что 90% товаров первой фирмы реализуется повышенного качества, а второй фирмы 80 %. При выборочной проверке оказалось, что из 80 единиц товара первой фирмы повышенного качества 75, а из 60 единиц товара второй фирмы оказалось 45 единиц повышенного качества. При уровне значимости 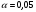 проверить гипотезы: а) о соответствии выборочных долей продукции высшего качества заявленной доле; б) о значимости различий в доле продукции высшего качества двух фирм. проверить гипотезы: а) о соответствии выборочных долей продукции высшего качества заявленной доле; б) о значимости различий в доле продукции высшего качества двух фирм.7 Провести две случайные выборки по одному из показателей приложения 4, объемами n1 и n2. Проверить нулевую гипотезу о равенстве выборочных средних значений, при уровне значимости 0,05 (предполагается, что дисперсии неизвестны и одинаковы): а) n1 = n2 =20; б) n1 = 20; n2 =15. 8 Проводилось испытание 8 сортов озимой пшеницы. Каждый сорт высевался на 6 делянках одинаковой площади. При 5% уровне значимости проверить гипотезу о существенности различий в средней урожайности двух сортов озимой пшеницы (номера сортов даются студенту преподавателем). Таблица 12 - Урожайность озимой пшеницы, ц/га
9 Произведено выборочное обследование 10% приусадебных участков восьми районов случайным бесповторным способом. Получены следующие результаты об урожайности овощей. Таблица 13 – Урожайность овощей в хозяйствах населения
При уровне значимости 0,05 по двум районам проверить гипотезы о равенстве: дисперсий, средних выборочных урожайностей, долей посевов овощей в площади приусадебных участков. 10 При уровне значимости 0,05 проверить гипотезу о равенстве успеваемости студентов по теории вероятностей и математике. Таблица 14 – Оценки студентов на экзаменах
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
