ТВ. и МС.( ЧТЮ) МЕТОДИЧКА 1,2 раздел. кубанский государственный аграрный университет
 Скачать 0.88 Mb. Скачать 0.88 Mb.
|
8 ЗАКОН БОЛЬШИХ ЧИСЕЛЗакон больших чисел представляет собой наиболее общий принцип, в результате которого количественные закономерности, присущие массовым случайным явлениям, отчетливо проявляются при достаточно большом числе наблюдений. Лемма Чебышева. Если все значения случайной величины Х неотрицательны, то вероятность того, что случайная величина Х будет не меньше некоторого числа t > 0 не больше, чем 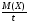 . .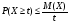 . (8.1) . (8.1)Неравенство Чебышева. Вероятность того, что абсолютное отклонение случайной величины Х от ее математического ожидания меньше некоторого числа ε > 0, не меньше чем 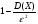 . .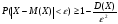 . (8.2) . (8.2)Теорема Чебышева. Если попарно – независимые случайные величины имеют конечные математические ожидания, дисперсии каждой из случайной величины не превосходят постоянного числа С, то среднее арифметическое этих величин сходится по вероятности к среднему арифметическому их математических ожиданий. Если 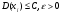 , то , то 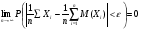 . (8.3) . (8.3)Воспользовавшись неравенством Чебышева, получаем 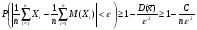 . (8.4) . (8.4)
Используя неравенство Чебышева, оценить вероятность того, что 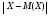 >3. >3.
Используя неравенство Чебышева, оценить вероятность того, что 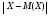 < 2,5. < 2,5.
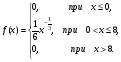 а) С помощью неравенства Чебышева оценить вероятность того, что 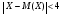 . б) Определить вероятность того, что . б) Определить вероятность того, что 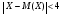 . .
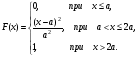 а) С помощью неравенства Чебышева оценить вероятность того, что 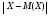 < < 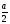 . б) Определить вероятность того, что . б) Определить вероятность того, что 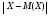 < < 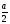 . .
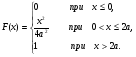 а) используя неравенство Чебышева, оценить вероятность того, что 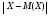 <а; б) определить вероятность того, что <а; б) определить вероятность того, что 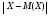 <а. <а.
Многомерной случайной величиной называют совокупность случайных величин, определенных на одном и том же пространстве элементарных событий. Она задается несколькими числами, рассматриваемыми совместно. Многомерные случайные величины могут быть дискретными, непрерывными и смешанными. Двумерная дискретная случайная величина (X, У) задается таблицей распределения, как совокупность пар значений (Х = хi, У = уj) и соответствующих им вероятностей 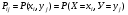 , , 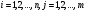 . .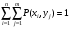 , , 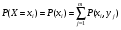 , , 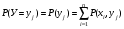 , ,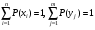 . (9.1) . (9.1)Условные вероятности 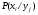 и и 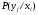 находятся по формулам: находятся по формулам: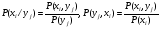 . (9.2) . (9.2)Многомерные случайные величины задаются функциями распределения. 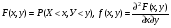 , (9.3) , (9.3)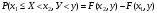 , , 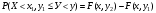 , ,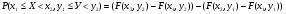 (9.4) (9.4)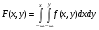 , (9.5) , (9.5)Для характеристики двумерной случайной величины используют математические ожидания, дисперсии и средние квадратические отклонения составляющих Х и У, а также корреляционный момент (ковариацию) cov(x,y) и коэффициент корреляции (r) 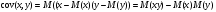 . (9.10) . (9.10)Для дискретных случайных величин Х, У: 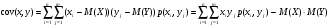 .(9.11) .(9.11)Для непрерывных случайных величин Х, У: 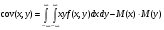 . (9.12) . (9.12)Коэффициент корреляции случайных величин Х и У: 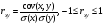 . (9.13) . (9.13)
а) б)
Определить: а) законы распределения составляющих случайных величин; б) математическое ожидание, дисперсию и среднее квадратическое отклонение составляющих Х и У; в) условный закон распределения случайной величины У, если Х = 2; г) условный закон распределения случайной величины Х, если У = 5.
а) б)
Определить: а) законы распределения составляющих; б) математическое ожидание, дисперсию и среднее квадратическое отклонение составляющих случайных величин Х и У;
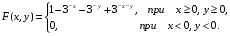 Определить: а) двумерную плотность вероятностей системы (Х, У); б) вероятность попадания случайной точки (Х, У) в прямоугольник, ограниченный прямыми х = 0, х = 2, у = 1, у = 3.
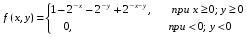
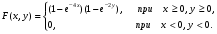 Найти двумерную плотность вероятности системы (Х, У).
Найти безусловные и условные законы распределения случайных величин урожайности (Х) и доз внесения удобрений (У), (а – число по указанию преподавателя).
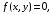 вне квадрата. вне квадрата.Определить: а) коэффициент а; б) М(Х), М(У); в) Д(Х), Д(У).
случайной величины 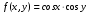 в квадрате в квадрате 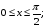 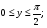 и и 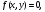 вне квадрата. Доказать, что составляющие Х и У независимы. вне квадрата. Доказать, что составляющие Х и У независимы.
случайной величины (Х,У): 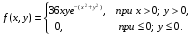 Найти математические ожидания и дисперсии составляющих.
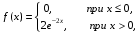 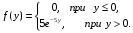 Найти: а) плотность совместного распределения системы; б) функцию распределения системы.
10. Цепи Маркова Результаты различных экспериментов или испытаний могут быть представлены в виде определенной последовательности букв или цифр, которые рассматриваются как процессы перехода от одного состояния в другое. Можно оценить вероятность такого перехода. Модель случайного процесса объединяет множество состояний и множество вероятностей перехода из одного состояния в другое. Множество (пространство) состояний может быть конечным и бесконечным. Последовательность состояний образует цепь Маркова, если в отдельном испытании система принимает одно из возможных состояний, не зависящее от результатов ранее произведенных испытаний. Вероятность 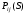 , есть условная вероятность перехода случайного процесса из состояния Si в состояние , есть условная вероятность перехода случайного процесса из состояния Si в состояние за один шаг. Так как она не зависит от номера испытания, то может обозначаться через за один шаг. Так как она не зависит от номера испытания, то может обозначаться через  . Первый индекс указывает номер предшествующего, а второй – последующего состояния. Если известны вероятности для любой пары состояния, то они могут быть представлены квадратной матрицей перехода. . Первый индекс указывает номер предшествующего, а второй – последующего состояния. Если известны вероятности для любой пары состояния, то они могут быть представлены квадратной матрицей перехода. 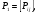 , где , где 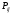 - элемент (вероятность), стоящий на пересечении i-ой строки и j-го столбца. - элемент (вероятность), стоящий на пересечении i-ой строки и j-го столбца.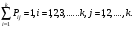 (10.1) (10.1)Вероятность перехода процесса из состояния S 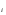 в состояние S в состояние S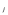 за n шагов обозначается за n шагов обозначается 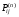 , а квадратная матрица всех этих вероятностей обозначается , а квадратная матрица всех этих вероятностей обозначается 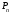 . Вероятность перехода процесса из состояния i в состояние j за два шага вычисляется по формуле полной вероятности. . Вероятность перехода процесса из состояния i в состояние j за два шага вычисляется по формуле полной вероятности. 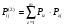 или в матричной записи или в матричной записи 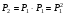 . (10.2) . (10.2)Аналогично получается матрица перехода за три шага 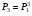 и за n – шагов и за n – шагов 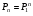 . (10.3) . (10.3)1 Вероятности перехода за один шаг в цепи Маркова задаются матрицей: а) 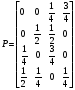 б) б) 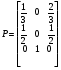 . .Найти число состояний системы. Построить граф, соответствующий матрице р. 2 Задана матрица вероятностей переходов 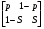 Каковы пределы изменений р и S? 3 В урне имеется 5 белых и черных шаров. Из урны случайно извлекается один шар, а обратно в урну возвращается один шар другого цвета. Опыт повто ряется неоднократно. Найти матрицу переходных вероятностей, состояниями которой является количество белых шаров в урне. Найти вероятности перехода за два шага. 4 Игральная кость перекладывается многократно с равной вероятностью случайным образом с одной грани на любую из соседних четырех граней, независимо от исхода предыдущего испытания. К какому пределу стремится при  вероятность того, что в момент времени t игральная кость лежит на грани «5», если в момент времени t=0, она находится в этом же положении? вероятность того, что в момент времени t игральная кость лежит на грани «5», если в момент времени t=0, она находится в этом же положении?5 Имеется пять стульев, расположенных один возле другого. Человек пересаживается с одного стула на рядом стоящий, причем эти перемещения определяются бросанием правильной игральной кости. Стулья обозначены буквами А,В,С,Д,Е. Вначале он сидит на среднем стуле С. Если человек сидит на крайнем стуле, то: возвращается на стул С, когда выпадет четное число очков; остается на том же месте при выпадении нечетного числа очков. Если он сидит не на крайнем стуле, то: перемещается налево при выпадении одного или двух очков; перемещается направо при выпадении трех или четырех очков; остается на том же месте при выпадении пяти или шести очков. Найти: а) матрицу вероятностей переходов за один шаг; б) вероятности следующих последовательностей: С,Д,Е,С,Д,А,С; С,В,Д,Е,Е,А; С,В,А,А,С,Д; С,Д,Е,С,Е,С; А,А,С,Д,Е,Е. 6 Студент, для получения профессионального образования, обучается в колледже в течение трех лет. Ежегодно он сдает комплексный экзамен. Если студент успешно сдаст экзамен, то он переводится на следующий курс или заканчивает колледж с дипломом специалиста. Если студент экзамен не сдает, то он остается на соответствующем курсе второй год. Вероятность успешной сдачи экзамена на первом году обучения составляет 0,7; втором – 0,8; третьем – 0,9. Указать подходящее число состояний системы. Найти матрицу вероятностей перехода за один шаг для ежегодных передвижений студента по курсам (первый, второй, третий год обучения, окончание колледжа). Определить вероятность, что студент будет обучаться на третьем курсе после сдачи второго экзамена. Определить среднее число лет, которые студент проводит в колледже. 11 ВАРИАЦИОННЫЕ РЯДЫ Ряд значений (вариант) признака, расположенных в порядке возрастания или убывания с соответствующими им весами (частотами или частостями), называется вариационными рядом (рядом распределения). Частота (ni) показывает, сколько раз встречается тот или иной вариант (значение признака) в статистической совокупности. Частость или относительная частота (wi) показывает, какая часть единиц совокупности принимает определенное значение или из интервала значений. В дискретных рядах перечисляются возможные значения признака  . Если признак непрерывный или число значений дискретного признака велико, то строят интервальный ряд распределения, в котором значения признака задаются в виде интервалов. При построении интервального ряда распределения число интервалов можно определить по формуле Стэрджесса: k=1+3,322 lg n, где n – число единиц совокупности. Величина интервала (h) определяется по формуле . Если признак непрерывный или число значений дискретного признака велико, то строят интервальный ряд распределения, в котором значения признака задаются в виде интервалов. При построении интервального ряда распределения число интервалов можно определить по формуле Стэрджесса: k=1+3,322 lg n, где n – число единиц совокупности. Величина интервала (h) определяется по формуле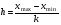 (8.1) (8.1)Дискретный ряд распределения можно изобразить графически в виде полигона распределения частот или частостей. В этом случае по оси абсцисс откладывают значения признака, а по оси ординат  соответствующие им частоты или частости. Полученные точки соединяются отрезками. соответствующие им частоты или частости. Полученные точки соединяются отрезками. Интервальные ряды изображают в виде гистограммы – фигуры, состоящей из прямоугольников. По оси абсцисс откладываются значения признака (границы интервалов), по оси ординат – частоты или частости. Дискретные и интервальные ряды можно графически представить в виде кумуляты или огивы. При построении кумуляты, в отличии от полигона, по оси ординат откладываются накопленные частоты или частости. При построении огивы на оси абсцисс наносятся точки, соответствующие накопленным частотам или частостям, а по оси ординат значения признака. Основной числовой характеристикой вариационного ряда является средняя арифметическая: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

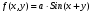 в квадрате
в квадрате 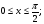
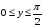 и
и