Статистика. Курс лекций по теории статистики
 Скачать 3.05 Mb. Скачать 3.05 Mb.
|
4.6. Статистические карты.Карты статистические представляют собой вид графических изображений статистических данных на схематичной географической карте, характеризующих уровень или степень распространения того или иного явления на определенной территории. Средствами изображения территориального размещения являются штриховка, фоновая раскраска или геометрические фигуры. Различают картограммы и картодиаграммы. Картограмма - это схематическая географическая карта, на которой штриховкой различной густоты, точками или окраской различной степени насыщенности показывается сравнительная интенсивность какого-либо показателя в пределах каждой единицы нанесенного на карту территориального деления (например, плотность населения по областям или республикам, распределение районов по урожайности зерновых культур и т.п.). Картограммы делятся на фоновые и точечные. Картограмма фоновая - вид картограммы, на которой штриховкой различной густоты или окраской различной степени насыщенности показывают интенсивность какого-либо показателя в пределах территориальной единицы. Картограмма точечная - вид картограммы, где уровень какого-либо явления изображается с помощью точек. Точка изображает одну единицу совокупности или некоторое их количество, чтобы показать на географической карте плотность или частоту появления определенного признака. Вторую большую группу статистических карт составляют картодиаграммы, представляющие собой сочетание диаграмм с географической картой. В качестве изобразительных знаков в картодиаграммах используются диаграммные фигуры (столбики, квадраты, круги, фигуры, полосы), которые размещаются на контуре географической карты. Картодиаграммы дают возможность географически отразить более сложные статистико-географические построения, чем картограммы. Глава 5. Средние показатели.5.1. Сущность средних показателейНаиболее распространенной формой статистических показателей, используемой в экономических исследованиях, является средняя величина, представляющая собой обобщенную количественную характеристику признака в статистической совокупности в конкретных условиях места и времени. Показатель в форме средней величины выражает типичные черты и дает обобщающую характеристику однотипных явлений по одному из варьирующих признаков. Он отражает уровень этого признака, отнесенный к единице совокупности. Широкое применение средних объясняется тем, что они имеют ряд положительных свойств, делающих их незаменимым инструментом анализа явлений и процессов в экономике. Важнейшее свойство средней величины заключается в том, что она отражает то общее, что присуще всем единицам исследуемой совокупности. Значения признака отдельных единиц совокупности колеблются в ту или иную сторону под влиянием множества факторов, среди которых могут быть как основные, так и случайные. Например, курс акций корпорации в целом определяется ее финансовым положением. В то же время, в отдельные дни и на отдельных биржах эти акции в силу сложившихся обстоятельств могут продаваться по более высокому или заниженному курсу. Сущность средней в том и заключается, что в ней взаимопогашаются отклонения значений признака отдельных единиц совокупности, обусловленные действием случайных факторов, и учитываются изменения, вызванные действием факторов основных. Это позволяет средней отражать типичный уровень признака и абстрагироваться от индивидуальных особенностей, присущих отдельным единицам. Типичность средней непосредственным образом связана с однородностью статистической совокупности. Средняя величина только тогда будет отражать типичный уровень признака, когда она рассчитана по качественно однородной совокупности. Так, если мы рассчитаем средний курс по акциям всех предприятий, реализуемых в данный день на данной бирже, то получим фиктивную среднюю. Это будет объясняться тем, что используемая для расчета совокупность является крайне неоднородной. В этом и подобных случаях метод средних используется в сочетании с методом группировок: если совокупность неоднородна - общие средние должны быть заменены или дополнены групповыми средними, т.е. средними, рассчитанными по качественно однородным группам. Категорию средней можно раскрыть через понятие ее определяющего свойства. Согласно этому понятию средняя, являясь обобщающей характеристикой всей совокупности, должна ориентироваться на определенную величину, связанную со всеми единицами этой совокупности. Эту величину можно представить в виде функции: f (х1, х2, ..., хn) (5.1.) Так как данная величина, в большинстве случаев, отражает реальную экономическую категорию, понятие определяющего свойства средней иногда заменяют понятием определяющего показателя. Если в приведенной выше функции все величины х1, х2, ..., хn заменить их средней величиной f (х1, х2, ..., хn)= Исходя из данного равенства и определяется средняя. На практике определить среднюю во многих случаях можно через исходное соотношение средней (ИСС) или ее логическую формулу: Так, например, для расчета средней заработной платы работников предприятия необходимо общий фонд заработной платы разделить на число работников: Числитель исходного соотношения средней представляет собой ее определяющий показатель. Для средней заработной платы таким определяющим показателем является фонд заработной платы. Независимо от того, какой первичной информацией мы располагаем - известен ли нам общий фонд заработной платы или заработная плата и численность работников, занятых на отдельных должностях, или какие-либо другие исходные данные - в любом случае среднюю заработную плату можно получить только через данное исходное соотношение средней. Для каждого показателя, используемого в экономическом анализе, можно составить только одно истинное исходное соотношение для расчета средней. Если, например, требуется рассчитать средний размер вклада в банке, то исходное соотношение будет следующим: Если же необходимо определить среднюю процентную ставку по кредитам, выданным на один и тот же срок, то потребуется следующее исходное соотношение: Однако от того, в каком виде представлены исходные данные для расчета средней, зависит, каким именно образом будет реализовано ее исходное соотношение. В каждом конкретном случае для реализации исходного соотношения потребуется одна из следующих форм средней величины: средняя арифметическая, средняя гармоническая, средняя геометрическая, средняя квадратическая, кубическая и т.д. Перечисленные средние объединяются в общей формуле средней степенной ( при различной величине k): 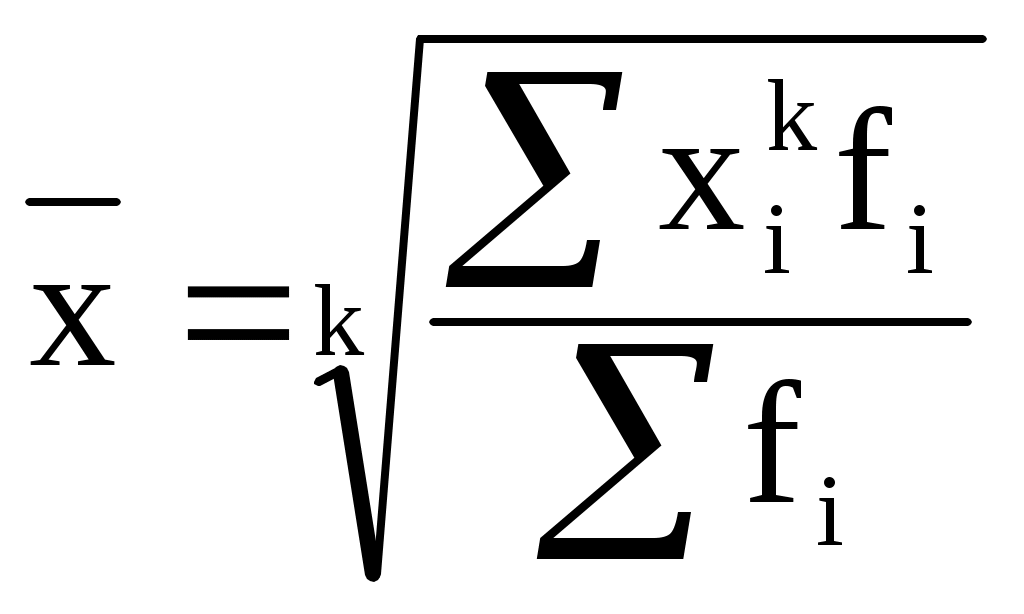 i= i=где х i - i-ый вариант осредняемого признака (i= f i - вес i-го варианта. Помимо степенных средних в экономической практике также используются средние структурные, среди которых наиболее распространены мода и медиана. При осреднении уровней динамических рядов применяются различные виды средней хронологической. 5.2. Средняя арифметическая и ее свойстваНаиболее распространенным видом средних величин является средняя арифметическая, которая, как и все средние, в зависимости от характера имеющихся данных может быть простой или взвешенной. Средняя арифметическая простая (невзвешенная). Эта форма средней используется в тех случаях, когда расчет осуществляется по несгруппированным данным. Предположим, пять торговых центров фирмы имеют следующий объем товарооборота за месяц:
Для того, чтобы определить средний месячный товарооборот в расчете на один центр, необходимо воспользоваться следующим исходным соотношением: Используя приведенные в предыдущем параграфе условные обозначения, запишем формулу данной средней: 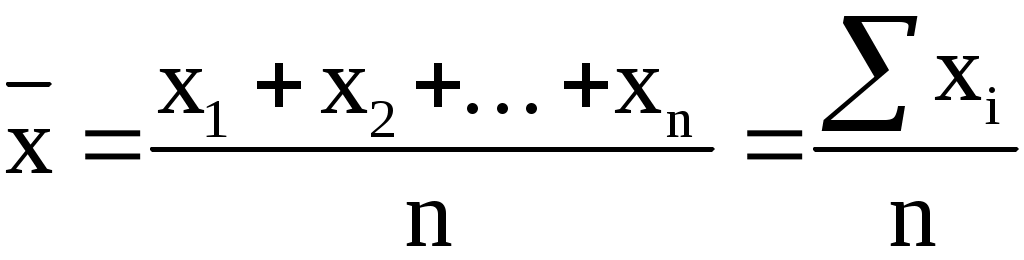 (5.3.) (5.3.)С учетом имеющихся данных получим: В данном случае мы использовали формулу средней арифметической простой (невзвешенной). Средняя арифметическая взвешенная. При расчете средних величин отдельные значения осредняемого признака могут повторяться, встречаться по несколько раз. В подобных случаях расчет средней производится по сгруппированным данным или вариационным рядам, которые могут быть дискретными или интервальными. Рассмотрим следующий пример: Таблица 5.1. Продажа акций АО “Дока-хлеб” на торгах фондовой секции ТМБ “Гермес” 11-17 мая 1994 г.
Определим по данному дискретному вариационному ряду средний курс продажи 1 акции, что можно сделать только используя следующее исходное соотношение: Чтобы получить общую сумму сделок необходимо по каждой сделке курс продажи умножить на количество проданных акций и полученные произведения сложить. В конечном итоге мы будем иметь следующий результат: Расчет среднего курса продажи произведен по формуле средней арифметической взвешенной: 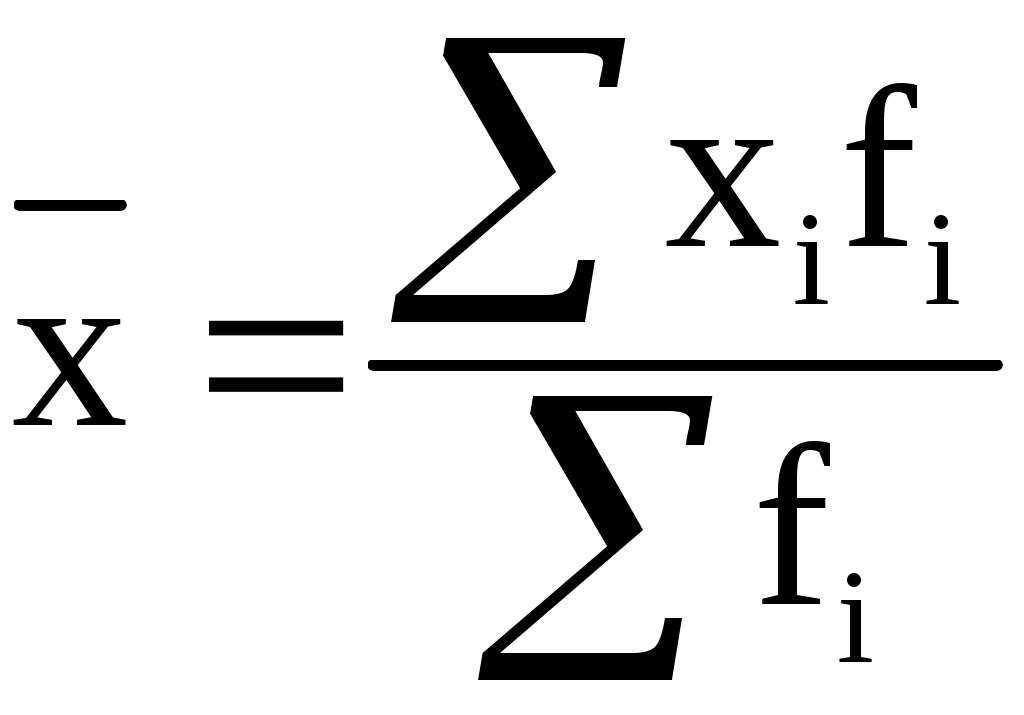 (5.4.) (5.4.)В отдельных случаях веса могут быть представлены не абсолютными величинами, а относительными ( в процентах или долях единицы). Так, в приведенном выше примере количество проданных в ходе каждой сделки акций соответственно составляет 26,3% (0,263); 15,8% (0,158) и 57,9% (0,579) от их общего числа. Тогда, с учетом несложного преобразования формулы (5.4.) получим: или На практике наиболее часто встречаемая при расчете средних ошибка заключается в игнорировании весов в тех случаях, когда эти веса в действительности необходимы. Предположим, имеются следующие данные: Таблица 5.2. Средние цены оптовых рынков на товар А
Можно ли по имеющимся данным определить среднюю цену данного товара по двум рынкам, вместе взятым? Можно, но только в том случае, когда объемы реализации этого товара на двух рынках совпадают. Тогда средняя цена реализации составит 42 руб. (доказательство этого правила будет приведено ниже.). Однако на первом рынке может быть реализовано, к примеру, 100 единиц товара, а на втором - 1000 единиц. Тогда для расчета средней цены потребуется уже средняя арифметическая взвешенная: Общий вывод заключается в следующем: использовать среднюю арифметическую невзвешенную можно только тогда, когда точно установлено отсутствие весов или их равенство. При расчете средней по интервальному вариационному ряду для выполнения необходимых вычислений от интервалов переходят к их серединам. Рассмотрим следующий пример: Таблица 5.3. Распределение менеджеров корпорации по возрасту
Для определения среднего возраста управленческого персонала найдем середины возрастных интервалов. При этом величины открытых интервалов (первого и последнего) условно приравниваются к величинам интервалов, примыкающих к ним (второго и предпоследнего). С учетом этого середины интервалов будут следующими: 22, 5 27,5 35,0 45,0 55,0 65,0 Используя среднюю арифметическую взвешенную, определим средний возраст менеджера данной корпорации: Свойства средней арифметической. Средняя арифметическая обладает некоторыми математическими свойствами, более полно раскрывающими ее сущность и в ряде случаев используемыми при ее расчете. Рассмотрим эти свойства: 1. Произведение средней на сумму частот равно сумме произведений отдельных вариантов на соответствующие им частоты: Действительно, если мы обратимся к приведенному выше примеру расчета среднего курса продажи акций (табл. 5.1.), то получим следующее равенство (за счет округления среднего курса правая и левая части равенства в данном случае будут незначительно отличаться): 1112,91900=1080500+1050300+11451100 2. Сумма отклонений индивидуальных значений признака от средней арифметической равна нулю: Для нашего примера: (1080-1112,9)500+(1050-1112,9)300+(1145-1112,9)1100=0 Математическое доказательство данного свойства сводится к следующему: 3. Сумма квадратов отклонений индивидуальных значений признака от средней арифметической меньше, чем сумма квадратов их отклонений от любой другой произвольной величины С: 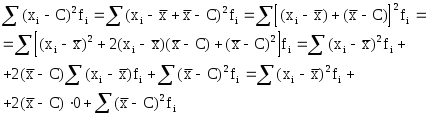 (5.8.) (5.8.)Следовательно, сумма квадратов отклонений индивидуальных значений признака от произвольной величины С больше суммы квадратов их отклонений от своей средней на величину На использовании этого свойства базируется расчет центральных моментов, представляющих собой характеристики вариационного ряда при где к определяет порядок момента (центральный момент второго порядка представляет собой дисперсию). 4. Если все осредняемые варианты уменьшить или увеличить на постоянное число А, то средняя арифметическая соответственно уменьшится или увеличится на ту же величину: Так, если все курсы продажи акций увеличить на 100 руб., то средний курс также увеличится на 100 руб.: 5. Если все варианты значений признака уменьшить или увеличить в А раз, то средняя также соответственно увеличится или уменьшится в А раз: 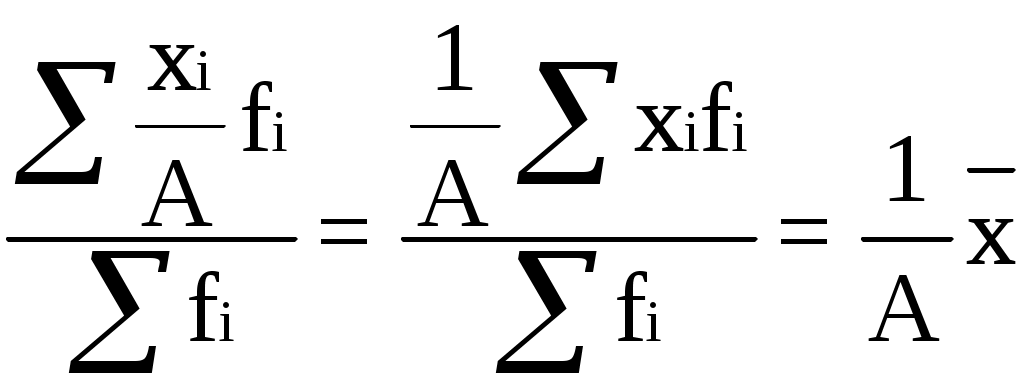 (5.10.) (5.10.)Предположим, курс продажи в каждом случае возрастет в 1,5 раза. Тогда и средний курс также увеличится на 50%: 6. Если все веса уменьшить или увеличить в А раз, то средняя арифметическая от этого не изменится: 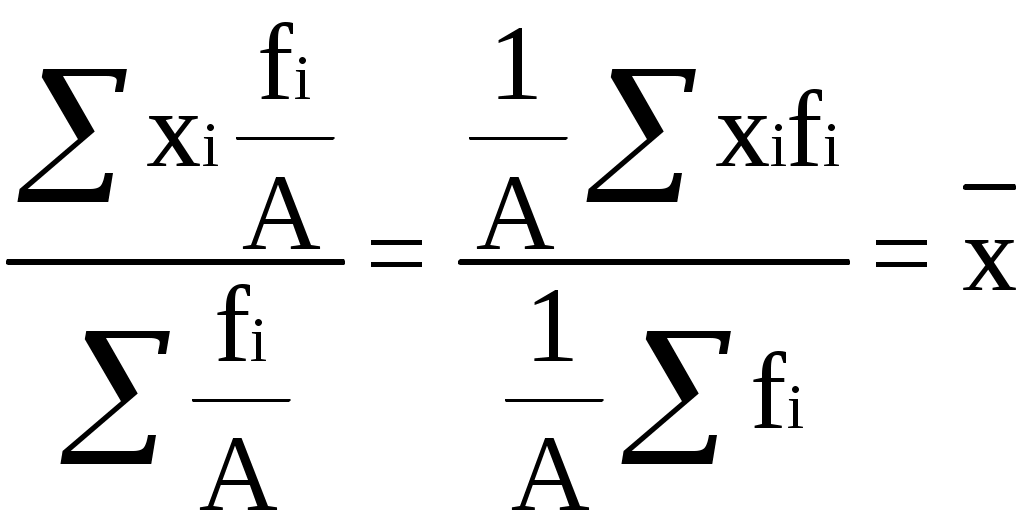 (5.11.) (5.11.)Так, в нашем примере удобнее было бы рассчитывать среднюю, предварительно поделив все веса на 100: Исходя из данного свойства, можно заключить, что если все веса равны между собой, то расчеты по средней арифметической взвешенной и средней арифметической простой приведут к одному и тому же результату. 5.3. Другие виды среднихПри расчете статистических показателей помимо средней арифметической могут использоваться и другие виды средних. Однако, в каждом конкретном случае, в зависимости от характера имеющихся данных, существует только одно истинное среднее значение показателя, являющееся следствием реализации его исходного соотношения. Средняя гармоническая взвешенная. Данная форма используется, когда известен числитель исходного соотношения средней, но неизвестен его знаменатель. Рассмотрим расчет средней урожайности, являющейся одним из основных показателей эффективности производства в агробизнесе: Таблица 5.4. Валовой сбор и урожайность подсолнечника по Центрально-Черноземному району (в хозяйствах всех категорий)
Средняя урожайность любой сельскохозяйственной культуры в среднем по нескольким территориям, агрофирмам, фермерским хозяйствам и т.п. может быть определена только на основе следующего исходного соотношения: Общий валовой сбор мы получим простым суммированием валового сбора по областям. Данные же о посевной площади отсутствуют, но их можно получить, разделив валовой сбор по каждой области на урожайность. С учетом этого определим искомую среднюю, предварительно переведя для сопоставимости тонны в центнеры: 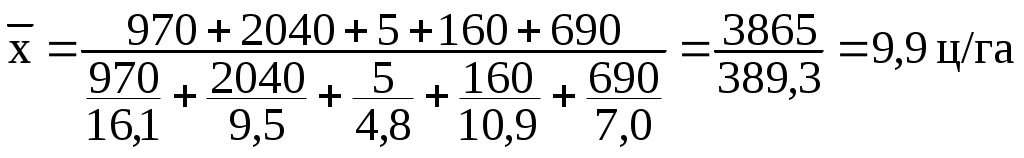 Таким образом, общая посевная площадь подсолнечника по Центрально-Черноземному району составляла 389,3 тыс.га, а средняя урожайность - 9,9 ц с одного гектара. В данном случае расчет произведен по формуле средней гармонической взвешенной: 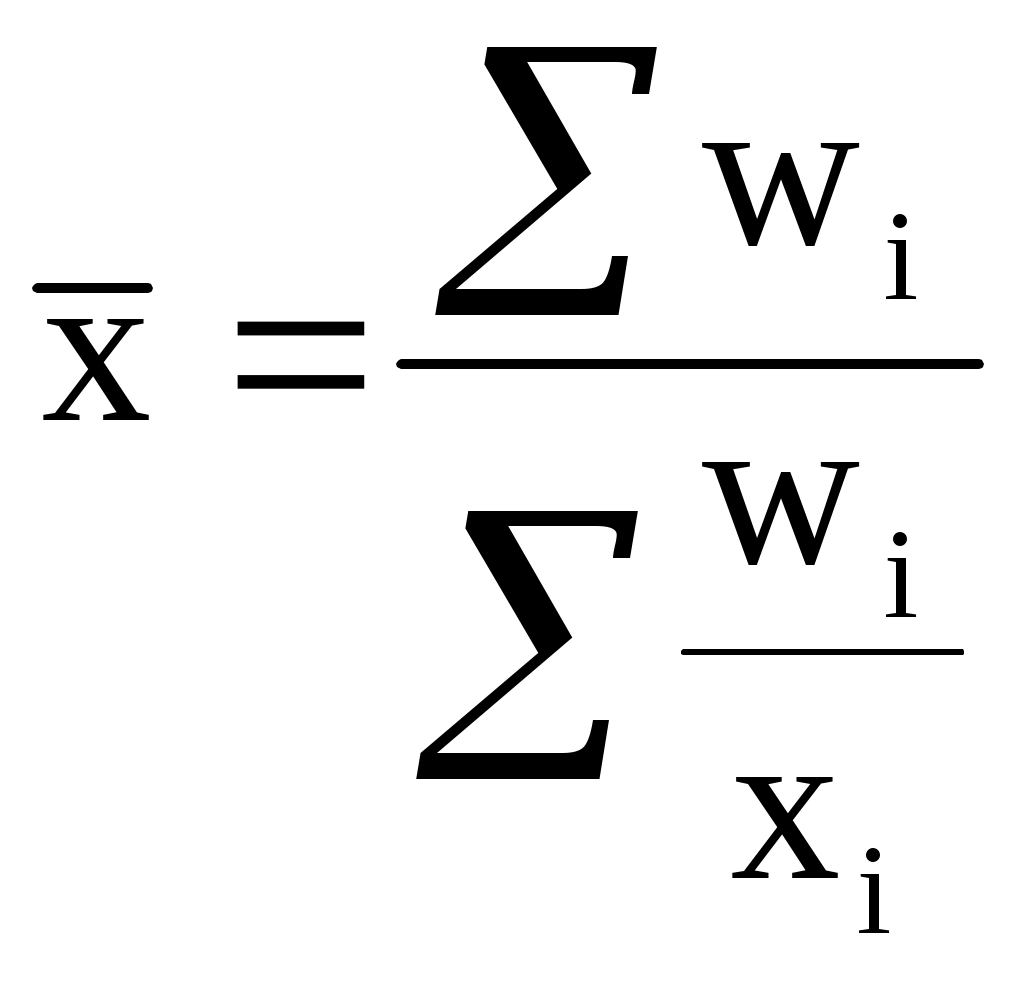 , где wi=xifi (5.12.) , где wi=xifi (5.12.)Данная формула используется для расчета средних показателей не только в статике, но и в динамике, когда известны индивидуальные значения признака и веса W за ряд временных интервалов. Средняя гармоническая невзвешенная. Эта форма средней, используемая значительно реже, имеет следующий вид: 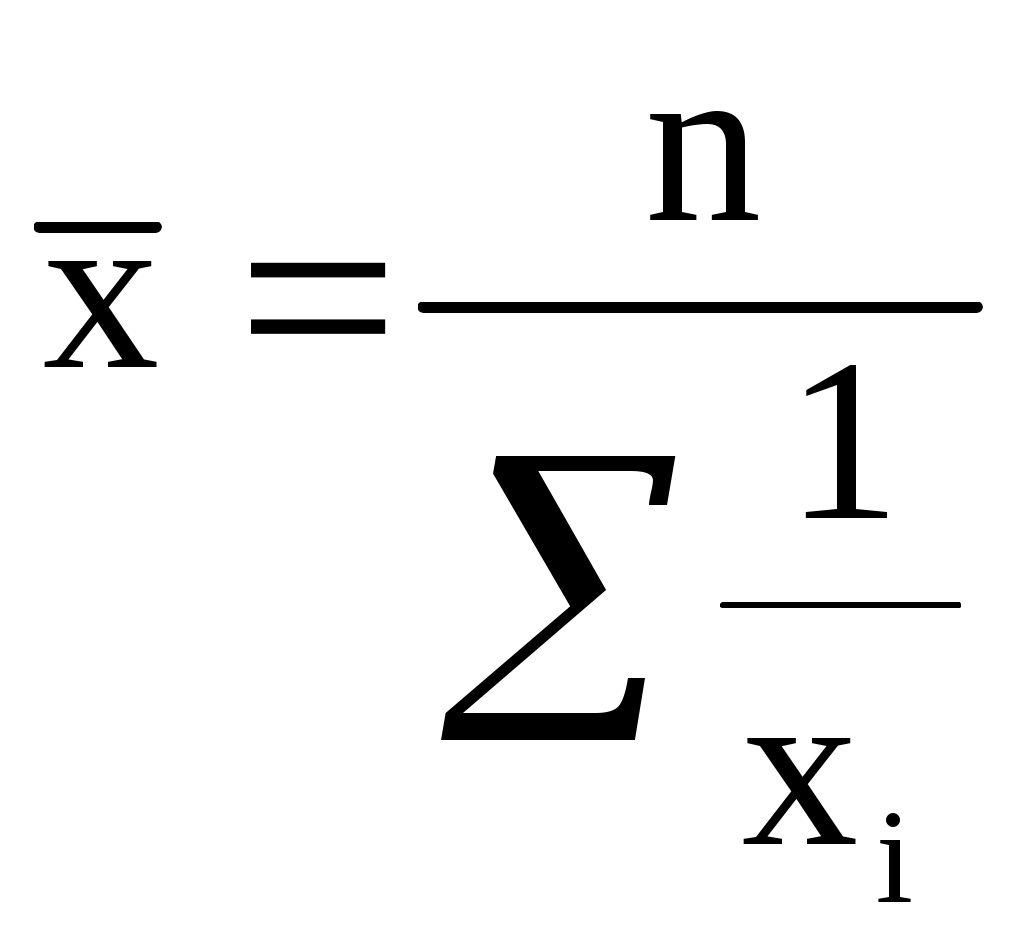 (5.13.) (5.13.)Для иллюстрации области ее применения воспользуемся упрощенным условным примером. Предположим, в фирме, специализирующейся на торговле по почте на основе предварительных заказов, упаковкой и отправкой товаров занимаются два работника. Первый из них на обработку одного заказа затрачивает 8 мин., второй - 14 мин. Каковы средние затраты времени на 1 заказ, если общая продолжительность рабочего времени у работников равна? На первый взгляд, ответ на этот вопрос заключается в осреднении индивидуальных значений затрат времени на 1 заказ, т.е. (8+14):2=11 мин. Проверим обоснованность такого подхода на примере одного часа работы. За этот час первый работник обрабатывает 7,5 заказов (60:8), второй - 4,3 заказа (60:14), что в сумме составляет 11,8 заказа. Если же заменить индивидуальные значения их предполагаемым средним значением, то общее число обработанных обоими работниками заказов в данном случае уменьшится: Подойдем к решению через исходное соотношение средней. Для определения средних затрат времени необходимо общие затраты времени за любой интервал (например, за час) разделить на общее число обработанных за этот интервал двумя работниками заказов: 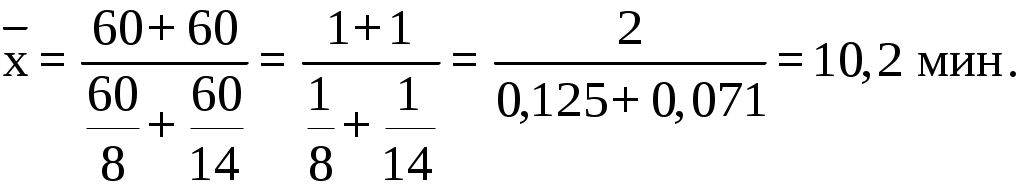 Если теперь мы заменим индивидуальные значения их средней величиной, то общее количество обработанных за час заказов не изменится: Подведем итог: средняя гармоническая невзвешенная может использоваться вместо взвешенной в тех случаях, когда значения wi для единиц совокупности равны (рабочий день у сотрудников одинаковый). Средняя геометрическая. Еще одной формулой, по которой может осуществляться расчет среднего показателя, является средняя геометрическая: (5.14.) Наиболее широкое применение этот вид средней получил в анализе динамики для определения среднего темпа роста, что будет рассмотрено в соответствующей главе. Средняя квадратическая. В основе вычислений ряда сводных расчетных показателей лежит средняя квадратическая: (5.15.) 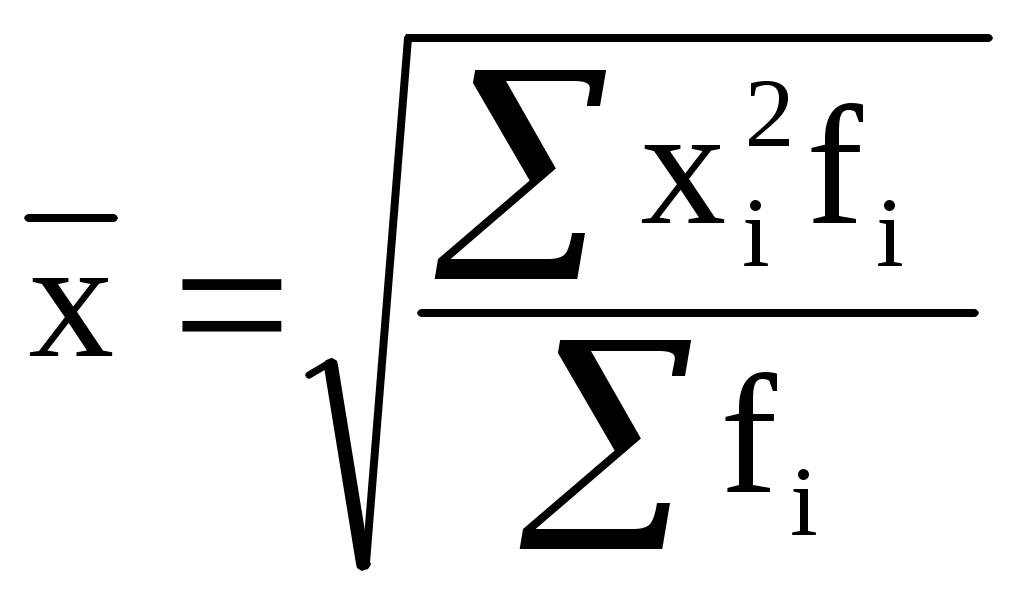 - взвешенная - взвешеннаяНаиболее широко этот вид средней используется при расчете показателей вариации. В статистическом анализе также применяются степенные средние 3‑го порядка и более высоких порядков. 5.4. Структурные средниеНаиболее часто используемыми в экономической практике структурными средними являются мода и медиана. Мода представляет собой значение изучаемого признака, повторяющееся с наибольшей частотой. Медианой называется значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности. Главное свойство медианы заключается в том, что сумма абсолютных отклонений значений признака от медианы меньше, чем от любой другой величины: Рассмотрим определение моды и медианы по несгруппированным данным. Предположим, что 9 торговых фирм города реализуют товар А по следующим оптовым ценам (тыс.руб.). 4,4 4,3 4,4 4,5 4,3 4,3 4,6 4,2 4,6 Так как чаще всего встречается цена 4,3 тыс.руб., то она и будет модальной. Для определения медианы необходимо провести ранжирование: 4,2 4,3 4,3 4,3 4,4 4,4 4,5 4,6 4,6 Центральной в этом ряду является цена 4,4 тыс.руб., следовательно, данная цена и будет медианой. Если ранжированный ряд включает четное число единиц, то медиана определяется как средняя из двух центральных значений. Если мода отражает типичный, наиболее распространенный вариант значения признака, то медиана практически выполняет функции средней для неоднородной, не подчиняющейся нормальном закону распределения совокупности. Она также используется в тех случаях, когда средняя не позволяет объективно оценить исследуемую совокупность вследствие сильного влияния максимальных и минимальных значений. Проиллюстрируем познавательное значение медианы следующим примером. Допустим, нам необходимо дать характеристику среднего дохода группы людей, насчитывающей 100 человек, из которых 99 имеют доходы в интервале от 100 до 1000 долл. в месяц, а месячные доходы последнего составляют 50000 долл.: № п/п 1 2 3 4 ... 50 51 ... 99 100 Доход 100 104 104 107 ... 162 164 ... 200 50000 (долл.) Если мы воспользуемся средней арифметической, то получим средний доход, равный примерно 600-700 долл., который не только в несколько раз меньше дохода 100-го человека, но и имеет мало общего с доходами остальной части группы. Медиана же, равная в данном случае 163 долл., позволит дать объективную характеристику уровня доходов 99% данной совокупности людей. Рассмотрим определение моды и медианы по сгруппированным данным (рядам распределения). Предположим, распределение торговых предприятий города по уровню розничных цен на товар А имеет следующий вид :
Определение моды по дискретному вариационному ряду не состав ляет большого труда - наибольшую частоту (60 предп.) имеет цена 55 руб., следовательно она и является модальной. Для определения медианного значения признака по следующей формуле находят номер медианной единицы ряда: где n - объем совокупности. В нашем случае Полученное дробное значение, всегда имеющее место при четном числе единиц в совокупности, указывает, что точная середина находится между 95 и 96 предприятиями. Необходимо определить, в какой группе находятся предприятия с этими порядковыми номерами. Это можно сделать, рассчитав накопленные частоты. Очевидно, что магазинов с этими номерами нет в первой группе, где всего лишь 12 торговых предприятий, нет их и во второй группе (12+48=60). 95-ое и 96-ое предприятия находятся в третьей группе (12+48+56=116) и, следовательно, медианой является цена 54 руб. В отличие от дискретных вариационных рядов определение моды и медианы по интервальным рядам требует проведения определенных расчетов на основе следующих формул : 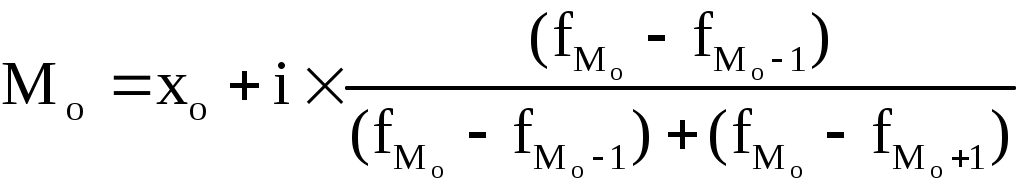 (5.17) (5.17)
и 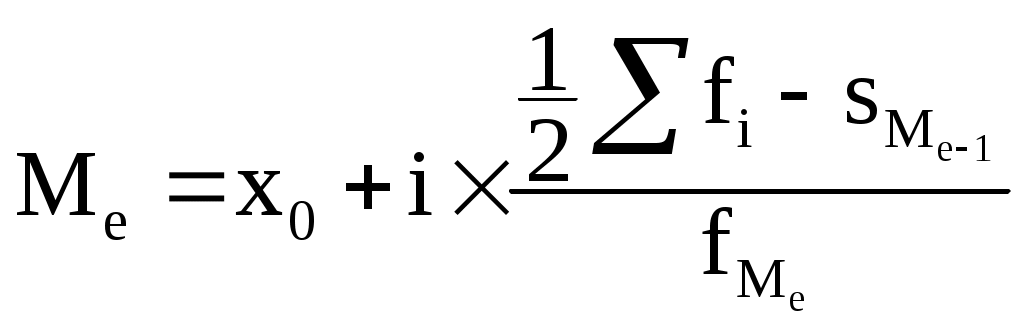 (5.18) (5.18)
Проиллюстрируем применение этих формул, используя данные таблицы 5.5. Информация, подобная представленной в этой таблице, необходима для получения четкого представления о покупательной способности населения страны или региона, для оценки эластичности спроса и, в конечном итоге, для выбора того или иного метода ценообразования и обоснования окончательной цены на товар. Таблица 5.5. Распределение населения РФ по уровню среднедушевого денежного дохода в январе-августе 1995 г.
Интервал с границами 200 - 300 в данном распределении будет модальным, так как он имеет наибольшую частоту. Использую формулу (5.17), определим моду : Для определения медианного интервала необходимо определять накопленную частоту каждого последующего интервала до тех пор, пока она не превысит 1/2 суммы накопленных частот (в нашем случае - 50%) :
Мы определили, что медианным является интервал с границами 300 - 400. Определим медиану : Соотношение моды, медианы и средней арифметической указывает на характер распределения признака в совокупности, позволяет оценить его асимметрию. Если Мо На основе полученных в последнем примере значений структурных средних можно заключить, что наиболее распространенным, типичным является среднедушевой доход порядка 260 тыс.руб. в месяц. В то же время, более половины населения располагает доходом свыше 370 тыс.руб. при среднем уровне 435 тыс.руб. (средняя арифметическая взвешенная). Из соотношения этих показателей следует вывод о правосторонней асимметрии распределения населения по уровню среднедушевых денежных доходов, что позволяет предполагать о достаточной емкости рынка дорогих товаров повышенного качества и товаров престижной группы. Глава 6. Анализ вариации.6.1. Основные показатели вариации.Информация о средних уровнях исследуемых показателей обычно бывает недостаточной для глубокого анализа изучаемого процесса или явления. Необходимо учитывать и разброс или вариацию значений отдельных единиц, которая является важной характеристикой изучаемой совокупности. В наибольшей степени вариации подвержены курсы акций, объемы спроса и предложения, процентные ставки в разные периоды и в разных местах. Основными показателями, характеризующими вариацию, являются размах, дисперсия, среднее квадратическое отклонение и коэффициент вариации. Для иллюстрации расчетов этих показателей воспользуемся следующими данными: Таблица 6.1 Итоги торгов на валютных биржах России 21 января 1999г. (спецсессия)
Простейшим показателем, уже использованным выше при группировке данных, является размах вариации. Он представляет собой разность максимального и минимального значений признака: R=Xmax-Xmin=22,83-22,40=0,43 руб. Недостатком данного показателя является то, что он оценивает только границы варьирования признака и не отражает его колеблемость внутри этих границ. Этого недостатка лишена дисперсия, рассчитываемая как средний квадрат отклонений значений признака от их средней величины:
По данным нашего примера определим средневзвешенный курс доллара по итогам всех торгов и рассчитаем дисперсию: Дисперсию в отдельных случаях удобнее рассчитывать по другой формуле, представляющей собой алгебраическое преобразование выражений (5.19.) и (5.20.):
Наиболее удобным и широко распространенным на практике показателем является среднее квадратическое отклонение. Оно определяется как квадратный корень из дисперсии и имеет ту же размеренность, что и изучаемый признак:
В нашем случае получим: Рассмотренная величина показывает, что курсы доллара на биржах отклонялись от средневзвешенного курса в среднем на 17,4 руб. Рассмотренные показатели позволяют получить абсолютное значение вариации, т.е. оценивают ее в единицах измерения исследуемого признака. В отличие от них, коэффициент вариации измеряет колеблемость в относительном выражении, относительно среднего уровня, что во многих случаях является предпочтительнее: Определим значение этого показателя по нашим данным: Рассчитанная величина свидетельствует об очень незначительном относительном уровне колеблемости курса доллара. Если V не превышает 33%, то совокупность по рассматриваемому признаку можно считать однородной. Информативность показателей вариации повышается, если они рассчитываются для целей сравнительного анализа. При этом показатели, рассчитанные по одной совокупности, сопоставляются с показателями, рассчитанными по другой аналогичной совокупности или по той же самой, но относящейся к другому периоду времени. Например, исследуется динамика вариации курса доллара по недельным или месячным данным. 6.2. Использование показателей вариации в анализе взаимосвязей.Показатели вариации могут быть использованы не только в анализе колеблемости или изменчивости изучаемого признака, но и для оценки степени воздействия одного признака на вариацию другого признака, т.е. в анализе взаимосвязей между показателями. При проведении такого анализа исходная совокупность должна представлять собой множество единиц, каждая из которых характеризуется двумя признаками - факторным и результативным. Факторным называется признак, оказывающий влияние на взаимосвязанный с ним признак. В свою очередь, этот второй признак, подверженный влиянию, называется результативным. Для выявления взаимосвязи исходная совокупность делится на две или более групп во факторному признаку. Выводы о степени взаимосвязи базируются на анализе вариации результативного признака. При этом применяется правило сложения дисперсий: где Межгрупповая дисперсия отражает ту часть вариации результативного признака, которая обусловлена воздействием признака факторного. Это воздействие проявляется в отклонении групповых средних от общей средней: 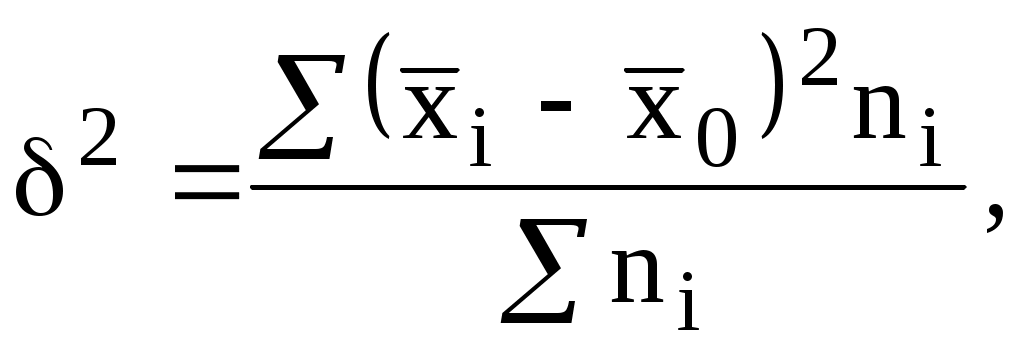 (6.9) (6.9)где Если факторный признак, по которому производилась группировка, не оказывает никакого влияния не признак результативный, то групповые средние будут равны между собой и совпадут с общей средней. В этом случае межгрупповая дисперсия будет равна нулю. Средняя из внутригрупповых дисперсий отражает ту часть вариации результативного признака, которая обусловлена действием всех прочих неучтенных факторов, кроме фактора, по которому осуществлялась группировка: где Теснота связи между факторным и результативным признаком оценивается на основе эмпирического корреляционного отношения: 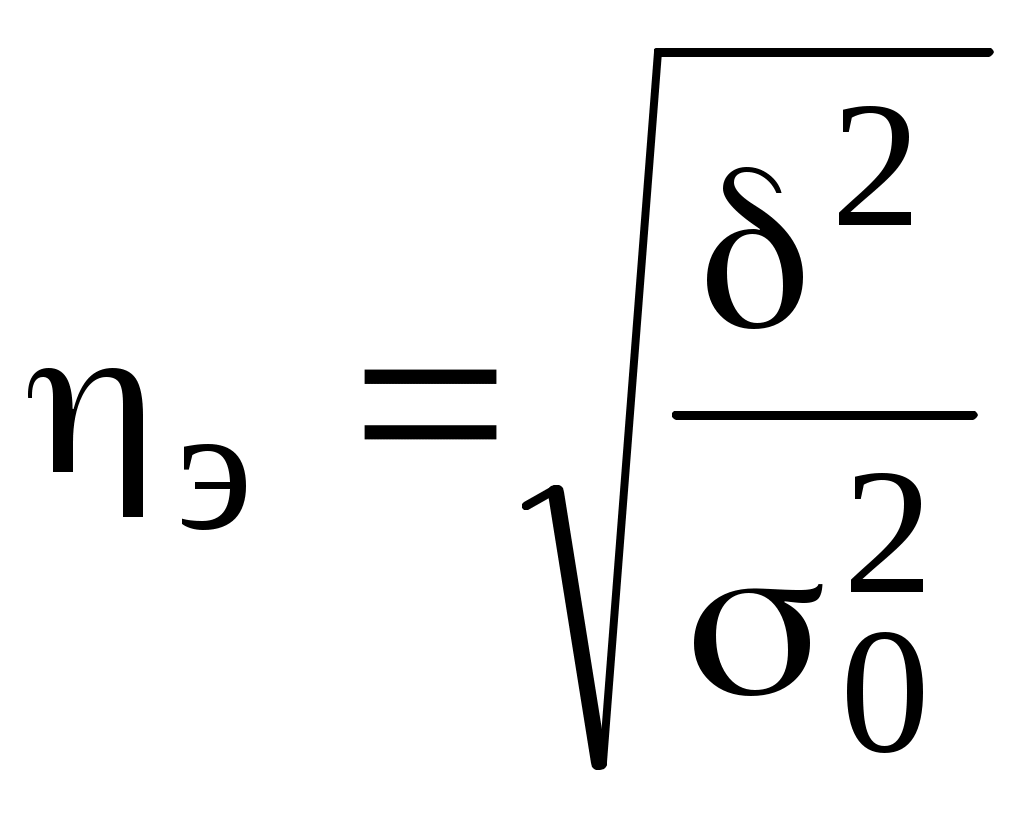 (6.11) (6.11)Данный показатель может принимать значения от 0 до 1. Чем ближе к 1 будет его величина, тем сильнее взаимосвязь между рассматриваемыми признаками. На следующем условном примере исследуем зависимость между собственными и привлеченными средствами коммерческих банков региона: Таблица №6.2
Если взаимосвязь между рассматриваемыми показателями существует, то она обусловлена влиянием объема собственных средств на объем привлеченных средств. Поэтому объем собственных средств выступает в данном примере в качестве факторного признака (X), а объем привлеченных средств в качестве результативного признака (Y). Произведем группировку банков, выделив две группы по величине собственных средств, например, группу “да 100 млн.руб.” и группу “100 млн. руб. и более”. Результаты такой группировки представлены в следующей таблице: Таблица №6.3
Расчет эмпирического корреляционного отношения включает несколько этапов: рассчитываем групповые средние: где i- номер группы; j- номер единицы в группе. 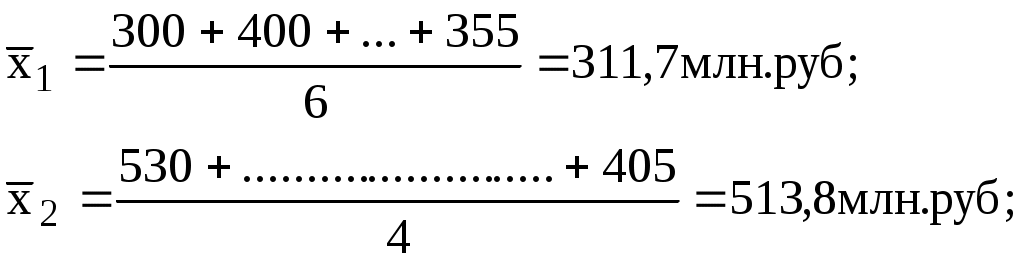 В данном примере при расчете групповых средних мы использовали невзвешенные формулы. Однако, при повторении вариантов для расчета необходимо использовать средние взвешенные. 2) рассчитываем общую среднюю: Данную среднюю также можно было получить как отношение суммы всех единиц исходной совокупности (без учета деления на группы) к объему всей совокупности, т.е. к общему числу единиц. 3) рассчитываем внутригрупповые дисперсии: 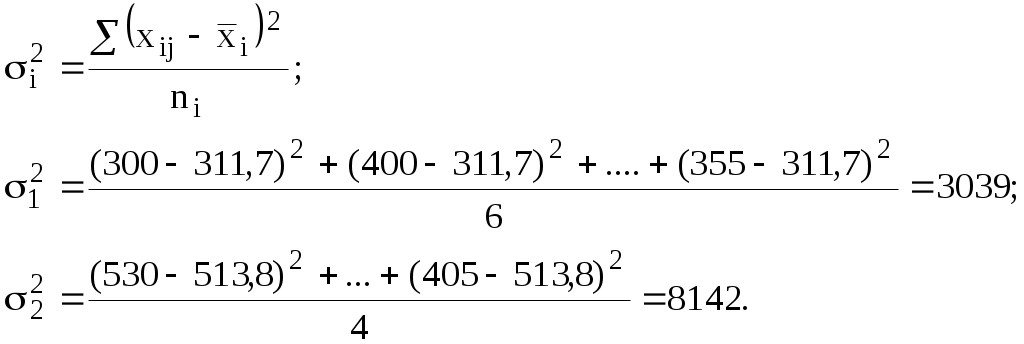 Если бы варианты имели веса, то для расчета внутригрупповых дисперсий также требовались бы взвешенные формулы. 4) вычисляем среднюю из внутригрупповых дисперсий: 5) определяем межгрупповую дисперсию: находим общую дисперсию по правилу сложения: На этом этапе возможна проверка правильности выполненных ранее расчетов. Если возвратиться к исходной совокупности и не раздета ее на группы рассчитать дисперсию признака “у”, то она должна совпасть с общей дисперсией, полученной по правилу сложения. рассчитываем эмпирическое корреляционное отношение: Полученная величина свидетельствует о том, что фактор, положенный в основание группировки (собственные средства), существенно влияет на размер привлеченных банками средств. |