маркетинглр. Маркетинг ЛР. Лабораторная работа Изучение и прогнозирование покупательского спроса, анализ реакции рынка
 Скачать 217.64 Kb. Скачать 217.64 Kb.
|
Лабораторная работа № 1.«Изучение и прогнозирование покупательского спроса, анализ реакции рынка»Цель данной лабораторной работы – научиться обрабатывать большой массив данных об изменениях основных факторов внешней среды за определенный период времени, т. е. провести маркетинговый анализ рынка, выявить закономерности развития фирмы и составить прогноз покупательского спроса на будущий период времени. Методические указания. Знание рынка и рыночных процессов становится повседневной заботой предпринимателей и руководителей предприятий. Основной проблемой анализа внешней среды является исследование закономерностей состояния и развития рынка, и, прежде всего, покупательского спроса. Разработка маркетинговой стратегии товарного производства и сбыта продукции остро нуждается в научно обоснованных предсказаниях перспектив развития рынка. При исследовании рынка в маркетинговом анализе выдвигаются три основные задачи: определение долговременных (стратегических) тенденций изменения покупательского спроса/товарооборота; выявление и моделирование влияния комплекса факторов на динамику спроса/товарооборота; прогнозирование спроса. Задание №1.В Приложении 1, по вариантам, приведены данные о товарообороте фирмы и о различных факторах (за два года по месяцам), которые оказывают влияние на покупательский спрос. Необходимо: проанализировать динамику товарооборота за рассматриваемый период времени; выявить наиболее существенные факторы изменения спроса и определить вид зависимости товарооборота от этих факторов; сделать анализ реакции рынка на изменения одного из факторов. Рекомендации для выполнения задания. Тенденции изменения спроса можно определять двумя методами: 1) графическое отображение динамики товарооборота за период времени и выявление общей тенденции, для чего можно использовать мастер диаграмм MS Excel; 2) аналитический расчет индексов изменения товарооборота. Выявление влияния факторов спроса можно провести построением факторных моделей или с помощью регрессионного анализа, инструмент которого предусмотрен в MS Excel. Существует ряд условий и ограничений применения корреляционно-регрессионных методов: исследуемая совокупность должна быть однородна, ее объем должен быть достаточно велик, вариация изучаемых признаков должна носить стохастический, вероятностный характер. Для выполнения данной лабораторной работы корреляционно-регрессионный анализ выполняется в следующей последовательности: 1) необходимо определить вид зависимости y=f(x), где y – товарооборот, x – фактор, влияющий на товарооборот, f(x) – искомая функция зависимости товарооборота от фактора (ов) внешней среды. Форма зависимости в соответствии с характером изменения результативного признака может быть линейной или нелинейной. 2) с помощью функции КОРРЕЛ() MS Excel находятся коэффициенты корреляции (rxy) между результирующим фактором (объемом товарооборота) и экзогенными факторами. Данный коэффициент позволяет выявить тесноту связи между анализируемыми признаками. Если rxy близок к нулю, то это свидетельствует об отсутствии тесной связи между X и Y, и наоборот, если rxy стремится к единице, то связь между X и Y довольно тесная. 3) далее подбирается регрессионная модель зависимости результирующего фактора от тех факторов, коэффициент корреляции с которыми близок к единице (по модулю). Для оценки адекватности построенной модели используются значения коэффициента детерминации: 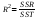 ; (1) ; (1)где SSR – сумма квадратов, обусловленных регрессией: 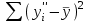 ; ;yi”- прогнозное значение товарооборота, рассчитанное по найденной зависимости; 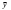 - среднее значение товарооборота за период времени n. - среднее значение товарооборота за период времени n.SST = SSR + SSE, где SSE – сумма квадратов ошибок: 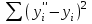 ; ;yi – фактическое значение товарооборота в период времени i. Если 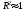 , то можно считать, что зависимость подобрана правильно. , то можно считать, что зависимость подобрана правильно.4) реакцию рынка на изменения факторов принято называть эластичностью. Теоретический коэффициент эластичности позволяет определить реакцию спроса для каждой точки регрессионной кривой: 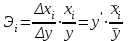 ; где Δ - знак прироста; ; где Δ - знак прироста; 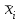 и и 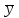 – среднемесячные значения цены и товарооборота соответственно; y' – первая производная функции (в линейном уравнении равна коэффициенту регрессии |a| при x). – среднемесячные значения цены и товарооборота соответственно; y' – первая производная функции (в линейном уравнении равна коэффициенту регрессии |a| при x).При Э<1 проявляется явление инфраэластичности, товар считается неэластичным, и спрос не поддается регулированию; при Э=1 спрос считается унитарным или слабоэластичным, его регулирование не имеет смысла; при Э>1 проявляется явление ультраэластичности, спрос поддается регулированию путем изменения цен или дохода. У приведенной формулы (ее называют эмпирическим коэффициентом эластичности), несмотря на ее простоту и доступность, имеется существенный недостаток: она отражает влияние на спрос одного фактора, при этом подразумевается, что изменение целиком обусловлено действием данного фактора, хотя на самом деле это не так. На спрос одновременно влияет комплекс факторов. По параметрам многофакторного уравнения регрессии можно построить «чистые» коэффициенты эластичности (их называют «теоретическими»), освобожденные от влияния других факторов. Пример. Необходимо найти зависимость товарооборота от ряда факторов, приведенных в таблице 1.1. Таблица 1.1. Исходные данные о факторах, влияющих на товарооборот
1) Определим вид зависимости, для этого построим диаграмму, приведенную на рисунке 1.1. Для наглядности определения вида зависимости добавим линию тренда. Если зависимость линейная, то уравнение y=f(x) примет вид: y = a1x1+a2x2+…anxn, где n – количество факторов, от которых зависит товарооборот. 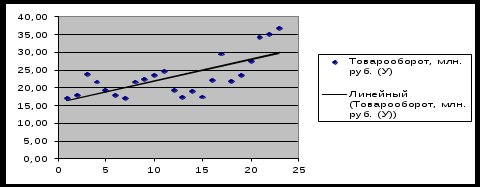 Рис. 1.1. Диаграмма товарооборота с линией тренда. 2) Вычислим значения корреляции для товарооборота с каждым из факторов (таблица 1.2): Таблица 1.2. Значения корелляции товарооборота с факторами.
Выберем те значения, которые наиболее близки к ±1. В рассматриваемом случае это будут численность населения и цена реализации. 3) при помощи пакета анализа построим вид зависимости выделенных факторов: для подключения пакета анализа необходимо выбрать в меню Сервис -> Надстройки -> Пакет анализа. После этого в меню Сервис -> Анализ данных -> Регрессия выберите диапазоны входных переменных для у – товарооборот, для х – численность населения и цена реализации. В результате будут получены следующие данные, приведенные в таблице 1.3. Таблица 1.3. Результат работы пакета анализа – регрессия. ВЫВОД ИТОГОВ
Таким образом, уравнение y=f(x) примет вид y=11,4x1 - 0,1x2 + 35. Значение R2=0,9037616. Это значение достаточно близко к 1, следовательно, построенная модель адекватна. 4) Теоретическая эластичность Э1=0,029023704; Э2= 0,43851129 – полученные значения меньше 1, товарооборот не зависит от численности населения и цены реализации. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
