Курс лекции по ЭУТТ.. Вахламов. Лекции по дисциплине Энергетические установки транспортной техники для бакалавров высших учебных заведений, обучающихся по специальности

• Название: Лекции по дисциплине Энергетические установки транспортной техники для бакалавров высших учебных заведений, обучающихся по специальности
• Анкор: Курс лекции по ЭУТТ.. Вахламов.doc
• Дата: 03.02.2017
• Размер: 5.99 Mb.
• Имя файла: Курс лекции по ЭУТТ.. Вахламов.doc
• Тип: Лекции; #2019
• страница: 11 из 20

Рис. 7.7. Наддув с механическим приводом Рис. 7.8. Турбонаддув:

1 - компрессор; 2 — турбина

Применение наддува в двигателях с искровым зажиганием осложняется возникновением детонационного сгорания и более вы­сокой тепловой напряженностью лопаток турбины.

Анализируя уравнение 7.1., можно определить и другие спо­собы увеличения мощности двигателя:

• увеличение рабочего объема V_hдвигателя является наиболее
простым способом повышения мощности. При этом происходит практически пропорциональное изменение массы заряда поступающего в цилиндры, что соответственно влияет на увеличению эффективной мощности.

Рабочий объем может быть увеличен как путем увеличена габаритных размеров цилиндров, так и повышением их числа несмотря на то, что увеличение габаритных размеров имеет свои преимущества, этот способ имеет такой существенный недостаток, как пропорциональный рост массы шатунно-поршневой группы, что увеличивает силы инерции деталей и снижает максимальную частоту вращения коленчатого вала;

• 
  увеличение плотности воздуха р можно получить с помощью
  наддува;
  
• 
  рост коэффициента наполнения может быть обеспечен путем создания более совершенных конструкций впускных трубопроводов и увеличения числа впускных клапанов, а также переводом бензиновых двигателей с карбюраторной системы питания к системе впрыска;
  
• 
  конструктивное совершенствование двигателей для увеличения η_м. Так, используя новые материалы, можно снизить механические потери на трение, а совершенствование газораспределительного и других механизмов обеспечивает снижение насосных потерь и потерь на привод вспомогательных узлов.
  

• 
  повышение индикаторного КПД η_і которое зависит от
  личных факторов, рассматривалось в подразделе 4.2.3;
  
• 
  согласно формуле (7.1) увеличение частоты вращения коленчатого вала п должно привести к пропорциональному росту N_е. Однако увеличение быстроходности вызывает рост газодинамического сопротивления при впуске свежего заряда, в результате чего понижается коэффициент наполнения. Кроме этого возрастают механические потери, тепловая и механичекая напряженность деталей. Поэтому повышение быстроходности двигателя должно сопровождаться соответствующий конструктивными решениями, снижающими отрицательные последствия увеличения значений п;
  

• использование обедненных горючих смесей приводит к плохой их воспламеняемости от электрического разряда, а применение электрофакельного зажигания существенно усложняет конструкцию двигателя, в частности газораспределительного механизма.

Эффективным способом увеличения мощности двигателя является улучшение смесеобразования, особенно в дизелях. Перспективным в этом направлении остаются создание топливной аппаратуры обеспечивающей высокое качество распыления, и интенсификаю турбулизации заряда в цилиндрах двигателя и камере сгорания, дробнее способы смесеобразования описаны в главе 8.
Контрольные вопросы
1. Как и почему изменяются основные параметры по нагрузочной характеристике дизеля?

2. Как и почему изменяются основные параметры по нагрузочной характеристике двигателя с искровым зажиганием?

3. Как и почему изменяются основные параметры двигателя по скоростной характеристике?

4. Как и почему изменяются основные параметры двигателя по регулировочной характеристике от состава смеси?

5. Как и почему изменяются основные параметры двигателя по регулировочной характеристике от угла опережения впрыскивания дизеля?

6. Как и почему изменяются основные параметры двигателя по регулировочной характеристике от угла опережения зажигания?

7. Как снимается нагрузочная характеристика?

8. Как снимается регулировочная характеристика двигателя с искровым зажиганием по составу смеси?

9. Как снимается регулировочная характеристика по углу опережения зажигания?

10. Как снимается скоростная характеристика?

11. Для чего необходима внешняя скоростная характеристика?

12. Сформулируйте назначение регуляторной характеристики.

13. Перечислите способы повышения мощности двигателя.

14. Напишите в развернутом виде формулу эффективной мощности.


Лекция 8: КИНЕМАТИКА И ДИНАМИКА ШАТУННО-КРИВОШИПНОГО МЕХАНИЗМА ПОРШНЕВОГО ДВИГАТЕЛЯ.

1. Кинематические характеристики движения.

2. Динамика кривошипно-шатунного механизма

3. Влияние конструктивных соотношений кривошипно-шатунного механизма на параметры двигателя
1. Кинематические характеристики движения.

В автомобильных двигателях в основном используются следую­щие типы кривошипно-шатунного механизма (рис. 8.1): централь­ный (аксиальный), смещенный (дезаксиальный). Комбинируя дан­ные схемы, можно сформировать кривошипно-шатунный меха­низм (КШМ) как линейного, так и многорядного многоцилинд­рового двигателя. При этом смещенный механизм возможен в двух вариантах. В первом случае ось цилиндра смещена относительно оси коленчатого вала, а во втором — ось поршневого пальца сме­щена относительно оси цилиндра.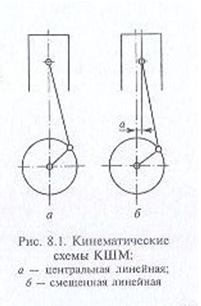



Рис. 8.1 Кинематические схемы КШМ:

а – центральная линия; б – смещенная линия
При работе двигателя основные элементы КШМ совершают различные виды перемещений. Поршень движется возвратно-по­ступательно. Шатун совершает сложное плоскопараллельное дви­жение в плоскости его качания. Кривошип коленчатого вала со­вершает вращательное движение относительно его оси.

Расчетная кинематическая схема КШМ представлена на рис. 8.2. Основными геометрическими параметрами, определяющими за­коны движения элементов центрального КШМ, являются: r — радиус кривошипа коленчатого вала; l_ш — длина шатуна.

Параметр λ = r/l_ш является критерием кинематического подо­бия центрального механизма. При этом для КШМ различных раз­меров, но с одинаковыми λ законы движения аналогичных эле­ментов подобны. В автотракторных ДВС применяют КШМ с λ = 0,24...0,31.

В смещенных КШМ имеется еще один геометрический пара­метр, влияющий на его кинематику, — смещение оси цилиндра (пальца) относительно оси коленчатого вала а. При этом относи­тельное смещение k = а/r является дополнительным к λ критери­ем кинематического подобия смещенных КШМ. Таким образом, подобные смещенные КШМ имеют одинаковые λ и k, где k изме­няется от 0,02 до 0,1.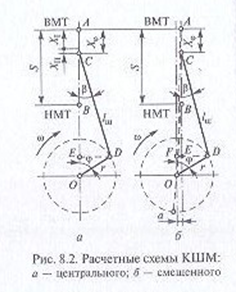


Рис. 8.2 Расчетные схемы КШМ: а – центральная; б – смещенная.
При кинематическом анализе КШМ приняты следующие до­пущения:

угловая скорость (частота вращения) коленчатого вала ω по­стоянна;

элементы КШМ абсолютно жесткие;

зазоры в подвижных сочленениях КШМ отсутствуют.

Кинематику КШМ можно полностью описать, если известны законы изменения во времени следующих параметров:

перемещения поршня X. Начало отсчета (X = 0) соответствует положению поршня в ВМТ; положительное направление отсчета принято при его движении от ВМТ к НМТ при вращении криво­шипа по ходу часовой стрелки;

угла поворота кривошипа φ (начало отсчета — положение кри­вошипа при нахождении поршня в ВМТ);

угла отклонения шатуна β от оси цилиндра (β = 0 при φ = 0).

Кинематика кривошипа. Вращательное движение кривошипа коленчатого вала определено, если известны зависимости угла по­ворота φ, угловой скорости ω и ускорения ε от времени t.

Для постоянной частоты вращения коленчатого вала φ = ωt и ω = πn/30.

Кинематика поршня. Кинематика возвратно-поступательно дви­жущегося поршня описывается зависимостями его перемещения Х_φ, скорости υ_φ и ускорения j_φ в функции угла поворота кривоши­па φ.

Перемещение поршня при повороте кривошипа на угол φ опре­деляется как сумма его смещений от поворота кривошипа на угол φ(X_I) и отклонения шатуна на угол β(Х_II): X = r + l_ш - r cosφ - l_ш соs β

или окончательно с учетом λ = r/l_ш X = r[(1-соsφ) + (1/λ)(1-соsβ)].

С достаточной для практических расчетов точностью можно упростить эту зависимость: X = r[(1 - соsφ) + (λ/4)(1 - соs2φ)] = Х_I+Х_II.

Скорость поршня определяется как первая производная от пе­ремещения поршня по времени:

и приближенно .

Максимального значения скорость достигает при φ + β = 90°, когда ось шатуна перпендикулярна радиусу кривошипа.

Для современных двигателей λ составляет 1,62... 1,64.

Ускорение поршня определяется производной от скорости пор­шня по времени:

и приближенно

В современных двигателях j = 5000... 20000 м/с².

Для дезаксиального КШМ приближенные значения υ и j име­ют вид:



С учетом того, что для современных двигателей произведение kλ = 0,01...0,05 и его влияние на кинематику механизма невели­ко, на практике им обычно пренебрегают.

Кинематика шатуна. Сложное плоскопараллельное движение шатуна складывается из движения его верхней головки с кинема­тическими параметрами поршня и его нижней кривошипной го­ловки с параметрами конца кривошипа. Кроме того, шатун со­вершает вращательное (колебательное) движение относительно точки сочленения с поршнем.

2. Динамика кривошипно-шатунного механизма

При работе двигателя в КШМ действуют следующие основные силовые факторы: силы давления газов, силы инерции движу­щихся масс механизма, силы трения и момент полезного сопро­тивления. При динамическом анализе КШМ силами трения обычно пренебрегают.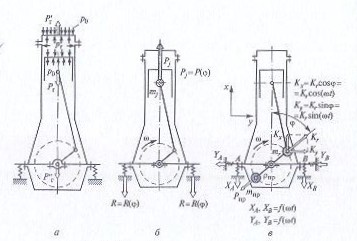



Рис. 8.3. Воздействие на элементы КШМ:

а — газовых сил; б — силы инерции Р_j; в — центробежной силы инерции К_r
Силы давления газов. Сила давления газов возникает в резуль­тате реализации в цилиндрах рабочего цикла. Эта сила действует на поршень, и ее значение определяется как произведение пере­пада давления на его площадь: Р_г = (р_г - р₀)F_п (здесь р_г — давление в цилиндре двигателя над поршнем; р₀ — давление в картере; F_п — площадь поршня). Для оценки динамической нагруженности эле­ментов КШМ важное значение имеет зависимость силы Р_г от вре­мени

Сила давления газов, действующая на поршень, нагружает подвижные элементы КШМ, передается на коренные опоры кар­тера и уравновешивается внутри двигателя за счет упругой дефор­мации несущих элементов блок-картера силой , действующей на головку цилиндра (рис. 8.3, а). Эти силы не передаются на опо­ры двигателя и не вызывают его неуравновешенности.

Силы инерции движущихся масс. КШМ представляет собой си­стему с распределенными параметрами, элементы которой дви­жутся неравномерно, что приводит к возникновению инерцион­ных нагрузок.

Детальный анализ динамики такой системы принципиально возможен, однако сопряжен с большим объемом вычислений. Поэтому в инженерной практике для анализа динамики двигате­ля используют модели с сосредоточенными параметрами, создан­ные на основе метода замещающих масс. При этом для любого момента времени должна выполняться динамическая эквивалент­ность модели и рассматриваемой реальной системы, что обеспе­чивается равенством их кинетических энергий.

Обычно используют модель из двух масс, связанных между со­бой абсолютно жестким безынерционным элементом (рис. 8.4).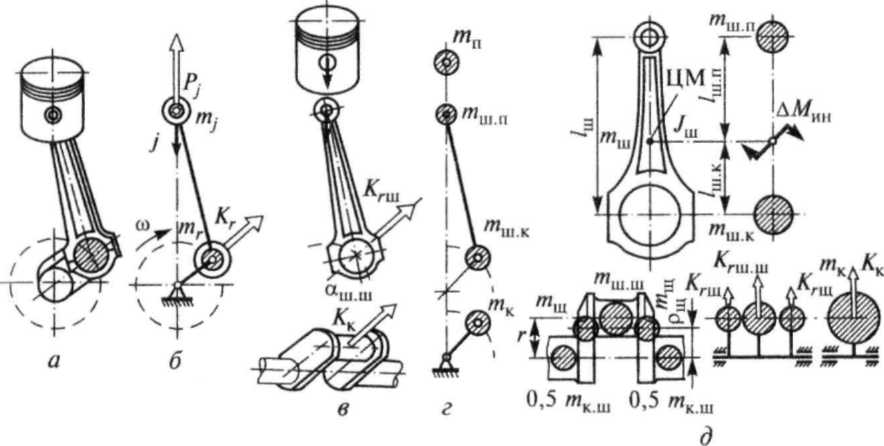



Рис. 8.4. Формирование двухмассовой динамической модели КШМ
Первая замещающая масса m_j сосредоточена в точке сопряжения поршня с шатуном и совершает возвратно-поступательное дви­жение с кинематическими параметрами поршня, вторая m_r рас­полагается в точке сопряжения шатуна с кривошипом и вращает­ся равномерно с угловой скоростью ω.

Детали поршневой группы совершают прямолинейное возврат­но-поступательное движение вдоль оси цилиндра. Так как центр масс поршневой группы практически совпадает с осью поршне­вого пальца, то для определения силы инерции Р_jп достаточно знать массу поршневой группы m_п, которую можно сосредоточить в данной точке, и ускорение центра масс j, которое равно уско­рению поршня: Р_jп = - m_п j.

Кривошип коленчатого вала совершает равномерное вращатель­ное движение. Конструктивно он состоит из совокупности двух половин коренной шейки, двух щек и шатунной шейки. При рав­номерном вращении на каждый из указанных элементов криво­шипа действует центробежная сила, пропорциональная его массе и центростремительному ускорению.

В эквивалентной модели кривошип заменяют массой m_к, от­стоящей от оси вращения на расстоянии r. Значение массы m_к определяют из условия равенства создаваемой ею центробежной силы сумме центробежных сил масс элементов кривошипа: K_к = K_rш.ш + 2K_rщ или m_кrω² = m_ш.шrω² + 2m_щρ_щω², откуда получим m_к = m_ш.ш + 2m_щρ_щω²/r.

Элементы шатунной группы совершают сложное плоскопараллельное движение. В двухмассовой модели КШМ массу шатунной группы m_ш разделяют на две замещающие массы: m_ш.п, сосредоточенную на оси поршневого пальца, и m_ш.к, отнесенную к оси шатунной шейки коленчатого вала. При этом необходимо выполнить следу­ющие условия:

1) сумма масс, сосредоточенных в замещающих точках модели шатуна, должна быть равна массе замещаемого звена КШМ: m_ш.п + m_ш.к = m_ш

2) положение центра масс элемента реального КШМ и заме­щающего его в модели должно быть неизменным. Тогда m_ш.п = m_ш l_ш.к/l_ш и m_ш.к = m_ш l_ш.п/l_ш.

Выполнение этих двух условий обеспечивает статическую эк­вивалентность замещающей системы реальному КШМ;

3) условие динамической эквивалентности замещающей мо­дели обеспечивается при равенстве суммы моментов инерции масс, расположенных в характерных точках модели. Данное условие для двухмассовых моделей шатунов существующих двигателей обыч­но не выполняется, в расчетах им пренебрегают из-за его малых численных значений.

Окончательно объединив массы всех звеньев КШМ в замеща­ющих точках динамической модели КШМ, получим:

массу, сосредоточенную на оси пальца и совершающую возврат­но-поступательное движение вдоль оси цилиндра, m_j = m_п + m_ш.п;

массу, расположенную на оси шатунной шейки и совершаю­щую вращательное движение вокруг оси коленчатого вала, m_r = m_к + m_ш.к. Для V-образных ДВС с двумя шатунами, расположен­ными на одной шатунной шейке коленчатого вала, m_r = m_к + 2m_ш.к.

В соответствии с принятой моделью КШМ первая замещаю­щая масса m_j, движущаяся неравномерно с кинематическими па­раметрами поршня, вызывает силу инерции Р_j = - m_j j, а вторая масса m_r, вращающаяся равномерно с угловой скоростью криво­шипа, создает центробежную силу инерции К_r= К_rш + К_к = - m_rrω².

Сила инерции Р_j уравновешивается реакциями опор, на кото­рые установлен двигатель. Будучи переменной по значению и на­правлению, она, если не предусмотреть специальных мероприя­тий, может быть причиной внешней неуравновешенности двига­теля (см. рис. 8.3, б).

При анализе динамики и особенно уравновешенности двига­теля с учетом полученной ранее зависимости ускорения у от угла поворота кривошипа φ силу Р_j представляют в виде суммы сил инерции первого (Р_jI ) и второго (Р_jII) порядка:



где С = - m_jrω².

Центробежная сила инерции К_r= - m_rrω² от вращающихся масс КШМ представляет собой постоянный по величине вектор, на­правленный по радиусу кривошипа и вращающийся с постоянной угловой скоростью ω. Сила К_r передается на опоры двигателя, вызывая переменные по величине реакции (см. рис. 8.3, в). Таким образом, сила К_r, как и сила Р_j, может являться причиной внешней неуравновешенности ДВС.

Суммарные силы и моменты, действующие в механизме. Силы Р_г и Р_j, имеющие общую точку приложения к системе и единую линию действия, при динамическом анализе КШМ заменяют суммарной силой, являющейся алгебраической суммой: Р_Σ = Р_г + Р_j (рис. 8.5, а).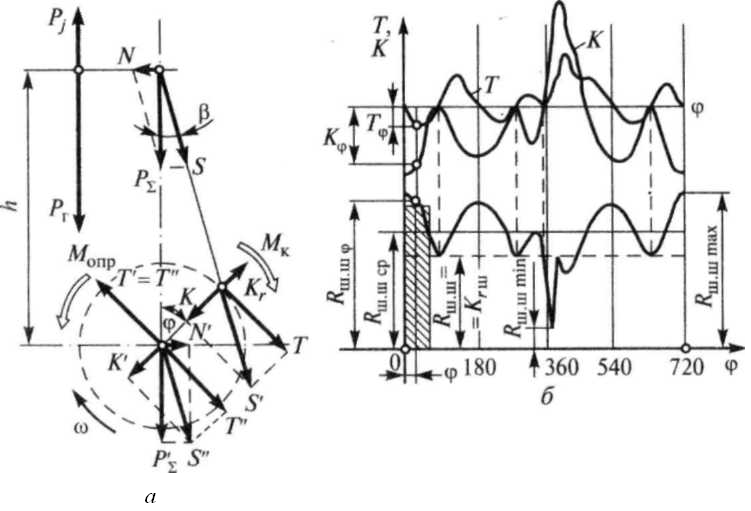