Физ химия курс лекций. Лекция 1 Тема Химическая термодинамика
 Скачать 2.63 Mb. Скачать 2.63 Mb.
|
|
Тема 2. Фазовые равновесия и фазовые диaграммы 2.1. ПРАВИЛО ФАЗ Если в системах нет поверхностей раздела, они называются гомогенными. В гетерогенных системах можно выделить части, различающиеся свойствами и отделенные друг от друга границами раздела. Фазовое равновесие означает одновременное существование термодинамически равновесных фаз в гетерогенной системе, например, двух несмешивающихся жидкостей или воды и льда при температуре плавления. Как уже отмечалось в 1.6, фактором интенсивности фазового перехода является химический потенциал. Самопроизвольный переход компонента i, например, из фазы в фазу произойдет при условии ii . Влияние внешних факторов на фазовые равновесия и переходы определяется правилом фаз Гиббса: C + Ф = К + n, где n - число параметров, которые характеризуют данную систему, например, давление и температура (для газов); Ф - число фаз в системе, которые находятся в устойчивом равновесии (правило фаз распространяется на одно-, двух-, трехфазные и т.д. системы); С - число степеней свободы или максимальное число параметров системы, которые можно в некоторых пределах изменять независимо от других параметров, не изменяя при этом число фаз в системе (по числу степеней свободы системы бывают безвариантные (инваринтные), моновариантные, бивариантные и т.д.); К - число независимых компонентов системы, т.е. минимальное число компонентов, из которых можно создать данную систему. Оно равно общему числу компонентов за вычетом числа связывающих их уравнений. Например, если растворить НСl в воде, то после диссоциации хлороводорода HCl = H+ + Cl- в системе окажется четыре компонента: H2O, HCl, H+, Cl-. Однако концентрации ионов водорода и хлора равны между собой с(H+) = с(Cl-) и определяются количеством хлороводорода и константой химического равновесия реакции при данной температуре (второе уравнение). Поэтому, вычитая из общего числа компонентов (4) число уравнений (2), получим число независимых компонентов, равное двум. По числу компонентов системы могут быть однокомпонентные, двухкомпонентные, трехкомпонентные и т.д. 2.2. ОДНОКОМПОНЕНТНЫЕ СИСТЕМЫ В таких системах фазы состоят из одного вещества, находящегося в различных агрегатных состояниях, т.е. в них не более трех фаз (при С=0), а наибольшее число степеней свободы - 2 (при Ф=1). Эти системы могут быть описаны при помощи двух параметров (n=2), например, давления и температуры. Схема, отражающая области устойчивого состояния фаз, называется фазовой диаграммой или диаграммой состояния (рис. 2.1.). Область, в которой число фаз не изменяется, называется фазовым полем. (I) (II)    р В С Т a р В С Т a  жидкость жидкость ра d• c• b• a • ра d• c• b• a •   b b b bтвердое тело   О пар c c О пар c cА  d d Т время охлаждения Т время охлажденияРис. 2.1. Диаграмма состояния (I) и кривая охлаждения при постоянном давлении (II) для однокомпонент- ной системы Рассмотрим процесс охлаждения системы, состоящей вначале из пара, при постоянном давлении (n=1): изобара abcd на рис.2.1 (I)при р=ра. В точке а С= К+n-Ф=1+1-1=1*. Это означает, что фазовый состав системы в области точки а (пар) при изменении температуры в небольших пределах не изменяется. Но если, например, охладить систему более существенно, то система из точки а постепенно перейдет (по кривым ab (II) иab(I)) в точку b, где начинается и происходит конденсация пара в жидкость. При этом в системе в равновесии находятся две фазы: С=1+1-2=0. Температура не будет изменяться, пока весь пар не сконденсируется в жидкость по кривой bb (II) и в точке b(I). Отвод теплоты при этом компенсируется выделяющейся в системе теплотой конденсации. Система безвариантна, до перехода в другое фазовое поле (жидкость). Далее жидкость охлаждается в соответствии с кривой bc(система моновариантна) до температуры кристаллизации в точке с. Пока вся жидкость не превратится в лед, система остается безвариантной, температура не изменяется (сс). Далее следует охлаждение твердого тела ( сd(II) и сd(I) ). Проведя процесс охлаждения системы (II) при постоянном давлении ра, мы получили две точки на фазовой диаграмме (I): b и с. Построив ряд других кривых охлаждения при других давлениях, мы получим другие точки, совокупности которых образуют кривые ОС и ОВ. Если давление снижать до величин, которые ниже давления в точке О, то будет происходить процесс десублимации пара, минуя жидкое состояние. На кривых охлаждения при этом будет только по одному участку с постоянной температурой. Таким образом будет построена кривая ОА. Кривые ОА, ОС, ОВ соответствуют двухфазным равновесиям и отражают соответственно зависимости температуры возгонки твердого тела, кипения жидкости и плавления твердого тела от давления. В этих случаях один параметр можно изменять независимо, а другой должен измениться в соответствии с первым, чтобы обе фазы оставались в устойчивом равновесии вдоль соответствующих кривых. Если система характеризуется значениями давления и температуры, которые лежат в пределах фазового поля, то оба параметра можно изменять в определенных пределах, и в устойчивом равновесии будет находиться одна фаза. Точка О называется тройной точкой. В ней существует три фазы – жидкая, твердая и пар. В соответствии с правилом фаз число степеней свободы в ней равно нулю, и для каждого вещества тройная точка может быть только одна (для воды её координаты в отсутствии воздуха 0,01 С и 610 Па, а в присутствии воздуха при 1 атм три фазы находятся в равновесии при 0 оС с тем же парциальным давлением пара – 610 Па). Если координата давления тройной точки для вещества лежит ниже атмосферного давления, то вещество при нагревании будет сначала плавиться, а затем кипеть при соответствующей температуре. Если координата давления тройной точки лежит выше атмосферного давления, то вещество при нагревании будет сублимировать при температуре возгонки (например, сухой лед). Наибольший интерес представляет наклон кривых на фазовых диаграммах: где Тф - температура фазового перехода, К;  ln p = (- Hф/RTф ) + const . (2.2) Э 4 т.кип.(станд.) 3 2 жидк. фаза тв. фаза 1 0 -0,5 2 3 4 103/Т  то уравнение линейной зависимости ln p от 1/Т, что и подтверждается экспериментальными данными как для испарения, так и для возгонки (например, рис.2.2 для воды). то уравнение линейной зависимости ln p от 1/Т, что и подтверждается экспериментальными данными как для испарения, так и для возгонки (например, рис.2.2 для воды).                 Рис.2.2. Зависимость логарифма давления пара воды от значений (1/Т)∙103, соответствующая преобразованному (2.2) в уравнение: Константа интегрирования в (2.2) равна первому слагаемому при р = 1 атм. По этому уравнению кривые, например, ОА и ОС рис.2.1 могут быть построены на основании известных данных о теплотах сублимации и испарения. И наоборот, по графикам ln p = f(1/T) можно определить теплоты фазовых переходов (по тангенсам углов наклона прямых: Если вещество в твердом состоянии может существовать в нескольких полиморфных модификациях, то его диаграмма состояния усложняется. Рассмотрим это на примере серы, которая имеет две твердые кристаллические модификации: ромбическую S(ром) и моноклинную S(м) (диаграмма рис. 2.3). 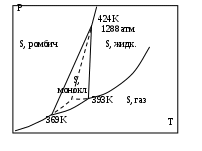 Рис. 2.3. Диаграмма состояния серы На диаграмме видны три тройные точки, соответствующие равновесиям в трехфазных состояниях. Видно также как вещество может существовать в нескольких кристаллических формах, и при этом имеется температура перехода, выше которой устойчивой является одна модификация, а ниже - вторая. Если при температуре перехода превращение модификаций самопроизвольно протекает как в прямом, так и в обратном направлениях, то такой переход называется энантиотропным, например, как в случае серы. В некоторых случаях переход осуществляется только при изменении температуры в одном направлении. Такой переход встречается реже и называется монотропным. Примером является переход белого фосфора в красный. 2.3. ФАЗОВЫЕ РАВНОВЕСИЯ В ДВУХКОМПОНЕНТНЫХ СИСТЕМАХ Фазовая диаграмма для двухкомпонентной системы в общем случае будет трехмерной, т.к. могут изменяться: давление, температура, состав. Для жидкостей и твердых тел давление можно исключить из числа переменных, тогда С+Ф = К+n = 2+1 = 3, а наибольшее число фаз в системе равно трем; диаграмма состояния будет двумерной в координатах "Т - состав". ЛЕКЦИЯ 8 2.3.1. Равновесие кристаллы - жидкость Рассмотрим вначале систему, компоненты которой не образуют друг с другом химических соединений, неограниченно растворимы друг в друге в случае жидкого состояния одного из компонентов, но нерастворимы друг в друге в твердых состояниях. Например, систему: вода – соль (рис.2.4). Чистая вода в виде льда плавится при 273,15 К. Введение в воду растворяющегося вещества повышает ее энтропию и понижает ее химический потенциал (действительно, по (1.23) (I) (II)   Т, К Т Т, К Т  К К  • а' А • а • а' А • а   М L М L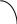 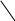 273 • б΄ N • б 273 • б΄ N • бВ C   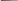 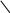 Е с' F с • •d Е с' F с • •dх' • Д • х Н2О массовые доли соль время охлаждения Рис. 2.4. Диаграмма состояния (I) и кривая охлаждения (II) с постоянной скоростью системы вода – соль В фазовом поле А, соответствующем жидкому раствору соли в воде, имеются две степени свободы, т.е. можно одновременно изменять и состав, и температуру. Следовательно, при охлаждении раствора его состав не изменяется (например, состав раствора в точке а'). При некоторой температуре кривая охлаждения (II) достигает точки б, которой на диаграмме соответствует точка б' пересечения прямой а'х' с кривой кристаллизации воды (или плавления льда при нагревании), называемой линией ликвидуса (от латинского слова "ликвидус" – жидкий). В этой точке начинают выпадать кристаллы льда. Теплота кристаллизации воды при этом компенсирует частично потерю системой теплоты охлаждения, и кривая охлаждения понижает свой наклон (бс). Указанному участку кривой охлаждения соответствует отрезок линии ликвидуса б΄с΄, вдоль которого в каждой точке сохраняются равновесные состояния системы с одной степенью свободы и двумя фазами – жидкой и твердой. При этом твердая фаза – это лед, а состав раствора изменяется в соответствии с кривой ликвидуса. В точке с΄ начинает кристаллизоваться соль и одновременно находятся в равновесии три фазы: раствор, лед и соль (эвтектика). При дальнейшем охлаждении системы кристаллизуются вода и соль при неизменной температуре и постоянном составе раствора, число степеней свободы равно нулю (горизонтальный участок кривой охлаждения cd). Кривая, ниже которой существуют только твердые фазы, называется кривой солидуса (от латинского "солидус" - твердый). В данном случае это прямая EF, параллельная оси состава. Эвтектика представляет собой смесь мельчайших кристалликов воды и соли. Характерным является то, что эвтектика всегда обогащена более легкоплавким компонентом. Сходство эвтектики и чистого компонента состоит в том, что они кристаллизуются при постоянной температуре. Однако при изменении давления у эвтектики изменяется не только температура плавления, но и состав. Кроме того при кристаллизации чистого компонента состав твердой и жидкой фаз одинаков, а при кристаллизации эвтектики состав жидкой фазы отличается от состава каждой из равновесной с ним твердых фаз. Рассматриваемая диаграмма состояния системы вода – соль имеет также фазовое поле В, в котором система содержит частицы льда и жидкий раствор соли в воде. В фазовом поле С система содержит твердые частицы соли и жидкий раствор соли в воде. В фазовом поле Д система состоит только из твердых частиц соли и льда. Линии ликвидуса и солидуса соответствуют равновесным состояниям твердых фаз и жидких растворов. Фазовый состав системы в любой точке полей В и С диаграммы можно определить, проведя через эту точку прямую, параллельную оси абсцисс, до пересечения ее с линией ликвидуса и одной из ординат. При этом на состав твердой фазы укажет ордината, а состав раствора будет соответствовать точке пересечения параллельной прямой с линией ликвидуса. Количества обеих фаз можно определить по правилу рычага: они соотносятся между собой так же, как длины отрезков, на которые рассматриваемая точка диаграммы делит прямую, параллельную оси абсцисс (длины противоположных плечей рычага). Например, если при охлаждении раствора, состав которого соответствовал точке К, система пришла в точку N, то параллельная оси состава пунктирная прямая ML точками М и L укажет на ее фазовый состав: М – раствора, L – твердой фазы – соли. При этом масса раствора будет так относиться к массе твердой фазы, как длина отрезка NL относится к длине отрезка MN. Аналогично диаграмме состояния системы вода – соль выглядят диаграммы состояния металл – металл при условии их растворимости в жидком состоянии (в расплавах) и нерастворимости в твердом состоянии. Например, на рис.2.5 представлены кривые охлаждения и диаграмма состояния системы кадмий – висмут. Видно, что когда охлаждается жидкость, состоящая из одного компонента, график зависимости температуры от времени имеет почти постоянный наклон. Однако при температуре кристаллизации кривая охлаждения переходит в горизонтальную прямую линию, если охлаждение производится достаточно медленно. Остановка на кривой охлаждения является результатом выделения теплоты в процессе затвердевания жидкости. Когда охлаждается раствор, то при температуре начала кристаллизации одного из компонентов наклон кривой уменьшается, что обусловлено выделением теплоты при постепенной кристаллизации твердого вещества по мере охлаждения раствора, а также изменением теплоемкости системы. Такие изменения наклона (точки перегиба) видны на кривых охлаждения сплавов, содержащих 0,2 и 0,8 кадмия. Кривые имеют и горизонтальные участки – в обоих случаях при 140 оС. При этой температуре твердые кадмий и висмут выпадают вместе, горизонтальный участок F и точка К при 140 оС; таким образом, этот состав является эвтектическим. Температуры появления новых фаз, найденные по перегибам кривых охлаждения, затем переносят на диаграмму температура-состав, как показано в правой части рис.2.5. В области выше JKL существует одна жидкая фаза, и С=К-Ф+п=2-1+1=2. Вдоль линии JK выкристаллизовывается висмут, а вдоль LK – кадмий. Следовательно, вдоль линии JK и в области под нею вплоть до эвтектической температуры К имеются две фазы – твердый висмут и раствор, состав которого определяется температурой. Поскольку С=2-2+1=1, система моновариантна. Если указать одну из переменных, т.е. температуру или состав жидкой фазы, то другую переменную можно найти на линии JK. Вдоль линии KL и в области под ней также имеются две фазы – твердый кадмий и раствор; соответственно этому С=1. В эвтектической точке К сосуществуют три фазы – твердый висмут, твердый кадмий и раствор, содержащий 0,4 кадмия. Здесь С=2-3+1=0; таким образом, система в этой точке инвариантна. Существуют только одна температура и один состав раствора, при которых эти три фазы могут находиться в равновесии при данном постоянном давлении. Область ниже эвтектической температуры К двухфазная, в ней присутствуют твердые висмут и кадмий; С=2-2+1=1. Для полного описания состояния системы при данном постоянном давлении нужно указать лишь температуру. Отношение висмута к кадмию может изменяться, но здесь есть только чистый висмут и чистый кадмий, и поэтому нет необходимости указывать концентрации. 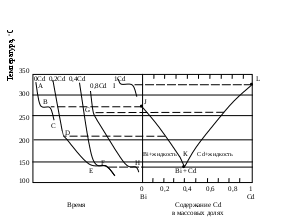 Рис.2.5. Кривые охлаждения и фазовая диаграмма температура-состав для системы висмут – кадмий В некоторых случаях компоненты бинарных систем могут образовывать между собой химические соединения, плавящиеся без разложения на другое твердое вещество и жидкую фазу. В таких случаях на диаграмме состав – температура появляется максимум, как показано на рис.2.6 для системы цинк-магний, и говорят, что это соединение плавится конгруэнтно. Точка на оси составов, соответствующая максимуму температуры, представляет состав соединения. Если концентрация выражена в мольных долях, то такие максимумы появляются при содержании одного из компонентов, равном 0,5; 0,33; 0,25 и т.д., что соответствует целочисленным отношениям компонентов – 1:1, 1:2, 1:3 и т.д. Диаграмма на рис.2.6 похожа на две помещенные рядом диаграммы уже рассмотренного типа, правда они несколько различаются. В данном случае кривая жидкости имеет горизонтальную касательную в точке плавления соединения MgZn2, тогда как в точках плавления чистых компонентов наклон не равен нулю. Это значит, что если в какой-то системе А-В существует конгруэнтно плавящееся соединение АВ, то добавки очень малых количеств А или В не будут понижать его точку плавления (или точку замерзания). Если компоненты бинарной системы образуют химическое соединение, плавящееся с разложением, то говорят, что это соединение плавится инконгруэнтно. В таком случае при нагревании системы до определенной температуры вместо плавления происходит разложение соединения на другое твердое соединение и раствор. 700 Жидкость 650 оС J Е 600 С 590 оС F H G 500 MgZn2 K Mg + 410 оС + раствор MgZn2 + раствор A B раствор 380 оC Zn + 300 раствор L D Zn + MgZn2 MgZn2 + Mg 200 M I 0 0,2 0,4 0,6 0,8 1 Zn Содержание Mg, мольн. доли Mg                  Рис. 2.6. Диаграмма температура – состав с максимумом для системы цинк - магний Такая точка плавления, называемая инконгруэнтной, изображена на рис.2.7, который представляет часть фазовой диаграммы для системы сульфат натрия – вода. 100 D Жидкость Жидкость + Na2SO4 Na2SO4∙10H2O C 32,38 oC A Жидкость + 0 B Na2SO4 ∙ 10H2O -1,286 Na2SO4 + лед + Na2SO4 ∙ 10H2O Na2SO4 ∙ 10H2O 0 0,05 0,1 0,15 Содержание Na2SO4, мольн. доли               Рис.2.7. Часть фазовой диаграммы для системы Na2SO4 - H2O, показывающая инкогруэнтное плавление Na2SO4∙10H2O с образованием ромбического безводного Na2SO4 Если нагревать чистый Na2SO4∙10H2O, то при 32,38 оС он превращается в безводный Na2SO4 и раствор состава С. Линия ВС показывает растворимость Na2SO4∙10H2O в воде, а линия СD – растворимость Na2SO4 в воде. Рис. 2.7 объясняет, почему происходит нарушение непрерывности на кривой BCD для сульфата натрия в воде. Когда три фазы – Na2SO4, Na2SO4∙10H2O и насыщенный раствор – находятся в равновесии, система инвариантна. В ряде случаев компоненты бинарных систем могут быть неограниченно растворимы друг в друге как в жидком, так и в твердом состоянии. Пример диаграммы такой системы показан на рис. 2.8 для компонентов: золото-платина. Две линии на этой диаграмме дают состав жидких (верхняя линия) и твердых (нижняя линия) растворов, находящихся в равновесии. При анализе таких диаграмм следует помнить, что жидкая фаза богаче тем компонентом смеси, который имеет более низкую точку плавления. В области над верхней линией на оба металла находятся в виде жидкого раствора, а под нижней линией – в виде твердого раствора. Верхняя кривая представляет собой кривую затвердевания жидкости, а нижняя – кривую плавления твердого раствора. Пространство между двумя кривыми является областью равновесных смесей двух растворов – жидкого и твердого. Например, смесь, содержащая 0,5 золота и 0,5 платины, в момент равновесия при 1400 оС будет состоять из двух фаз: твердого раствора, содержащего 0,7 платины, и жидкого раствора, содержащего 0,28 платины. Если бы исходная смесь содержала 0,6 платины, то при 1400 оС образовывались бы те же два раствора, твердый и жидкий, того же состава, т.е. содержащих 0,7 и 0,28 платины, но количество твердого раствора в соответствии с правилом рычага, было бы больше, чем в первом случае. 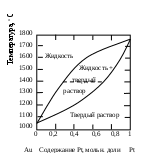 Рис. 2.8. Фазовая диаграмма для системы золото-платина, образующей твердые растворы 2.3.2. Равновесие пар - жидкий раствор нелетучего вещества Французский физико-химик Ф.М. Рауль в 1884 году экспериментально установил, что для идеальных растворов при постоянной температуре давление насыщенного пара растворителя над бинарным раствором (р) меньше чем над чистым растворителем (ро). При этом он нашел соотношение, котрое носит название закона Рауля: р=роX, (2.3) где X - мольная доля раствoрителя в растворе. Давление насыщенного пара растворителя над раствором равно произведению его давления над чистым растворителем на его мольную долю в растворе. В настоящее время (2.3) выводится теоретически из равенства химических потенциалов растворителя в растворе (Р ) и в насыщенном паре (п): Р = п. (2.4) Действительно, если продифференцировать равенство (2.4) с учетом (1.128) и (1.129), то получится следующее равенство: dln p = dln X. Если далее провести интегрирование последнего равенства в пределах от давления пара растворителя над чистым растворителем ро до давления над раствором р и соответственно от мольной доли растворителя в чистом растворителе Хо=1 до его мольной доли в растворе Х, то получается соотношение (2.3), т.е. закон Рауля: ln p - ln pо = ln X - ln Xо, т.к. ln Xо = 0, то p / pо = X или p = pоX . Сумма мольных долей растворителя и растворенного вещества (Xв) бинарного раствора равна 1 (или X = 1-Xв), поэтому вместо последнего равенства вначале получим: р = рo(1- Xв) или р = ро – роXв,откуда следует: ро – р = роXв или Δр/ро = Xв. (2.5) Другими словами, относительное понижение давления пара растворителя над бинарным раствором равно мольной доле растворенного вещества. Формулы (2.3) и (2.5) отражают два способа выражения закона Рауля. Поскольку мольная доля растворителя в растворе всегда меньше единицы, давление его пара над раствором всегда меньше давления его пара над чистым растворителем. Чем более концентрированный раствор, тем значительнее снижение давления пара растворителя. Давление пара растворителя над раствором относится к коллигативным свойствам растворов, т.е. к таким свойствам, которые не зависят от природы веществ, а зависят только от количеств их частиц. 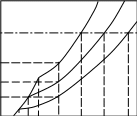 р р0,1013 МПа А • А'• А"• ро В• р′ О• ● В′ р″ О″•О′• • В″ Рис. 2.9. Зависимость давления пара растворителя над раствором и температуры кипения и замерзания раствора от концентрации растворенного вещества: ОА – чистый растворитель; О'А' – разбавленный раствор О"А" – более концентрированный раствор ЛЕКЦИЯ 9 В случае бинарных растворов нелетучих веществ давление пара определяется только растворителем и по (2.3) оно меньше ро. Поэтому для достижения точки кипения (когда давление насыщенного пара жидкости равно давлению окружающей среды, например атмосферному – 0,1013МПа) растворы нужно нагревать до более высоких температур, чем температура кипения чистого растворителя (рис.2.9). Видно, что кривая зависимости р(Т) с ростом концентрации (Хв) смещается вниз (точки В, В', В"), хотя профиль ее остается практически неизменным, а температура кипения (Ткип) при этом возрастает (точки А, А', А"). Рауль экспериментально установил соотношение зависимости увеличения температуры кипения растворов (ΔТкип) от их концентрации: Tкип = Ткип – Ткип(о) = Кэ b, (2.6) где Ткип – температура кипения раствора, Т кип(о) – температура кипения растворителя , b – моляльная концентрация раствора, Кэ – эбуллиоскопическая постоянная, характеризующая только растворитель (для воды Кэ = 0,52кг∙К/моль) и показывающая, чему равно ∆Ткип при b = 1 моль/кг. Поэтому все растворы различных неэлектролитов в одном и том же растворителе при одинаковой концентрации (b) кипят при одной и той же температуре. А в случае упаривания растворов с ростом их концентрации возрастает их температура кипения. В настоящее время уравнение (2.6) выведено теоретически и Кэ в нем имеет следующее значение: |

 (2.7)
(2.7) (2.9)
(2.9)
 а) б) в)
а) б) в)
 4
4



 2 2 1 2 5
2 2 1 2 5 

 3 3 3
3 3 3



 Т р
Т р
 6 •
6 •


 Т(В) р(А)
Т(В) р(А)
 Т1 4 р(В) Т(А) 2 ж •1 п
Т1 4 р(В) Т(А) 2 ж •1 п • •
• •