Физ химия курс лекций. Лекция 1 Тема Химическая термодинамика

• Название: Лекция 1 Тема Химическая термодинамика
• Дата: 30.04.2023
• Размер: 2.63 Mb.
• Имя файла: Физ химия курс лекций.doc
• Тип: Лекция; #1098252
• страница: 4 из 15

Рис 1.9. Энтальпийная диаграмма образования оксида углеродаIV

1.2.4. Теплоты растворения

При растворении веществ теплота может поглощаться или выделяться. В общем случае количество теплоты растворения зависит от концентрации полученного раствора. Интегральная теплота растворения определяется как изменение энтальпии при растворении одного моля вещества в n молях растворителя. Процесс растворения можно представить в виде химического уравнения:

НС1(г) +5Н₂О(ж) = НС1 в 5Н₂О; ΔН°_р-я = – 64,05 кДж , (1.62)

где «НС1 в 5Н₂О» означает раствор 1 моля НС1 в 5 молях Н₂О.

Зависимость интегральных теплот растворения NaCl, NaOH и НCl от количества воды показана на рис. 1.10.

В записях, подобных (1.62), употребляется также символ «aq»,
обозначающий водный раствор, разбавленный настолько, что
дальнейшее разбавление не сопровождается тепловым эффектом. Например:

НС1 (г) + aq = HCl(aq) , ∆Н^о_р-я = – 75,14 кДж . (1.63)

Когда растворяемое вещество и растворитель химически
подобны и при растворении не возникает осложнений, связанных с
ионизацией или сольватацией, теплоту растворения можно считать
приблизительно равной теплоте плавления растворяемого вещества. Однако чаще всего указанные осложнения при растворении бывают. Например, в кристаллической решетке хлорида натрия положительные ионы натрия и отрицательные ионы хлора испытывают сильное взаимное притяжение. Энергия, необходимая для их разделения, настолько велика, что такие неполярные
растворители как бензол и четыреххлористый углерод не
растворяют хлорид натрия. Растворители подобные воде, имеющие
большие значения диэлектрической постоянной и дипольных
моментов молекул, растворяют ионные кристаллы, и NaCl, в
частности. Их молекулы сильно притягиваются как к ионам натрия
так и к ионам хлора. В результате происходит сольватация (образование вокруг ионов оболочек из полярных молекул воды, которые называют в общем случае сольватными) ионов, которая сопровождается значительным уменьшением энергии системы (выделением энергии). Если энергия, требуемая для отрыва ионов от кристалла, близка по значению к энергии сольватации, как, например, в случае растворения NaCl в воде,то значение ∆Н_р-я для суммарного процесса близко к нулю. При растворении NaCl в воде при 298К наблюдается лишь небольшое охлаждение раствора, а величина ∆Н_р-я
положительна. В случае растворения веществ в воде их сольватация
называется гидратацией.




+4

+2 NaCl

0

-2

-4

-6

-8 NaOH

10

12

14

16 HCl

18

0 5 10 15 20 25 30 35 40 45

Число молей Н₂О на 1 моль растворенного вещества




Рис.1.10.Интегральные теплоты растворения соединений при 298 К

Интегральная теплота разбавления раствора от моляльности b₁ до моляльности b₂ определяется как количество теплоты, которое поглощается или выделяется при разбавлении некоторого объема раствора с концентрацией b₁, содержащего 1 моль растворенного вещества, чистым растворителем до концентрации b₂.

Интегральные теплоты растворения, теплоты разбавления и теплоты реакций в растворах могут быть рассчитаны из табулированных значений теплот образования веществ в растворенном состоянии. В таких расчетах можно пренебречь энтальпией образования воды, если в обе части уравнения химической реакции входит одинаковое число молей воды. Энтальпия образования воды в водном растворе принимается равной энтальпии образования чистой воды. Это допущение так же произвольно, как и приравнивание к нулю энтальпий образования элементов.

ЛЕКЦИЯ 4 1.2.5. Зависимость тепловых эффектов химических

реакций и процессов от температуры

Уравнение химической реакции в общем виде можно представить следующим образом:

₁А₁ + ₂А₂ = ₃А₃ + ₄А₄,

где _i – стехиометрические коэффициенты, А₁ и А₂ – реагенты, А₃ и А₄ – продукты реакции. Тогда изменение энтальпии данной реакции (∆Н) при соответствующей температуре можно вычислить по (1.56), вычитая сумму энтальпий исходных веществ из суммы энтальпий продуктов реакции (в частности, при стандартной температуре) –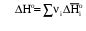

, (1.64)

где ₃ и ₄ положительны, а ₁ и ₂ отрицательны. Поскольку энтальпии химических реакций зависят от температуры, то скорость изменения  с изменением температуры можно вычислить, дифференцируя уравнение (1.64) по температуре при постоянном давлении:

. (1.65)

Учитывая по (1.40), что , вместо (1.65) получим:

. (1.66)

Полученное уравнение называется уравнением Кирхгофа. Оно показывает, что при постоянном давлении изменение энтальпии реакции в результате повышения температуры реакционной системы на один градус равно изменению ее теплоемкости.

Уравнение (1.66) можно проинтегрировать от Т₁ до Т₂ и получить соотношение между изменениями энтальпии реакции при указанных температурах: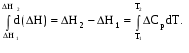

(1.67)

Это уравнение позволяет вычислить ΔΗ реакции при заданной температуре, если известны ΔΗ реакции при другой температуре и значения 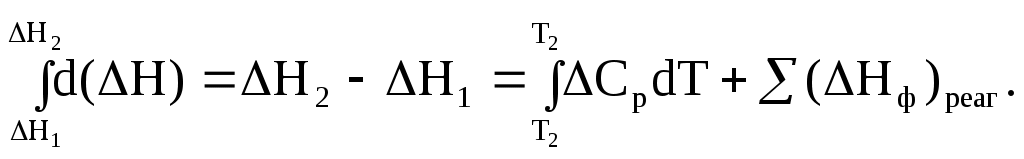реагентов и продуктов реакции в промежуточной области температур. Им удобно пользоваться в тех случаях, когда известны эмпирические зависимости С_р,i от температуры – (1.50). Уравнение (1.67) справедливо только при условии, что в области температур от Т₁ до Т₂ не происходит фазовых превращений. Для учета изменений энтальпии в случае фазовых превращений (∆Н_ф – плавления, испарения, кристаллизации, конденсации)в промежутке ΔΤ в уравнение (1.67) необходимо вводить дополнительные члены:

(1.68)

Если теплоемкости продуктов реакции больше теплоемкостей исходных веществ, то для экзотермической реакции ( тепловой эффект реакции с повышением температуры падает, а для эндотермической реакции ( - растет. Если С_р, то наблюдаются обратные зависимости. В случае равенства теплоемкостей продуктов и исходных веществ тепловой эффект реакции не зависит от температуры. В общем случае зависимости энтальпий реакций от Т могут иметь экстремумы в точках, где теплоемкости продуктов и исходных веществ равны, например, как показано на рис. 1.11.

С_р,i 

исходные

вещества

продукты продукты

Т₁ Т Т₁ Т
Рис.1.11. Общий вид зависимостей от температуры С_р,i реагентов

и продуктов и ΔН реакции
Так как на кривых ∆Н = f(Т) могут быть экстремумы, то их нельзя экстраполировать за пределы опытных данных.

При решении уравнения (1.67) чаще всего берут Т₁=298 К, а изменение энтальпии реакции вычисляют по закону Гесса, используя табличные значения энтальпий образования веществ. Если теплоемкости в рассматриваемом интервале температур постоянны, то получают:

Н₂ = H₁ + C_р (T₂ - Т₁). (1.69)

Например, вычислим, какое количество теплоты выделится при замерзании одного моля переохлажденной воды при постоянном давлении 1 атм и температуре 263 К:

Н₂О(ж) → Н₂О(к).

По табличным данным имеем следующие значения: (Н₂О) (кристаллизации) при 273К = – 6,009 кДж/моль, (Н₂О(к)) = 36,9Дж/(моль∙К), (Н₂О(ж)) = 75,31 Дж/(моль∙К). Для рассматриваемого процесса в соответствии с (1.67) необходимо вычислить при Т₂=263 К:



где – энтальпия кристаллизации одного моля воды при Т₁ = 273 К. Так как промежуток ΔТ мал, то можно предположить, что в нем (Н₂Ож) и (Н₂Ок) постоянны и можно вычислить по (1.69):



Действительно, в соответствии с законом Гесса рассматриваемый процесс может быть проведен двумя путями (а) или (б) по представленной схеме:

Т₂=263 К (а) Т₂=263 К

Н₂О_(ж) Н₂О_(к)


( б)

(б^') (б''')

(б")

Н₂О(ж) Н₂О(к)

Т₁=273 К Т₁=273К

Видно, что энтальпия процесса (а) равна сумме энтальпий стадий (б'), (б'') и (б'''), т.е. энтальпии процесса (б). При этом стадия (б'') проводится при Т₁ (кристаллизация воды при температуре кристаллизации), а стадии (б') и (б''') – это нагревание и охлаждение соответственно жидкой воды и льда, изменения энтальпий в которых легко вычислить по (1.41):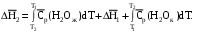



Алгебраически суммируя интегралы, получим: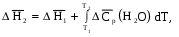



т.е. выражение (1.69). Решим последнее уравнение:

_ _ _ _

ΔН₂ = ΔН₁ + [С_р(Н₂Ок) – С_р(Н₂Ож)] · (Т₂ – Т₁) =

= – 6009 Дж/моль + [(36,9Дж/(моль·К)) – (75,31 Дж/(моль·К))] ·

· (263К – 273К) = – 5625Дж/моль.

В заключение отметим, что если процессы протекают при постоянном объеме, то их тепловые эффекты необходимо вычислять по формулам, аналогичным (1.67) и (1.69), используя значения ΔU и ΔC_V соответственно вместо ΔН и ΔС_р.

1.3. ВТОРОЙ И ТРЕТИЙ ЗАКОН ТЕРМОДИНАМИКИ

Первый закон термодинамики утверждает, что при превращении одной формы энергии в другую общее количество энергии сохраняется. На какие-либо ограничения этого процесса первый закон не указывает. Однако известно, что многие процессы характеризуются самопроизвольным или естественным течением, другие процессы самопроизвольно протекать не могут, и как раз с этим связан второй закон термодинамики. Например, газ расширяется в пустоту, но обратный процесс не протекает никогда. Хотя формально это не нарушило бы первый закон. Он не был бы нарушен и в том случае, если бы стержень с первоначально одинаковой температурой по всей длине стал горячим на одном конце и холодным на другом. Но мы знаем, что на практике этого никогда не случится. Второй закон устанавливает критерий, позволяющий предсказать, может ли данный процесс идти самопроизвольно или нет, и поэтому он имеет важное значение для химии.

1.3.1. Обратимые и необратимые, самопроизвольные и

несамопроизвольные процессы

Обратимым называется процесс, который в любой момент времени можно заставить протекать в обратном направлении, изменив какую-нибудь независимую переменную на бесконечно малую величину. Рассмотрим в качестве примера процесс теплообмена между двумя закрытыми системами I и II (рис.1.12). В нем независимой переменной является температура. По схеме рисунка система I представляет собой емкость (1), в которой при температуре 273,15 К находятся в равновесии вода (3) и кусок льда (2) в количествах, равных соответственно а и в. При этой температуре не будет происходить ни плавления льда, ни кристаллизации воды. На молекулярном уровне рассматриваемое состояние равновесное и динамическое, то есть подвижное, - за каждую единицу времени какое-то количество молекул льда переходит в воду (плавится) и такое же количество молекул жидкой воды переходит в лед (кристаллизуется). Подобные состояния систем могут быть записаны в виде уравнений. Например, для системы I при Т = 273,15К будет выполняться следующее уравнение:


1

2
3
4
5


6


4
H₂O(к) ⇄ Н₂О(ж). (1.70)


I










II



Рис. 1.12. Схема теплообмена между закрытыми системами I и II:

1- емкость с водой и льдом; 2- лед; 3 – вода;

4 – тепловая изоляция; 5 – пробное тело;

6 – емкость с теплоносителем

Система II представляет собой тепловой резервуар, теплоносителем которого могут быть различные вещества, включая воду. Пробное тело (5) – это небольшой металлический шарик, укрепленный на ручке, изготовленной из полимерного материала, плохо проводящего теплоту.

Если температура теплоносителя системы II будет незначительно выше 273,15К, то, касаясь пробным телом неизолированных участков вначале системы II, а затем системы I, мы перенесем от системы II системе I порцию теплоты dq. Эту операцию можно повторять многократно. Каждая порция теплоты dq будет увеличивать на бесконечно малую величину температуру воды в емкости (1) на dT, что будет приводить к плавлению бесконечно малой порции льда и образованию из нее такой же бесконечно малой порции воды dn. В последней будет сосредотачиваться (запасаться) теплота dq в виде скрытой теплоты плавления:

. (1.71)

Для того чтобы расплавилось заметное количество льда (например, заштрихованная часть куска льда на рис. 1.12) и образовалось такое же количество воды, описанный процесс теплообмена порциями dq необходимо проводить бесконечно долго (назовем его прямым процессом). При этом все количество переданной от системы II системе I теплоты можно вычислить интегрированием бесконечно малых порций dq по (1.71):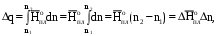

(1.72)

где n₁ и n₂ – соответственно начальное и конечное количества воды в системе I. Это количество теплоты, полученное от системы II в прямом процессе, окажется запасенным в системе I. И если прямой процесс протекал без потерь теплоты в окружающее пространство, то его можно назвать обратимым. Только в обратимом процессе запасается такое количество теплоты, которого достаточно для протекания обратного процесса и возвращения системы к начальному состоянию. Рассматриваемый прямой процесс можно было в любой момент времени повернуть в обратное направление. Мы это сделаем после завершения прямого процесса.

Допустим, что, понизив предварительно температуру теплоносителя системы II до значения, незначительно ниже 273,15 К, мы пробным телом будем касаться вначале системы I, затем системы II. При этом теплота бесконечно малыми порциями dq будет передаваться от системы I системе II. Если такой обратный процесс проводить бесконечно долго, то часть воды в системе I закристаллизуется и, если количество образовавшегося при этом льда будет равно ∆n, то система I передаст системе II такое же количество теплоты ∆q, как в прямом процессе по (1.72):



где штрихом помечены числа молей льда. Для системы I в обратимом процессе выполнится равенство:

∆q(прям.) = – ∆q(обратн.), (1.73)

а после завершения всего цикла она придет к исходному состоянию с количествами воды и льда соответственно а и в при Т = 273,15К.

Если рассмотренные прямой и обратный процессы проводить с заметной скоростью за какой-то конечный промежуток времени, то теплоту от одной системы к другой системе необходимо передавать большими количествами. При этом будут неизбежны потери теплоты в окружение и не выполнится равенство (1.73):

∆q(прям.) ≠ – ∆q(обратн.). (1.74)

В этом случае процесс будет необратимым.

В качестве примера можно рассмотреть реакцию сгорания пропана (бытового газа) в газовой горелке:

С₃Н₈(г)+5О₂(г) = 3СО₂(г)+4Н₂О(г); ∆Нº_р = – 2202 кДж. (1.75)

В этой реакции выделяется теплота (∆Нº_р<0), она экзотермическая и протекает с заметной скоростью. Можно ли повернуть эту реакцию в сторону образования реагентов, изменив температуру реакционной смеси на dТ? Конечно же, это невозможно. Иначе бы мы, поднеся к пламени горелки горячее пробное тело, погасили бы пламя. Эта реакция необратима еще и потому, что протекает с отдачей теплоты окружению.

Итак, обратимые процессы протекают бесконечно медленно и долго, без потерь энергии в окружение. Необратимые процессы протекают с заметной скоростью и с потерями энергии в окружение.

Рассмотрим далее самопроизвольные процессы, то есть процессы, протекающие без воздействия на системы окружения. Давно установлено, что самопроизвольно осуществляются процессы, ведущие к понижению потенциальной энергии систем. Так, камень самопроизвольно скатывается вниз по склону горы и его потенциальная энергия (mgh) при этом понижается. Примером такого же процесса может быть реакция (1.75). В ней энтальпия образования продуктов реакции ∆Hº_прод (потенциальная энергия продуктов) меньше энтальпии образования реагентов ∆Hº_реаг (потенциальной энергии реагентов). Уменьшение потенциальной энергии реакционной системы (1.75) равно:

∆Hº_р = ∆Hº_прод – ∆Hº_реаг = – 2202 кДж.

О реакциях, которые протекают самопроизвольно и с выделением энергии (экзотермические реакции), говорят, что их движущим фактором является энтальпийный фактор (∆Hº_р<0)(при V=const, ΔU^o_p<0).

Исходя из опыта, можно утверждать, что самопроизвольные процессы не идут в обратном направлении. Например, камень не закатывается сам на вершину горы. Процессы, обратные по отношению к самопроизвольным, называются несамопроизвольными. Чтобы вызвать несамопроизвольный процесс, к системе необходимо подвести энергию извне. Очевидно, что нужно совершить работу, для того чтобы закатить камень на вершину горы. А к химической системе (1.75) необходимо подвести энергию в соответствии с первым законом термохимии, для того чтобы она прошла в обратном направлении.

Наряду с самопроизвольными экзотермическими процессами известны самопроизвольные эндотермические процессы. Например: плавление льда при стандартных условиях –

_

Н₂О (к) → Н₂О (ж); ∆Нº = 6,0 кДж/моль ;

растворение хлорида калия в воде –

_

КСl(к) + Вода → КСl(водн); ∆Нº = 19 кДж/моль;

испарение воды –

_

Н₂О (ж) → Н₂О (г); ∆Нº = 44 кДж/моль.

Все три примера имеют одно общее свойство – частицы исходных состояний более упорядочены, чем частицы конечных состояний. Действительно, регулярная структура льда из молекул воды в узлах кристаллической решетки при плавлении заменяется жидкими ассоциатами молекул воды в среде жидкой воды, не имеющей регулярного строения. Растворение хлорида калия также сопровождается разрушением кристаллической решетки и возникновением беспорядочного распределения ионов К⁺ и Сl^¯ в воде. Когда испаряется вода, ассоциаты из ее молекул заменяются отдельными молекулами, движущимися независимо друг от друга в газовой среде. Следовательно, стремление к увеличению неупорядоченности систем является движущим фактором самопроизвольных эндотермических процессов.

Так как изменение величин энтальпии ∆Н (и внутренней энергии ∆U) не дает однозначного ответа на вопрос о возможности самопроизвольного протекания химических реакций и физических процессов, то для этой цели введена еще одна термодинамическая функция, названная энтропией. Энтропия – это термодинамическая функция, характеризующая тепловое состояние систем, а также меру их неупорядоченности. Ее обозначают латинской прописной буквой S.

ЛЕКЦИЯ 5 1.3.2. Энтропия

Так как энтропия S – это функция состояния системы, то это означает, что также, как и внутренняя энергия, энтропия имеет конкретное численное значение, когда система находится в определенном состоянии. Дифференциал энтропии выражается следующим образом:

dS = dq_обр/T, (1.76)

где dq_обр – дифференциал теплоты в обратимом процессе, T – абсолютная температура. Употребление dq_обр вместо dq указывает на то, что q не является функцией состояния, а зависит от пути, по которому осуществляется изменение. Однако для обратимого процесса dq_обр/T представляет собой полный дифференциал. Изменение энтропии, сопровождающее данное изменение состояния не зависит от пути перехода. Изменение энтропии для конечного изменения от состояния 1 до состояния 2 получают интегрированием уравнения (1.76) по обратимому пути:

. (1.77)

Любой обратимый путь между состояниями 1 и 2 даст то же самое значение интеграла.

Подчеркнем, что понятие энтропии является не более сложным, чем понятие внутренней энергии. Действительно, каждая система обладает некоторым свойством, называемым внутренней энергией, причем ее возрастание dU при изменении можно найти, измеряя поглощенную при этом теплоту и вычитая совершенную системой работу. Каждая система также обладает некоторым свойством, называемым энтропией S, причем возрастание энтропии dS можно найти, измерив теплоту, поглощенную системой при обратимом процессе, и разделив ее на температуру T, при которой происходит поглощение теплоты. Следует отметить также, что при изложении термодинамики с применением методов статистической теории показано, что энтропия системы является мерой неупорядоченности ее состояния.

Макроскопические свойства веществ, с которыми имеет дело термодинамика, разделяются на две группы: интенсивные и экстенсивные. Интенсивные свойства не зависят от количества вещества (n) в системе. К ним относятся: температура T, давление p и плотность ρ. Экстенсивные свойства прямо пропорциональны количеству вещества или массе системы, если интенсивные свойства системы поддерживаются постоянными. Экстенсивными свойствами являются объем V и внутренняя энергия U. В данном разделе в термодинамику введено несколько новых экстенсивных свойств. Первое из этих свойств – энтропия S, далее – изохорный потенциал A (свободная энергия Гельмгольца) и изобарный потенциал G (свободная энергия Гиббса). Наряду с этим введено также несколько новых интенсивных свойств: химический потенциал μ и частные производные V_i, U_i, H_i, S_i, A_i, G_i, соответствующих экстенсивных свойств по количеству вещества.