Физ химия курс лекций. Лекция 1 Тема Химическая термодинамика

• Название: Лекция 1 Тема Химическая термодинамика
• Дата: 30.04.2023
• Размер: 2.63 Mb.
• Имя файла: Физ химия курс лекций.doc
• Тип: Лекция; #1098252
• страница: 6 из 15

1.3.8. Изобарный потенциал как критерий

равновесия при постоянной температуре и давлении

При постоянной температуре из уравнения (1.110) получается:

∆G = ΔH – TΔS. (1.119)

Из (1.119) видно, что самопроизвольность процесса при постоянных р и Т зависит от двух членов ∆Н и T∆S. В пользу самопроизвольного процесса говорит отрицательное значение ∆Н или положительное значение ∆S, что означает соответственно уменьшение энергии и увеличение неупорядоченности. Если ∆Н велико, а Т∆S мало, то знак ∆G будет определяться исключительно знаком ∆Н (при ∆Н<0 самопроизвольность процесса определит только энтальпийный фактор). Если Т∆S велико, а ∆Н мало, то знак ∆G будет определяться исключительно знаком ∆S (при ∆S>0 самопроизвольность процесса определит только энтропийный фактор). Так всегда бывает при очень высоких температурах. В других случаях оба члена правой части (1.119) могут играть существенную роль. В любом случае самопроизвольный процесс приводит к минимально возможному значению величины H–TS для системы при постоянных р и Т.

Чтобы иметь наглядное представление о роли Н и TS в определении положения равновесия, рассмотрим испарение твердого вещества в замкнутом пространстве. Если бы действовало только стремление системы достигнуть низкого значения энтальпии (минимальной энергии), то произошла бы полная конденсация пара, так как твердая фаза обладает более низкой энтальпией. Если бы действовало только стремление системы достигнуть высокого значения энтропии (максимальной неупорядоченности), то это привело бы к полному испарению твердого вещества, поскольку газовая фаза обладает более высокой энтропией. Можно вычислить зависимость Н и TS от доли вещества, находящейся в газовой фазе. В общем виде такая зависимость представлена на рис.1.13. С увеличением доли пара энтальпия системы линейно возрастает, но энтропия вначале растет быстрее. Поэтому H–TS имеет минимальное значение, когда некоторая доля вещества представляет собой пар. Это и есть положение равновесия (точка Х_равн).



+ TS H

0

G

-


0 Х_равн 1

Доля пара

Рис.1.13. Термодинамические функции для системы кристалл-пар при постоянных температуре и давлении

Если концентрация в паре ниже равновесного значения, то будет происходить самопроизвольное испарение, если же концентрация выше равновесной, то будет происходить самопроизвольная конденсация. Любой из этих процессов приводит к уменьшению G. Уравнение (1.119) имеет большое значение, потому что ΔН и ΔS можно определить непосредственно в калориметрических измерениях, а затем вычислить ΔG. Изменение изобарного потенциала используется для расчета констант равновесия химических реакций и электродвижущей силы гальванических элементов.

1.3.9. Третий закон термодинамики

Наиболее простую формулировку третьего закона термодинамики дал немецкий физик – теоретик М.К.Э.Л. Планк – энтропия каждого чистого кристаллического вещества при температуре абсолютного нуля равна нулю:

S_o = 0. (1.120)

Следует подчеркнуть, что перед словом «вещество» необходимо ставить прилагательное «кристаллический»,чтобы исключить такие системы как жидкий гелий при атмосферном давлении. Дело в том, что жидкий гелий не находится в состоянии полной упорядоченности даже при абсолютном нуле. Из приведенной формулировки третьего закона следует, что изменение энтропии для кристаллических веществ при всех процессах, происходящих при абсолютном нуле, также равно нулю. Именно в этой формулировке третий закон термодинамики был экспериментально установлен немецким физиком-теоретиком В.Ф. Нернстом в 1906 году.

Первый и второй закон термодинамики оперируют с изменениями энергии и энтропии, третий закон — с их абсолютными значениями. По третьему закону энтропия любого вещества конечна и положительна и ни одна система не может обладать отрицательной энтропией.

Содержание третьего закона более глубоко раскрывается с помощью статистической теории и представлений квантовой теории строения вещества. В 1872 году австрийский физик Больцман первым пришел к заключению о том, что энтропия является функцией только термодинамической вероятности (или мультиплетности) W и что это соотношение должно быть логарифмическим:





S = k lnW, (1.121)

где k – постоянная Больцмана (k = R/N_A). Мультиплетность W равна числу различных способов размещения структурных частиц системы (или вещества) при нахождении ее при данных термодинамических параметрах. В качестве наглядного представления о величине W рассмотрим схему двумерного кристалла (рис.1.14).








а) б)

Р ис.1.14. Схемы двумерных кристаллов из атомов А и В (а) и только из атомов А (б): – атомы А; – атомы В

Допустим, что в узлах кристалла находятся атомы одного и того же элемента – изотопы А и В (а). Энергия взаимодействия между ними одинакова, поэтому независимо от того, в каких узлах и какие атомы находятся, энергия и состояние кристалла при одних и тех же р и Т будут одинаковыми. Допустим также, что при некотором значении Т атомы А и В могут перескакивать вследствие диффузии из одного узла в другой. Вычислим, сколькими способами можно реализовать данное состояние. Очевидно, что два состояния кристалла будут при размещении атомов В по диагоналям кристалла и четыре состояния кристалла будут при размещении атомов В вдоль каждой из сторон кристалла. Всего шесть состояний – это и есть величина W. Значение энтропии такого кристалла будет равно S=1,381·10^-23 Дж/К ln6 = 2,47 ·10^-23 Дж/К. Если бы рассматриваемый кристалл состоял только из атомов А (б), то при абсолютном нуле температуры в этом случае возможно было бы только одно состояние – когда атомы А находятся в узлах кристаллической решетки, то есть W=1. Тогда по формуле (1.121) энтропия равна нулю

S = k ln1 = 0,

что находится в соответствии с третьим законом термодинамики.

Абсолютную энтропию газа при температуре Т можно вычислить, интегрируя dq_обр/Т от 0 К до заданной температуры. Если известны теплоемкости, энтальпия плавления в точке плавления Т_пл и энтальпия испарения в точке кипения Т_кип, то абсолютная энтропия при температуре Т может быть рассчитана по уравнению (1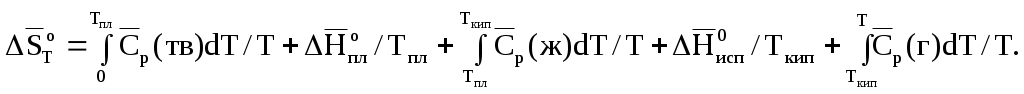.122):

(1.122)

Если твердое тело находится в разных модификациях и их взаимное превращение сопровождается изменением энтальпии, то в сумму (1.121) нужно включить соответствующие энтропии фазовых превращений. Четвертое слагаемое (1.122) представляет собой мольную энтропию испарения. В стандартных условиях в точках кипения для многих жидкостей она постоянна и равна примерно 88кДж/(моль К):

(1.123)

Это уравнение, известное как правило Трутона, полезно для оценки мольной теплоты испарения жидкостей с известными точками кипения.

1.3.10. Химический потенциал

В случае открытых систем в них могут вводиться или из них могут выводиться какие-то вещества. В частности, при протекании химических реакций изменяются числа молей компонентов в системах. В таких случаях энергия Гиббса каждой системы зависит не только от р и Т, но и от количеств веществ, а ее полный дифференциал через частные производные имеет следующий вид:

k

dG = (G/T) dT + (G/p) dp + (G/n_i) dn_i , (1.124)

ⁱ⁼¹

где k – число различных веществ; n_1, n₂, n₃ … n_k – числа молей веществ; n_i – число молей вещества i; j i – это значит, что в производных под знаком суммирования сохраняются постоянными числа молей всех компонентов, кроме i-го. Можно показать, что первые две производные в скобах уравнения (1.124) соответственно равны – S и V. Поэтому вместо (1.124) получим (1.125):

k

dG = – SdT + Vdp + μ_idn_i , (1.125)

ⁱ⁼¹

где величина

μ_i = (G/n_i)_T,p,

называется химическим потенциалом i-го компонента.

Химический потенциал i-го компонента равен приращению энергии Гиббса при добавлении одного моля этого компонента к большому объему системы при постоянных температуре и давлении и неизменных количествах других компонентов. Система должна быть достаточно большой, чтобы от добавления одного моля вещества i ее состав практически не изменился. Химический потенциал чистого вещества равен энергии Гиббса одного моля данного вещества:

(1.126)

При постоянных р и Т вместо (1.125) получим (1.127):

k

dG_p,T = (_idn_i)_p,T . (1.127)

ⁱ⁼¹

Химический потенциал данного компонента в системе зависит как от его концентрации, так и от вида и концентрации других компонентов системы. Только в случае смеси идеальных газов химический потенциал данного компонента (_i) зависит лишь от его концентрации и температуры:

_i  _i  RT ln (p_i /р),

где p_i - парциальное давление в атмосферах компонента i в смеси, _i – стандартный химический потенциал компонента i при Т =298 К и р =1атм. Это уравнение обычно записывают в виде:

_i  _i  RT lnр_i . (1.128)

Однако следует помнить, что в (1.128) р_i фактически заменяет величину p_i /р_i, которая не имеет размерности и поэтому только от нее может быть взят логарифм.

В случае идеального раствора зависимость химического потенциала i-го компонента от его мольной доли в растворе х_i и температуры выражается уравнением:

_i  _i  RT lnх_i , (1.129)

где _i – химический потенциал чистого i-го компонента (при х_i = 1).

Химический потенциал характеризует способность рассматриваемого компонента к выходу из данной фазы путем испарения, растворения, кристаллизации, химического взаимодействия и т.д. При этом переход компонента происходит самопроизвольно из данной фазы (например,(1)), в которой его химический потенциал _i(1) больше, в фазу (2), в которой его химический потенциал _i(2) меньше. Такой переход сопровождается уменьшением химического потенциала этого компонента в фазе (1) и увеличением его в фазе (2). Если в результате установится равновесие, то химический потенциал окажется одинаковым в обеих фазах ('_i(1) = '_i(2)).

ЛЕКЦИЯ 7 1.3.11. Константы равновесия

Химическое равновесие означает неизменность во времени параметров системы. Рассмотрим в общем виде химическую реакцию в газовой фазе, считая газ идеальным (при низких р):

аА + вВ ⇄ сС+dD .

Это равновесие при постоянной температуре характеризуется константой равновесия К_р:

К_р = р^с(С)p^d(D)/ р^а(А) р^в(В), (1.130)

где р(i) – парциальные давления компонентов системы. В случае аналогичного химического равновесия в идеальном растворе константа равновесия имеет следующее выражение:

К_с = с^с(С)c^d(D)/ с^а(А) с^в(В), (1.131)

где с(i) – молярные концентрации компонентов в растворе. Уравнения (1.130) и (1.131) представляют собой выражение закона действующих масс применительно к идеальным газам и разбавленным растворам, установленного эмпирически норвежскими учеными К. Гульдбергом и П. Вааге. В настоящее время уравнения (1.130) и (1.131) выведены теоретически.

Если равновесные системы содержат индивидуальные вещества в конденсированных фазах, то их концентрации и парциальные давления являются постоянными и не входят в правые части (1.130) или (1.131), а учитываются соответствующими значениями констант равновесий.

Если равновесная газообразная система не является идеальной, то в (1.130) вместо каждого давления вводят величину, которая называется фугитивностью или летучестью:

f =  p ,

где  - безразмерный коэффициент фугитивности, зависящий от р и Т. Фугитивность имеет такую же размерность, как и давление. Фугитивность - это такое давление реального газа, при котором газ можно описать по (1.128) и (1.130) как идеальный. Применение f практикуется вместо парциальных давлений при высоких давлениях и низких температурах (до 1 МПа ).

Для перехода от реальных растворов к идеальным введено понятие активности (а):

а = _с с,

где _с - коэффициент активности, зависящий от Т и с. Активность - это такая кажущаяся концентрация, при использовании значения которой реальные растворы можно описать по (1.129) и (1.131). При разбавлении раствора _с стремится к единице, и активность становится равной концентрации.

Связь между константами равновесия для рассмотренной реакции, выраженными через концентрации и активности определяется соотношением:

К_а = К_с ( _с^с (С)γ (D)/ _с^а (А) _с^в (В)) . (1.132)

1.3.12. Равновесия в газовых реакциях и

изотерма химической реакции
Показано, что если реакция протекает в равновесной системе, независимо от ее состава, включающего газы, жидкости, твердые вещества или растворы, то выполняется следующее условие химического равновесия:

_i _i = 0,

где _i– стехиометрические коэффициенты уравнения химической реакции, _i – значения химических потенциалов компонентов, соответствующие равновесному состоянию (ΔG_p,T = 0). Если равновесное состояние не достигнуто, то выполняется уравнение:

ΔG_p,T = _i _i.

Рассмотрим в качестве примера реакцию аА + вВ ⇄сС + dD, протекающую при постоянных давлении и температуре в смеси идеальных газов с начальными неравновесными парциальными давлениями р'(А), р'(В), р'(С), р'(D). В этом случае химический потенциал каждого компонента можно представить по (1.128) следующим образом:

_i =   RT ln р_i .

Тогда:

G = c(C) + d(D)  a (A) - b(B) = c(C) + d(D)

 a (A) b(B) + RT(cln р(C) + dln р(D) – aln р(A) –bln р(B))
или

G = G + RTln . (1.133)

Полученное выражение называется изотермой химической реакции или изотермой Вант-Гоффа. В состоянии равновесия закон действующих масс для данной реакции может быть представлен в следующем виде:



Поскольку при равновесии G = 0, то с учетом (1.133) можно написать:

G = – RT ln К_р (1.134)

или

К_р = exp (– G / RT). (1.135)

По (1.135) видно, что К_р зависит от температуры. Поэтому, изменяя температуру реакционной системы, мы тем самым изменяем и равновесные концентрации компонентов так, что изменяется значение константы равновесия. В отсутствии равновесия по (1.133) и (1.134) имеем:

. (1.136)

1.3.13. Равновесия реакций, протекающих в растворах

Аналогично выражению (1.135) можно получить (1.137) для равновесия аА + вВ ⇄ сС + dD в жидкой фазе:

, (1.137)

где а(i) – активности компонентов. В разбавленных растворах коэффициенты активности компонентов стремятся к единице, и в выражение для константы равновесия можно ставить концентрации, а не активности. В общем же случае концентрационная константа равновесия К_с оказывается не постоянной величиной. В отсутствии равновесия и значений _i,, стремящихся к единице, будем иметь:

, (1.138)

где c'(i) – неравновесные молярные концентрации веществ.

1.3.14. Изобара и изохора химической реакции

Константы равновесий зависят от температуры, например (1.135). Представим изменение энергии Гиббса в выражении (1.134) в виде изменения энтропии и энтальпии реакции:

Н° – ТS° = – RT ln К_р .

Откуда получим:

ln К_р = – Н°/RT + S°/R. (1.139)

По (1.139) график зависимости ln К_р от 1/Т в некотором интервале температур должен выражаться прямой линией, тангенс угла наклона которой к оси абсцисс равен – Н°/R, а отрезок, отсекаемый на оси ординат, равен S°/R. Полученное уравнение называется изобарой химической реакции. На основании изобары химики, как правило, и определяют термодинамические параметры процессов. Уравнение (1.139) справедливо при условии, если энтальпия и энтропия реакции практически не зависят от температуры, а также, если в реакции отсутствуют фазовые переходы. Для определения К_р при некоторой температуре достаточно использовать значения констант равновесия при двух других температурах, которые служат для составления системы уравнений с двумя неизвестными Н° и S°. В уравнение изохоры реакции по аналогии с (1.139) вместо –Н°/RT входит –U°/RT.

Если реакция экзотермическая (Н, увеличение температуры приводит по (1.139) к уменьшению константы равновесия. Это равносильно например по (1.131) смещению равновесия реакции в сторону исходных веществ, что согласуется с принципом Ле Шателье.