Физ химия курс лекций. Лекция 1 Тема Химическая термодинамика
 Скачать 2.63 Mb. Скачать 2.63 Mb.
|
|
ЛЕКЦИЯ 1 Тема 1. Химическая термодинамика Для понимания химических явлений очень важны такие количественные характеристики как температура, внутренняя энергия, работа и теплота. Все эти характеристики, а также связи между ними и взаимные переходы между различными формами энергии рассматриваются в химической термодинамике. В дальнейшем для краткости будем использовать вместо слов «химическая термодинамика» одно слова «термодинамика». Под этим словом следует понимать силу теплоты или что-то, относящееся к силе теплоты. В физической химии термодинамика дает точные соотношения между измеряемыми свойствами систем и отвечает на вопрос, насколько глубоко пройдет данная реакция, прежде чем будет достигнуто равновесие. Она позволяет уверенно предсказать влияние температуры, давления и концентрации на химические равновесия, и рассматривает только начальные и конечные состояния. Так как термодинамика основана на трех законах природы, сформулированных без ссылок на структуру атомов и молекул или механизм химических превращений, то ее выводы обладают общностью и не зависят от статистической теории как классической, так и квантовой. В этом состоит одновременно сила и слабость, преимущество и ограниченность термодинамики. Следует отметить, что классические формулы, связывающие термодинамические величины, применимы и в статистической механике. С другой стороны, статистическая механика позволяет понять внутреннюю сущность термодинамики, но ею трудно пользоваться в случае жидкостей и сильно взаимодействующих систем. 1.1. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ Первый закон термодинамики выражает идею сохранения энергии, которая вначале возникла в механике, а затем распространилась на электростатику и электродинамику. Опыты Джоуля в 1840-1845 гг показали, как можно включить теплоту в закон сохранения энергии. Первый закон термодинамики вводит понятие о внутренней энергии и дает важные результаты по определению тепловых эффектов химических реакций. 1.1.1. Система, окружающая среда, состояние системы и парам3етры состояния Законы термодинамики применяются к системам, представляющим физико-химический интерес. Формально система определяется как некоторая часть объективного мира (или материальной Вселенной), отделенная от окружающей среды замкнутой поверхностью – границей. Практически систему можно описать проще, сказав, например, что она состоит из одного литра водного раствора хлорида натрия некоторой концентрации, находящегося в закрытом сосуде Дьюара при атмосферном давлении и температуре 20 оС. Если граница системы (в нашем примере стенки сосуда) исключает любые взаимодействия с окружающей средой, то система называется изолированной. Если через границу может переходить вещество, то система называется открытой, если вещество через границу не может переходить, то система называется закрытой. Теплота может поступать в закрытую систему или выделяться из нее. Система может претерпевать изменения, при которых она обменивается теплотой и работой с окружающей средой. При этом изменяется как система, так и окружающая среда. Если через границу системы не может проходить теплота, то она называется адиабатической оболочкой, а процессы, происходящие в системе, называются адиабатическими. В этом случае возможен обмен работой с окружающей средой. Про равновесную при данных условиях систему говорят, что она находится в некотором определенном состоянии. В этом случае каждое ее свойство имеет конкретное численное значение. Установлено, что для данного количества газа или жидкости состояние полностью определяется любыми двумя переменными из трех (давление, объем, температура). Такие переменные называются параметрами состояния. Системы бывают гомогенными, если их свойства всюду одинаковые, и гетерогенными, если они состоят из двух или большего числа физически различных и механически разделимых гомогенных частей, называемых фазами. Последним можно дать следующее определение. Фаза – это совокупность частей сложной физико-химической системы, обладающих одинаковыми физическими и химическими свойствами. Например, вода с кусками льда в закрытом сосуде будет представлять собой закрытую систему I (рис.1.1). 3 1 2  Рис. 1.1. Закрытая система I, состоящая из двух фаз: 1 – лед, 2 – вода, 3 – крышка сосуда В ней две фазы: вода и лед. Их химические свойства одинаковы, но физические свойства различны. Система I при p=1атм может существовать только при 0 оС (или 273,15 K). Этой системе можно сообщить некоторое количество теплоты так, чтобы лед расплавился. Процесс превращения одной фазы в другую называется фазовым переходом. При этом лед будет поглощать теплоту, превращаясь в воду при постоянной температуре 273,15 K, которая называется температурой плавления. Для превращения одного моля кристаллического вещества в жидкость при температуре плавления необходимо сообщить ему некоторое количество теплоты, называемое теплотой плавления ( 1.1.2. Работа В термодинамике теплота и работа представляют собой алгебраические величины, которые могут быть положительными или отрицательными. Сила, ускорение и длина пути – величины векторные, они имеют как численные значения, так и направления. Известны следующие выражения силы и работы: F=ma, w=F·l , (1.1) где F – сила, сообщающая массе m ускорение a, w – работа (скалярная величина, характеризуемая только численным значением), l – длина пути, а точкой в (1.1) обозначено скалярное произведение (т.е. произведение численного значения одного вектора и проекции другого вектора на направление первого вектора). Если между направлением силы с численным значением F и длиной с численным значением lимеется угол θ, то вместо (1.1) работа может быть дана следующим выражением: w = F l cosθ . В системе СИ единицей работы является джоуль: 1Дж = 1Н×1м (Н – ньютон, м – метр). Работу можно представить как произведение двух факторов: фактора интенсивности и фактора емкости. Некоторые примеры различных видов работы даны в таблице 1.1. Бесконечно малое количество работы dw, совершаемое силой F на пути dl, равно Fdl. Поскольку давление p – это сила, приходящаяся на единицу площади (p=F/S), то сила, действующая на поршень цилиндра с газом, равна pS, где S – площадь, перпендикулярная направлению движения поршня. Бесконечно малое количество работы, совершаемое в этом случае расширяющимся газом, который сдвигает поршень на расстояние dl, равно pSdl, но Sdl=dV, где dV – приращение объема газа, следовательно, бесконечно малое количество работы равно pdV: dw = p dV. (1.2) Иногда бывает необходимо измерять работу подъема груза. Чтобы поднять массу m в поле земного тяготения, которое сообщает грузу ускорение g, необходимо совершить работу mgh, где h – высота поднятия груза: w = mgh. (1.3) Так как работа алгебраическая величина, то необходимо условиться о ее знаке. Будем принимать для w положительное значение при условии, когда внешняя сила совершает работу над системой. Отрицательное значение w будет иметь при совершении системой работы над окружающей средой. Например, при расширении газа в цилиндре за счет давления газа на поршень. Необходимо отметить, что в некоторых учебниках для w используются обратные знаки. Условимся также о том, что в данном курсе термодинамики, если это специально не оговаривается, то речь будет в основном идти о первых двух видах работы из табл.1.1. Таблица 1.1 Факторы интенсивности и емкости для разных видов работы
1.1.3. Опыты Джоуля, внутренняя энергия и теплота Английский физик Д. Джоуль в середине 19 века показал, что в адиабатических условиях данное количество работы всегда нагревает воду в калориметре на определенное количество градусов, независимо от того, затрачивалась ли эта работа на вращение мешалки с лопастями или на прохождение электрического тока через сопротивление (нагреватель), или на трение твердых тел. Схема двух опытов Джоуля представлена на рис.1.2. Если потянуть конец веревки от точки А до точки В в опыте (а) с силой F, то колесо будет раскручиваться и вращать винт с лопастями. При этом совершится работа, значение которой можно вычислить: w=Fl, (1.4) и которая перейдет в теплоту (q) сосуда с водой вследствие трения лопастей и воды: q=CΔT и q=w, где C - теплоемкость калориметра, показывающая, какое количество теплоты поглощает калориметр при повышении его температуры на один градус; (ΔT=T2 – T1) – прирост температуры калориметра (символ Δ обозначает разность значений данной величины в конечном (T2) и начальном (T1) состояниях). В опыте (в) работу электрического тока также можно вычислить: w=IτE , (1.5) где I – ток в амперах, прошедший по цепи за время τ в секундах, E – разность потенциалов в вольтах, которая прикладывается к нагревателю.     А B F А B F        3 3  6 5 6 5    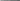   2 4 2 4   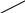 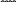  1 7 6 1 7 6 Рис. 1.2. Схема: 1 – калориметр, 2 – лопастной винт, 3 – колесо винта с накрученной веревкой, 4 – источник постоянного напряжения, 5 – реостат, 6 – выключатель, 7 – нагревательный элемент При равенстве значений w по (1.4) и (1.5) вода в калориметре нагреется на одно и то же число градусов. Поскольку данное изменение состояния воды в калориметре может быть достигнуто разными способами, включающими одно и то же количество работы, или при разной последовательности операций (например, выполнение опытов (а) и (в) частями с разными по времени интервалами), оно не зависит от пути процесса, а зависит только от общего количества работы. Свойство системы, изменение которого рассчитывается таким способом, называется внутренней энергией – U. Поскольку внутреннюю энергию системы можно увеличить, совершая над системой работу, то прирост внутренней энергии ΔU приравнивается к работе w, совершенной над системой для перевода ее из одного состояния в другое в адиабатическом процессе: ΔU=w, (1.6) где ΔU=U2 – U1 . (1.7) Равенство (1.6) выполнится и в том случае, если система в адиабатических условиях будет совершать работу над окружающей средой. При этом величины w и ΔU будут отрицательными. Изменение состояния по (1.7) системы может быть достигнуто не только работой в адиабатических условиях, но и другими способами. Например, изменение, эквивалентное достигнутому в опыте (а), можно получить, погружая нагретое тело в воду калориметра. При этом теплота переходит от так называемого теплового источника (нагретого тела) к воде. Однако не говорят, что в воде после этого содержится больше «теплоты» (также в опыте (а) не говорят, что в воде содержится больше «работы»). В результате этого опыта повышается температура воды и ее внутренняя энергия U. Поскольку одно и то же изменение состояния (определяемое измерением таких свойств системы как температура, давление и объем) можно получить, совершая над системой работу или сообщая ей теплоту, то количество теплоты q может быть выражено в механических единицах. Д. Джоуль в своих опытах установил механический эквивалент теплоты, который в настоящее время можно сформулировать следующим образом: затрата 4,184 Дж механической работы над системой производит такое же изменение состояния, как и 1 калория теплоты, полученная системой извне. Напомним, что внесистемная единица измерения теплоты калория – это количество теплоты, которое требуется для нагревания 1 г воды на 1 оС от 14,5 оС до 15,5 оС. Так как теплота - алгебраическая величина, то важно условиться о ее знаках. Будем принимать для q положительное значение, когда система поглощает теплоту из окружающей среды, а отрицательное значение q будет указывать на то, что система отдает теплоту окружающей среде. Если переход теплоты q к системе не сопровождается совершением работы, то вызванное этим переходом изменение внутренней энергии можно выразить следующим равенством: ΔU=q (работа не совершается) . (1.8) Таким образом, теплота, поглощенная закрытой системой в процессе, при котором не совершается работа, равна приросту внутренней энергии системы. Это же можно выразить по-другому: если работа не совершается, то выделившаяся теплота равна убыли внутренней энергии системы. Экспериментально установлено, что если тело А находится в тепловом равновесии с телом С и тело В находиться в тепловом равновесии с телом С, то тела А и В находятся в тепловом равновесии друг с другом. При этом между А, В и С не будет теплообмена. Этот эмпирический факт назвали нулевым законом термодинамики. Нулевой закон термодинамики можно сформулировать также следующим образом: если две системы находятся в тепловом равновесии, то их температура одинакова; если они не находятся в тепловом равновесии, то их температуры различны. 1.1.4. Первый закон термодинамики В природе существует несколько всеобщих законов сохранения. Один из них – закон сохранения энергии. Он показывает, что энергия в изолированной системе сохраняется и может переходить из одной формы в другую в эквивалентных количествах. Энергия – это способность производить работу или переносить теплоту. Известны две формы энергии – потенциальная и кинетическая. Видов энергии много: теплота – это кинетическая энергия структурных частиц веществ; свет – это энергия электромагнитного излучения; химическая энергия – это потенциальная энергия, возникающая вследствие различного расположения атомов и молекул относительно друг друга в различных веществах. На рис.1.3 показаны примеры действия закона сохранения энергии. Сжимая пружину (I), мы совершаем работу, которая переходит в потенциальную – упругую энергию пружины (II). Отдавая потом эту энергию, пружина может совершить работу в виде поднятия груза m на некоторую высоту (III). Точно так же будет выглядеть процесс сжатия газа. Сжимая газ, мы увеличиваем его упругую (потенциальную) энергию, которая затем может быть использована для подъема груза m. При этом будет совершаться менее очевидный процесс – сжатие поршнем атмосферы, окружающей цилиндр. Поэтому часть упругой энергии газа будет передана атмосфере. 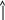   б F б б F б    F m F m       а m а m   а а    I II III I II III Рис. 1.3. Иллюстрация закона сохранения энергии: а – стопор, б - направление движения груза m Рассмотрим далее изолированную систему из двух тел: А – воды и В – железной плиты (рис.1.4). Допустим, что мы ставим А на горячую плиту В. Сразу же теплота от В начнет переходить к А. Когда температуры В и А станут одинаковыми (Т3), теплообмен между ними прекратится. Они окажутся в тепловом равновесии. Так как (А+В) – изолированная система, то по закону сохранения энергии количество теплоты, которое получила при нагревании вода, должно равняться тому количеству теплоты, которое отдала плита: q(H2O) = – q(Fe); (1.9) при этом T2>T3>T1 .  Т1 А Т3 В Т2 Рис.1.4. Схема теплообмена между В и А в изолированной системе (А+В) В этих уравнениях В опыте с изолированной системой (А+В) горячая плита В нагрела воду А, при этом внутренняя энергия А увеличилась, а В – уменьшилось, поэтому вместо равенства (1.9) можно написать выражение (1.14): ΔU(A) = q(H2O), где q(H2O)>0; (1.12) ΔU(B) = q(Fe), где q(Fe)<0; (1.13) ΔU(A+B) = ΔU(A) + ΔU(B) = 0, откуда: ΔU(A) = – ΔU(B). (1.14) 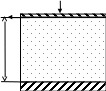 р р  р S h2 пар Т3     A вода T1 h1    B T2 B T2I II Рис.1.5. Схема теплообмена между В и А в адиабатических условиях: I - начало теплообмена; II – тепловое равновесие при Т3=373,15К (Т2 >Т3 ; Т1=Т3) Рассмотрим далее адиабатическую систему (А+В) рис.1.5. Допустим, что закрытая система А в начале процесса (I) состоит из цилиндра с водой, сверху которой имеется невесомый поршень, перемещающийся без трения. Площадь поршня равна S. При контакте А с более нагретой системой В (металлическая плита) теплота от В будет переходить к А. В результате вода будет переходить в парообразное состояние при Т1=373,15 К. Все параметры систем А и В (размеры, масса, Т2) подобраны так, чтобы в конце процесса парообразования конечная температура А и В (Т3) осталась равной Т1(II). Для рассматриваемого случая мы можем повторить формулу (1.9): q(H2O) = – q(Fe); а вот можем ли мы написать для этого случая формулу (1.12)? Оказывается, не можем, так как при переходе воды в пар исходный объем A, равный h1S (V1) увеличивается, и поршень, двигаясь вверх, совершает работу, преодолевая атмосферное давление: p=F/S, (1.15) где F – сила, действующая на поршень, которую можно выразить следующим образом: F = pS. (1.16) Сила F против атмосферного давления действует на расстоянии h2-h1. Их произведение даст работу, совершаемую паром: w = pS(h2 – h1) = p(V2 – V1) = pΔV, (1.17) где Sh2 – объем пара в равновесии II. Так как система А совершает работу (1.17), то ее внутренняя энергия уменьшается на эту величину. И правильно будет вместо (1.12) написать: ΔU(A) = q(H2O) – pΔV (1.18) или ΔU(A) = q(H2O) – w. (1.19) Работа системы А против атмосферного давления идет на увеличение упругой энергии атмосферы (по аналогии с опытом рис.1.3). Если цилиндр с паром (А) поставить на холодную плиту (В), то произойдет обратный процесс – конденсация пара, атмосфера расширится на ΔV и отдаст энергию pΔV сжимаемой системе (А). Формулу (1.9) для различных процессов можно записать в общем виде: ∆U = q + w, (1.20) где все величины могут иметь различные знаки – положительные и отрицательные в зависимости от того, какой процесс происходит с системой. Формула (1.20) – это математическая запись первого закона термодинамики, который подчеркивает, что внутренняя энергия системы может изменяться – убывать или возрастать за счет отдачи или приобретения теплоты и совершения системой или над системой работы. Это различные проявления закона сохранения энергии. Первый закон термодинамики иногда формулируюттак: энергию можно превратить из одной формы в другую, но ее нельзя создать или уничтожить, и общее количество энергии в изолированной системе постоянно. Формула (1.20) выведена при рассмотрении частного случая. Можно показать ее вывод в общем случае, опираясь на формулы (1.6) и (1.8). Для этого рассмотрим переход закрытой системы из состояния (1) в состояние (2), сопровождающийся совершением системой работы (или над ней) в ходе которого система, приведенная в контакт с тепловым источником, приобретает (или теряет) теплоту. Применяя уравнение (1.6) к системе и тепловому источнику, получим: (U2 – U1) + (U2' – U1') = w1, (1.21) где (U2 – U1) – изменение внутренней энергии системы, а (U2' – U1') – изменение внутренней энергии теплового источника. Второе слагаемое левой части уравнения (1.21) равно теплоте, отданной тепловым источником: (U2' – U1')= – q. Тогда уравнение (1.21) приобретает вид: U2 – U1 = ∆U = w+q , (1.22) Видно, что мы получили выражение первого закона термодинамики. Следует подчеркнуть, что этот закон позволяет определить только изменение внутренней энергии, но не абсолютную ее величину. О внутренней энергии в настоящее время можно сказать следующее: все вещества только потому что существуют обладают энергией. Эта энергия складывается из энергии взаимодействий между собой атомов, молекул и ионов, то есть из энергии химических связей, а также из энергии их теплового движения. Сколько этой энергии в веществе мы не знаем. Но чем больше вещества, тем больше энергии. Эту энергию назвали внутренней энергией. Другие формы энергии, как, например, ядерная энергия, в химических системах чаще всего не учитываются и в значение их внутренней энергии не входят. Кроме того, при термодинамическом рассмотрении систем предполагается, что они находятся в состоянии относительного покоя (Екин(системы) = 0), а воздействие на них внешних полей (гравитационного, электрического, магнитного) пренебрежимо мало (Епот(системы) = 0). Тогда полная энергия каждой системы определяется запасом ее внутренней энергии (Еполн = U). Как мы видели, в термодинамике определение U иное – без использования представлений о структурных частицах и строении вещества. Если величина ∆U отрицательна, то можно сказать, что система теряет энергию и что эта энергия выделяется в виде теплоты или работы, совершаемой системой. Первый закон ничего не говорит о том, сколько именно теплоты выделилось, и какое количество работы совершено. Должно только выполняться уравнение (1.22). Он применим в равной мере к тем случаям, когда поглощение теплоты вызывает повышение температуры системы (например, когда кристалл поглощает теплоту при нагревании ниже температуры плавления), так и к тем случаям, когда температура остается постоянной (например, при нагревании кристалла в точке плавления). ЛЕКЦИЯ 2 1.1.5. Энтальпия Представим уравнение (1.20) для некоторой системы, получающей некоторое количество теплоты q и расширяющейся при постоянном давлении, в следующем виде: U2 – U1 = q – p(V2 – V1) , (1.23) где U1, V1 – начальные параметры системы, U2, V2 – конечные параметры системы. Из уравнения (1.23) можно получить выражение для вычисления q: q = (U2 + pV2) – (U1 + pV1) , (1.24) Обозначим далее начальные и конечные параметры в скобках соответственно через H1 и H2. Тогда поглощенная системой теплота представит разность двух величин: q = H2 – H1 = ΔН. (1.25) В результате перехода от H1 к H2 система приняла количество тепла q, то есть теплосодержание системы возросло. Поэтому величину H назвали теплосодержанием. Ее значение по (1.24) следующее: H = U + pV. (1.26) Так как по (1.26) H содержит в себе внутреннюю энергию U, то абсолютную величину H нельзя определить (как и U). Однако изменение H в любой системе можно определить по (1.25). Величину H назвали также греческим словом энтальпия (от греческого «энтальпо» – нагреваю). Ей можно дать следующее определение: теплота, поглощенная в процессе, протекающем при постоянном давлении, равна изменению энтальпии, если единственным видом произведенной работы является работа расширения системы. Энтальпия является функцией состояния системы (так же, как р, V, U, T), то есть она зависит только от начального и конечного состояния системы и не зависит от пути перехода между этими состояниями, ее размерность – размерность энергии (единицей измерения в СИ является джоуль). Дифференцируя (1.26), получим: dH = dU + d(pV), (1.27) dH = dU + Vdp + pdV, так как при p=const dp=0, то dH = dU + pdV, (1.28) или в интегральной форме: ΔH = ΔU + p ΔV. (1.29) Изменение энтальпии системы – это изменение ее внутренней энергии при постоянном давлении (чаще всего при атмосферном) с учетом работы ее расширения и сжатия. |
