Физ химия курс лекций. Лекция 1 Тема Химическая термодинамика

• Название: Лекция 1 Тема Химическая термодинамика
• Дата: 30.04.2023
• Размер: 2.63 Mb.
• Имя файла: Физ химия курс лекций.doc
• Тип: Лекция; #1098252
• страница: 5 из 15

1.3.3. Выражение второго закона термодинамики через энтропию

Второй закон термодинамики рассматривают как постулат, о справедливости которого следует судить по результатам его применения. Они таковы – второй закон термодинамики справедлив для макроскопических систем, так как известно, что всегда выполняются все соотношения, выведенные из этого закона.

Имеются различные формулировки второго закона, которые звучат по-разному, но приводят к одним и тем же результатам. Английский физик У.Томсон (получивший за научные заслуги почетный титул лорда Кельвина) в 1851 году сформулировал второй закон следующим образом: невозможно использовать циклический процесс (ряд последовательных операций, которые возвращают систему в исходное состояние) для превращения в работу теплоты, взятой из теплового источника без одновременного переноса некоторого количества теплоты от более горячего тела к более холодному. Немецкий физик Р.Ю.Э. Клаузиус в 1850 году дал первую формулировку второго закона термодинамики в таком виде: невозможно использовать циклический процесс для переноса теплоты от более холодного тела к более горячему без одновременного превращения некоторого количества работы в теплоту. Из этих формулировок видно, что исторически развитие представлений о втором законе термодинамики было тесно связано с изучением тепловых машин. Так как такой подход далек от химии, то его надо было рассмотреть с использованием величин, которые можно непосредственно применить к химическим реакциям. Этот подход предложен в 1882 году немецким ученым Г.Л.Ф. Гельмгольцем и развит в дальнейшем американским физиком-теоретиком Д.У.Гиббсом. Он включал в себя понятие энтропии S.

Второй закон химической термодинамики можно сформулировать следующим образом: для любого бесконечно малого процесса дифференциал энтропии dS больше, чем dq/T или равен этой величине:

dS≥dq/T . (1.78)

Этим второй закон устанавливает различие между двумя типами изменений: изменения, для которых дифференциал энтропии больше dq/T (1.79), являются необратимыми (самопроизвольными), а изменения, для которых дифференциал энтропии равен dq/T (1.80), являются обратимыми:

dS>dq/T, (1.79)

dS = dq/T . (1.80)

К обратимым изменениям относится, например, перенос бесконечно малого количества теплоты от теплового резервуара с температурой T к резервуару, температура которого ниже на бесконечно малую величину (как, например, в процессе по рис. 1.12), или превращение бесконечно малого количества исходного вещества в продукт реакции в равновесной реакционной смеси.

На основании утверждения, что для необратимого процесса dS>dq/T, второй закон термодинамики дает критерий, позволяющий судить о возможности протекания химической реакции или физико-химического процесса. Только показав, что выполняется (1.79), можно утверждать, что этот процесс или реакция произойдут самопроизвольно.

Уравнение (1.78) удобно применять к изолированным системам с постоянной внутренней энергией U и постоянным объемом V, которые не обмениваются с окружающей средой ни теплотой, ни работой, ни веществом. Для таких систем dq=0, и уравнения (1.79), (1.80) приобретают следующий вид:

dS>0, (1.81)

в случае бесконечно малого необратимого изменения, и

dS = 0, (1.82)

в случае бесконечно малого обратимого изменения. Для конечного необратимого процесса в изолированной системе

∆S > 0, (1.83)

а для конечного обратимого процесса

∆S = 0. (1.84)

Таким образом, когда в изолированной системе происходит необратимое изменение, энтропия возрастает. Когда все возможности увеличения энтропии при самопроизвольных процессах будут исчерпаны, ее значение будет максимальным.

1.3.4. Расчет изменений энтропии для обратимых процессов

Три типа процессов, которые можно осуществить обратимо, включают: фазовые переходы (например, испарение жидкости с образованием насыщенного пара, кристаллизация или плавление при T_пл), нагревание вещества и расширение идеального газа. Для них легко рассчитать изменение энтропии. Например, в случае фазовых переходов, протекающих при постоянной температуре, интегрирование (1.77) дает:

S₂ – S₁ = ∆S = q_обр/T,

где q_обр – теплота, поглощенная при обратимом изменении.

Для одного моля вещества при постоянных температуре и давлении вместо (1.77) получим:

(1.85)

Это уравнение можно использовать также для расчета энтропии возгонки или в случае изменения энтропии при переходе одной формы вещества в другую. Поскольку количество теплоты, полученной системой, равно количеству теплоты, отданному окружающей средой, то изменение энтропии окружающей среды равно изменению энтропии системы с обратным знаком. Суммарное изменение же энтропии для системы и окружающей среды равно нулю, если перенос теплоты происходит обратимо, как и требует уравнение (1.82).

Рассмотрим в качестве примера кипение н-гексана при 68,7 ^оС. При этой температуре теплота испарения н-гексана при атмосферном давлении равна 28,85∙10³ Дж/моль. Если при этих условиях жидкость испаряется с образованием насыщенного пара, то процесс обратим, и изменение ее энтропии в расчете на один моль определяется уравнением (1.85):



Мольная энтропия пара всегда больше, чем энтропия жидкости, с которой пар находится в равновесии, а мольная энтропия жидкости (учитывая (1.85)) всегда больше, чем энтропия твердого вещества в точке плавления. Действительно, согласно представлению об энтропии как о мере неупорядоченности системы, молекулы газа располагаются в пространства более беспорядочно, чем молекулы жидкости, а молекулы жидкости более неупорядочены, чем молекулы твердого тела:

(1.86)

Возрастание энтропии системы, вызванное увеличением температуры, можно рассчитать, так как изменение температуры можно осуществить обратимо. Если нагревание проводить при постоянном давлении, то теплота, поглощенная на каждой бесконечно малой стадии равна теплоемкости С_р, умноженной на бесконечно малый прирост температуры dT и, следовательно:

dS = C_р dT/T. (1.87)

Интегрирование уравнения (1.87) в пределах от T₁ до Т₂ дает: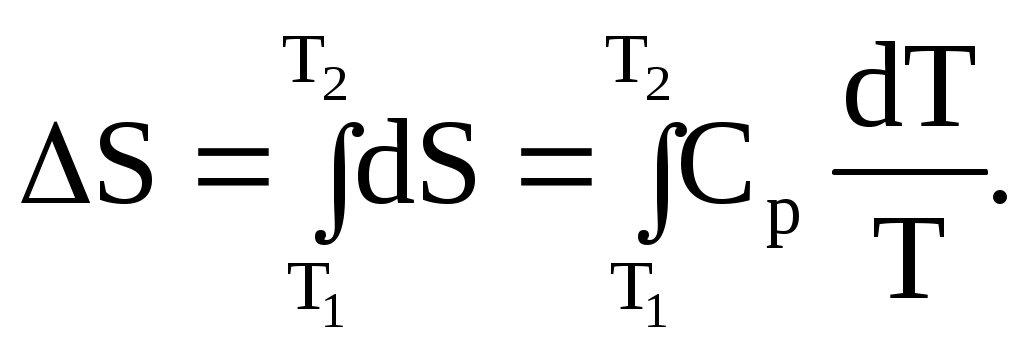

(1.88)

Если C_p не зависит от температуры, то вместо (1.88) следует написать: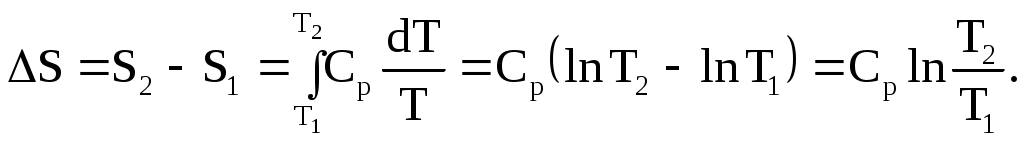

(1.89)

Факт возрастания энтропии с ростом температуры согласуется с большей неупорядоченностью движения молекул при более высокой температуре. Если нагревание проводить при постоянном объеме, то вместо С_р используют C_v.

Рассмотрим далее, как изменяется энтропия идеального газа при обратимом увеличении температуры и объема. Для этого надо сообщать газу бесконечно малыми порциями теплоту dq. Тогда, в соответствии с первым законом термодинамики, для одного моля газа можно написать следующее уравнение:

(1.90)

Так как газ идеальный, то p = RT/V, и вместо (1.90) будет:

(1.91)

Бесконечно малое изменение энтропии в расчете на один моль газа, сопровождающее бесконечно малые изменения температуры dT и объема будет, следующим:

(1.92)

Предполагая независимость С_v от температуры и объема после интегрирования, получим:

(1.93)

Это уравнение применимо к любому изменению (обратимому и необратимому) состояния идеального газа, потому что ∆S зависит только от значения энтропии в начальном и конечном состояниях. Если температура поддерживается постоянной, то вместо (1.93) получим:

(1.94)

Например, для десятикратного увеличения объема идеального газа по (1.94):

= 8,314∙2,303 = 19,2 Дж/К∙моль.

1.3.5. Расчет изменений энтропии для необратимых процессов

Изменение энтропии для необратимого процесса можно рассчитать, рассматривая путь, по которому этот процесс может быть осуществлен в несколько стадий. Рассмотрим это на примере замерзания переохлажденной воды при температуре ниже ее точки замерзания.

Замерзание моля переохлажденной воды при 263К является необратимым процессом, но его можно провести в следующие три обратимые стадии, для которых указаны изменения энтропии:

1.

2.

3.

Для кристаллизации воды при 273К q_{крист., обр.} = -333,46 Дж/г. Удельную теплоемкость в этом диапазоне температур можно принять равной 4,184 Дж/(г∙К) для воды и 2,05 Дж/(г∙К) для льда. Тогда общее изменение энтропии воды в результате перехода одного моля жидкой воды при 263К в лед получится простым суммированием приведенных трех изменений энтропии:

∆S = (18г/моль)[4,184Дж/(г·К)](2,303)lg273/263 + +(18г/моль)(–333,46Дж/г)/273К+(18г/моль)[2,05Дж/(К·г)](2,303)lg273/263= = – 20,58 Дж/(моль·К).

Уменьшение энтропии соответствует увеличению структурной упорядоченности при замерзании воды.

Чтобы показать, что энтропия изолированной системы возрастает, если в ней происходит самопроизвольный процесс, рассмотрим переохлажденную воду при 263К, находящуюся в контакте с большим тепловым резервуаром при такой же температуре. При замерзании воды изменение энтропии изолированной системы включает как изменение энтропии воды, так и изменение энтропии резервуара. Если тепловой резервуар велик, то теплота, выделенная при замерзании воды, поглощается резервуаром, вызывая лишь бесконечно малое повышение температуры. Поскольку теплота кристаллизации воды при 263К равна 312,1Дж/г, то изменение энтропии резервуара в этом обратимом процессе составляет:

ΔS_резерв= (18г/моль)(312,1Дж/г)/263К = 21,34 Дж/(моль·К).

Изменение энтропии системы вода-резервуар составляет:

ΔS_сист= 21,34 – 20,58 = 0,76 Дж/(моль·К).

Таким образом, общая энтропия изолированной системы, включающей воду и резервуар, возрастает, что согласуется с неравенством (1.79).

1.3.6. Энтропия смешения идеальных газов

Если привести в соприкосновение два идеальных газа, находящихся при одинаковых давлении и температуре, то они будут самопроизвольно диффундировать друг в друга, пока газовая фаза не станет макроскопически однородной. Поскольку между молекулами идеальных газов нет взаимодействия, то при их смешении энергия не изменяется. Смешение происходит самопроизвольно только за счет увеличения энтропии. Это изменение энтропии равно изменению, которое произошло бы, если бы каждому газу была предоставлена возможность изотермически расширяться от его начального объема до конечного общего объема смеси. Изменение энтропии каждого газа можно вычислить по уравнению (1.94). Для газа 1 изменение энтропии равно:

ΔS₁=n₁R ln (V₁ + V₂)/V₁ , (1.95)

где n₁ – число молей газа 1 , V₁ – начальный объем газа 1, a V₂ – начальный объем газа 2, так что V₁+V₂ представляет конечный объем смеси газов. Для ∆S₂ выражение будет аналогичное (1.95), а суммарная энтропия расширения этих двух газов будет равна:

ΔS_смеш = n_lRln(V₁ + V₂)/V₁ +n₂ Rln(V₁+V₂)/V₂ , (1.96)

где n₂ – число молей газа 2. Мольные доли Х₁ и Х₂ двух идеальных газов выражаются равенствами:

Х₁ = n₁/(n₁+n₂)=V₁/(V₁+V₂) ,

Х₂ = n₂/(n₁+n₂)=V₂/(V₁+V₂) .

Поэтому вместо (1.96) будет:

∆S_смеш = –R(n₁ ln X₁ + n₂ lnХ₂). (1.97)

Если n₁+n₂=1, то изменение энтропии является мольной величиной,
и уравнение (1.97) можно записать следующим образом:

Δ _смеш = –R(X₁1nХ₁ + Х₂1nХ₂) . (1.98)

Например, можно рассчитать изменение энтропии в результате смешения 1 моля водорода и 1 моля азота при 1 атм и постоянной температуре. Газы считаются идеальными.

∆S_смеш= –2,303 R (n₁ lgX₁ + n₂ lgХ₂) = – (2,303) (8,314) (lg0,5 + lg 0,5) = =11,52 Дж/К.

Энтропия смешения по (1.98) положительна, так как Х₁<1 и Х₂<1.
Следовательно, согласно уравнению (1.98) в изолированной системе
диффузия одного газа в другой происходит самопроизвольно, хотя
энергия системы при этом не уменьшается. Уравнение (1.98) можно
записать в обобщенном виде и для смешения одного моля нескольких
(i) компонентов с образованием идеального раствора:

Δ _смеш = – R ΣX_i lnХ_i . (1.99)

ЛЕКЦИЯ 6 1.3.7. Критерии химического равновесия

Согласно второму закону термодинамики процесс является самопроизвольным, если протекание его в изолированной системе приводит к увеличению энтропии системы. В данном разделе показано, как из этой формулировки можно получить еще более полезные критерии самопроизвольных химических реакций и физико-химических процессов.

В практических целях важно знать, находится ли система в равновесном или только в метастабильном состоянии. Под равновесным состоянием подразумевается такое состояние, в котором система при данных условиях не испытывает самопроизвольных изменений. При этом любое бесконечно малое изменение, которое могло бы произойти в системе, должно быть обратимым, так как любое необратимое изменение привело бы к сдвигу равновесия.

Рассмотрим систему, находящуюся в тепловом контакте с тепловым резервуаром при температуре Т, в которой происходит бесконечно малый необратимый процесс и совершается только работа расширения. Допустим, что система при этом принимает от теплового резервуара количество теплоты dq, и поскольку процесс в ней необратим, то увеличение энтропии для системы > чем dq/T:

dS >dq/T. (1.100)

Из этого неравенства следует, что разность dq – TdS отрицательная:

dq – TdS <0. (1.101)

Так как совершается только работа расширения то dq=dU+pdV. Подставляя это выражение в (1.101), получим:

dU + рdV – TdS < 0. (1.102)

Неравенство (1.102) применимо во всех случаях, когда происходит самопроизвольный процесс и совершается только работа расширения. Проанализируем неравенство (1.102).

I. Допустим, что объем и энтропия системы сохраняются постоянными, тогда:

(dU)_V,S < 0. (1.103)

То есть в этом случае внутренняя энергия системы должна уменьшаться, что согласуется с известным условием, а именно, что стабильным состоянием системы является состояние с наименьшей энергией.

II. Объем и внутреннюю энергию системы можно поддерживать
постоянным, изолировав систему. Тогда уравнение (1.02) переходит в следующее:

dS >0, (1.104)

и, следовательно, энтропия в таком необратимом процессе должна возрастать. Если бы система не была изолированной, то необходимо было бы

также рассматривать изменение энтропии в окружающей среде или смежных системах.

III. Если в ходе бесконечно малого необратимого процесса объем
сохраняется постоянным, то неравенство (1.102) переходит в
следующее неравенство:

(dU – TdS)_V < 0, (1.105)

которое для процессов, протекающих при постоянной температуре можно представить в следующем виде:

d(U – TS)_T,V < 0. (1.106)

Величина в скобках U—TS называется свободной энергией Гельмгольца или изохорным потенциалом и обозначается символом А:

A = U – TS. (1.107)

Из уравнений (1.106) и (1.107) для самопроизвольных процессов можно получить:

(dA)_T,V < 0. (1.108)

Таким образом, в необратимом процессе при постоянных Т и V свободная энергия Гелъмгольца (изохорный потенциал) уменьшается.

IV. Физические процессы и химические реакции чаще всего протекают при постоянных давлении и температуре. В этом случае неравенство (1.102) можно записать в виде:

d(U+рV – TS)_T,р < 0. (1.109)

Величина U+рV–TS называется свободной энергией Гиббса или
изобарным потенциалом и обозначается символом G:

G = U + рV – TS = H – TS . (1.110)

Из уравнений (1.109) и (1.110) получаем:

(dG)_T,p < 0. (1.111)

Таким образом, в необратимых процессах при постоянных Т и р, когда совершается только работа расширения, свободная энергия Гиббса (изобарный потенциал) уменьшается.

Если рассмотренные процессы в I – IV обратимые, то все знаки полученных неравенств нужно заменить знаками равенства в соответствии с уравнением (1.80). Условия обратимости и необратимости процессов, в которых совершается только работа расширения, даны в таблице 1.3.

Таблица 1.3

Критерии необратимости и обратимости процессов, в которых не совершается или совершается только работа расширения

Для необратимых процессов	Для обратимых процессов
(dS)V,U > 0	(dS)V,U = 0
(dU)V,S < 0	(dU)V,S = 0
(dA)T,V < 0	(dA)T,V = 0
(dG) T,p< 0	(dG)T,p = 0

Каждая строка этой таблицы представляет собой математическую формулировку второго закона термодинамики. Поскольку изобарный потенциал уменьшается в необратимых процессах при постоянных Т и р, то он становится минимальным в конечном равновесном состоянии, где dG=0 для любого бесконечно малого изменения. Например, при испарении бесконечно малого количества воды, находящейся в равновесии с насыщенным паром, при постоянных температуре и давлении dG=0.

Соотношения таблицы 1.3 можно применять как к бесконечно малым, так и к конечным изменениям, заменив в последнем случае d на ∆. Однако следует помнить, что самопроизвольные процессы всегда приводят к минимуму (в случае G_Т,р) или к максимуму (как в случае S изолированной системы) функции, а не к какому-то другому ее значению, даже если переход к последнему удовлетворял бы соответствующему неравенству.

Следует подчеркнуть, что приведенные в таблице 1.3 критерии показывают, является ли данный процесс самопроизвольным, но они не дают еще основания считать, что этот процесс будет протекать с заметной скоростью. Например, при стандартных условиях для смеси 1 моля углерода (энергию Гиббса (∆G°) образования наиболее устойчивой модификации простого вещества принимают условно равной нулю) и 1 моля кислорода изобарный потенциал больше чем для одного моля диоксида углерода (0 кДж/моль и –394,4 кДж/моль, соответственно), следовательно, имеется возможность образования диоксида углерода из углерода и кислорода при 1 атм и 298К, однако скорость реакции настолько мала, что углерод в контакте с кислородом при указанных условиях может существовать длительное время. И эта реакция оказывается возможной только теоретически. Обратный процесс – разложение диоксида углерода, сопровождающийся увеличением G, является несамопроизвольным процессом. Он может произойти только при внешнем воздействии.

Приведенные рассуждения ограничивались системами, способными производить только работу расширения. Если бы система содержала гальванический элемент, то могла бы также
совершаться электрическая работа, и критерии равновесия были бы
другими. Поэтому рассмотрим бесконечно малое изменение G в
общем случае. Оно по (1.110) равно:

dG = dU + рdV + Vdр – TdS – SdT. (1.112)

При постоянных температуре и давлении получим:

dG = dU + рdV – TdS. (1.113)

Подставляя в (1.112) dU=dq+dw получаем:

dG = dq + dw + рdV – TdS. (1.114)

Если изменение осуществляется с помощью обратимого процесса, а теплота dq переносится из резервуара, находящегося при той же температуре Т, что и система, то по (1.114) dq=TdS и dw=dw_обр. Для этого случая уравнение (1.112) можно записать в виде:

– dG = – w_oбp – рdV. (1.115)

Таким образом, для обратимого процесса при постоянных температуре и давлении уменьшение изобарного потенциала равно максимальной работе, которая может быть совершена системой помимо работы расширения.

Если изменение осуществляется с помощью необратимого процесса, а теплота dq переносится из резервуара, находящегося при той же температуре Т, что и система, то по (1.79) ТdS >dq . Подстановка последнего неравенства в (1.114) дает:

– dG > – dw_обр – рdV. (1.116)

Для конечного изменения:

– ∆G > – w_обр – р∆V. (1.117)

Таким образом, для необратимого процесса при постоянных температуре и давлении уменьшение изобарного потенциала больше, чем максимальная работа, совершенная системой помимо работы расширения.

Поскольку при постоянном давлении, учитывая уравнение (1.115) и (1.110), ΔG=∆A + р∆V, то из уравнения (1.115) следует, что для процесса при постоянных температуре и давлении выполняется равенство:

– ΔA = – w_обр. (1.118)

Следовательно, уменьшение изохорного потенциала равно максимальному количеству работы, которое может быть произведено системой в изотермическом процессе.