Физ химия курс лекций. Лекция 1 Тема Химическая термодинамика
 Скачать 2.63 Mb.
|
|
1.1.6. Теплоемкость Теплоемкостью системы (С) называется количество теплоты, необходимое для того, чтобы повысить ее температуру на какую-то определенную величину (обычно на один градус). Иными словами, теплоемкость – это отношение поглощенной теплоты к приросту температуры: С = q/ΔT. (1.30) Теплоемкость зависит от температуры, и при данной температуре представляет собой предел, к которому стремится указанное соотношение при уменьшении ΔТ. Внутренняя энергия химически инертной системы с фиксированной массой (закрытая система) является функцией температуры и объема (U=f(T,V)). Поскольку U – функция состояния, то дифференциал ее dU является полным и может быть представлен следующим выражением: dU = (∂U/∂T)VdT + (∂U/∂V)TdV . (1.31) Первый член представляет собой изменение внутренней энергии за счет изменения температуры, второй член – изменение внутренней энергии за счет изменения объема. Поскольку производится лишь работа расширения, то, учитывая (1.25) и (1.28), для поглощенной теплоты можно написать следующее выражение: dq = dU + pdV = (∂U/∂T)VdT + [p + (∂U/∂V)T]dV. (1.32) Второе выражение (1.32) для dq получено подстановкой в первое значения dU из (1.31). Из (1.32) следует, что количество поглощенной теплоты зависит не только от прироста температуры, но и от изменения объема. Если объем системы поддерживается постоянным, то: dqv = (∂U/∂T)VdT. (1.33) Величина dq/dT может быть измерена экспериментально при постоянном объеме и называется теплоемкостью системы при постоянном объеме СV: CV = dqV/dT = (∂U/∂T)V . (1.34) Второе выражение для CV в (1.34) получено из уравнения (1.33). Если рассматривается один моль чистого вещества, то теплоемкость представляет собой мольную величину (или молярную теплоемкость):  (1.35)На основании (1.35) можно вычислять изменения внутренней энергии одного моля вещества в результате нагревания его от Т1 до Т2:  (1.36)Для химически инертной системы с фиксированной массой удобно рассматривать энтальпию H, как функцию температуры и давления. Тогда бесконечно малое изменение энтальпии dH, вызванное изменением температуры dT и давления dp, дается следующим выражением: dH = (∂H/∂T)pdT + (∂H/∂p)Tdр. (1.37) Если давление постоянное, то dH = dqp, и уравнение (1.37) переходит в уравнение (1.38): dqp = (∂H/∂T)pdT. (1.38) Величина dqp/dT называется теплоемкостью при постоянном давлении Ср: Cp = dqр/dT = (∂H/∂T)p . (1.39) Для одного моля чистого вещества:  (1.40)Для вычисления теплоты, поглощаемой при нагревании газа от одной температуры до другой, уравнение (1.40) следует проинтегрировать в нужных пределах, и тогда по аналогии с (1.36) получим:  (1.41)Теплоемкость при постоянном давлении Cp всегда больше, чем теплоемкость при постоянном объеме СV, так как нагревание вещества при постоянном давлении сопровождается работой расширения. Уравнение для разности Cp – CV можно вывести, разделив уравнение (1.32) на dT и принимая давление постоянным: dqp/dT = (∂U/∂T)V + [p + (∂U/∂V)T](∂V/∂T)p . (1.42) Учитывая (1.34) и (1.39) для одного моля вещества по (1.42) получим:  (1.43)Величину (∂U/∂V)T можно измерить экспериментально. Поскольку для идеального газа выполняется: dU = (∂U/∂V)T dV= 0, (1.44) то в соответствии с уравнением состояния идеального газа: (∂V/∂T)p = R/p уравнение (1.43) приобретает вид:  (1.45)Это соотношение для идеального газа можно представить себе достаточно наглядно. Действительно, когда моль идеального газа в цилиндре нагревается при постоянном давлении, то производится работа перемещения поршня, равная  . Если температура изменяется на 1К, то совершенная работа равна R. Это и есть величина, на которую энергия, требуемая для нагревания одного моля идеального газа на 1К при постоянном давлении, превышает энергию, необходимую для такого же нагревания при постоянном объеме.Общее выражение для  в случае любых газов выводится с использованием второго закона термодинамики. Не давая вывода, приведем его результат: (1.46)где α – коэффициент изобарического расширения газа, равный (∂V/∂T)p/V, k – коэффициент сжимаемости газа, равный - (∂V/∂p)T/V. Следует отметить, что чем сложнее молекулы газа, тем больше его мольная теплоемкость, и тем большее влияние на ее значение оказывает температура. Укажем также на некоторые особенности теплоемкости твердых тел. Простейшим типом твердого тела является кристалл химического элемента, в котором каждый узел решетки занятатомом. В классической механике принято и доказано, что каждый атом ведет себя как простой гармонический осциллятор с тремя степенями свободы (по направлениям осей х, у и z). Тогда:  (1.47)где R — вклад, вносимый каждой степенью свободы. Этому равенству приблизительно удовлетворяет значение  при комнатнойтемпературе для всех элементов тяжелее калия. На этом основан закон Дюлонга и Пти: при комнатной температуре произведение удельной теплоемкости при постоянном давлении (Суд;Дж/(г К)) и молярной массы элемента (М; г/моль), находящегося в твердом состоянии, есть постоянная величина  , равная примерно 26,8 Дж/(К моль): (1.48)Однако элементы, расположенные в начале периодической системы Д.И.Менделеева, имеют в твердом состоянии более низкие значения теплоемкости, чем по (1.48). И кроме этого, для всех твердых веществ теплоемкости стремятся к нулю по мере приближения температуры к абсолютному нулю. Эти явления нельзя было объяснить в рамках классической физики. Они получили свое объяснение только в квантовой механике. Приблизительную теорию разработал в 1911 г. А. Эйнштейн. Более точная теория была разработана Дебаем. Он показал, что при достаточно низких температурах теплоемкость пропорциональна абсолютной температуре в третьей степени:  (1.49)где θ- характеристическая температура по Дебаю, значения которой для разных атомных кристаллов различны. Установлено, что при увеличении температуры в некоторых пределах теплоемкость большинства веществ растет. Теплота при этом расходуется на увеличение скорости поступательного, вращательного и колебательного движений атомов и молекул. Теплоемкость веществ при разных температурах определяют опытным путем или вычисляют теоретически. Экспериментальные значения Ср при разных Т можно представить в виде эмпирического уравнения: Cp = a + bT + cT2 + eT3, (1.50) где a, b, c, e - коэффициенты, которые для разных веществ определены эмпирически или на основании молекулярно-статистических расчетов и занесены в таблицы. Чтобы определить среднее значение теплоемкости вещества в некотором интервале температур (от Т1 до Т2), нужно проинтегрировать выражение (1.50) по температуре и разделить полученную величину на интервал температур:  И Ср В А Т1 Т2 Т нтегрирование можно провести графически, если имеется график зависимости теплоемкости вещества от температуры, как, например, рис.1.6:  Рис. 1.6. Температурная зависимость Ср вещества 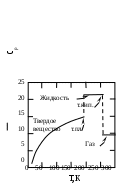 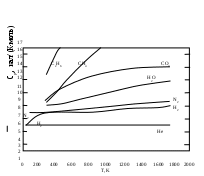 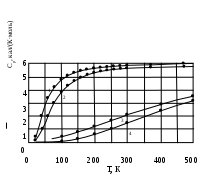 а) б)в) Рис.1.7. Зависимость от температуры мольной теплоемкости при постоянном давлении: а) некоторых газов; б) оксида серы IV в разных агрегатных состояниях; в) некоторых твердых ве- ществ: (1) – серебра, (2) – меди, (3) – графита, (4) – алмаза Для определения средней теплоемкости графическим методом нужно измерить площадь Т1АВТ2 и разделить ее на разность (Т2 – Т1). На рис. 1.7 в качестве примера показана зависимость  от Т для некоторых газов (а), оксида серы IV (б) и твердых веществ (в). Точки разрывов на графике (б) соответствуют фазовым переходам SO2: точке плавления (т. пл.) и точке кипения (т. кип.). 1.2. ТЕРМОХИМИЯ В термохимии рассматриваются вопросы, связанные с теплотой, поглощаемой или выделяемой в химических реакциях, при фазовых превращениях, при растворении веществ или при разбавлении растворов. Если в указанных процессах теплота выделяется, то они называются экзотермическими. В них значения Δ Н и ΔU отрицательны (Δ Н <0, ΔU <0). Если в указанных процессах теплота поглощается, то они называются эндотермическими. В них значения Δ Н и ΔU положительны (Δ Н >0 и ΔU >0). Значения Δ Н и ΔU химических реакций зависят от того, в каком состоянии находятся исходные вещества (реагенты) и продукты реакций. Так, например, теплота сгорания одного моля графита не равна теплоте сгорания одного моля алмаза. Чтобы облегчить табулирование термодинамических данных, приняты определенные стандартные состояния, для которых и приводятся значения термодинамических свойств. Стандартное состояние газа — это идеальный газ при 1атм и данной температуре. Для твердого вещества — это характерное (наиболее устойчивое) кристаллическое состояние при 1 атм и данной температуре, например, графит для углерода и ромбическая сера для серы. Стандартное состояние растворенного вещества — это концентрация, при которой активность равна единице. Температуру стандартного состояния указывают подстрочным индексом (например, ΔН298). Термодинамические функции часто табулируются при 298К, но следует помнить, что стандартное состояние не обязательно подразумевает эту температуру. Если реагенты в стандартных состояниях превращаются в продукты также в стандартных состояниях, то их термодинамические величины и изменения термодинамических величин помечаются надстрочным индексом «0» (например, Н0298). Агрегатное состояние веществ в термодинамике указывается в скобках после обозначения вещества следующим образом: газообразное — (г), кристаллическое – (к), жидкое — (ж), твердое – (тв), растворенное в воде – (водн). 1.2.1. Калориметрические измерения Экспериментальные результаты в термохимии получают при помощи приборов, которые называются калориметрами и калориметрическими бомбами. На рис.1.8 показаны схемы двух типов калориметров: (а) – калориметр, измеряющий тепловые эффекты реакций, протекающих при постоянном объеме в камере для химических реакций (Х.р.); б – калориметр с переменным объемом камеры (Х.р.), которая через поршень адиабатически соединяется с атмосферой, что обусловливает в ней постоянное значение давления, равное атмосферному. При калориметрических измерениях термометром фиксируется изменение температуры воды и самого калориметра (∆T = T2 – T1), происходящее вследствие выделения или поглощения теплоты в результате протекания реакции или фазового перехода в камере для химических реакций. Так как известна теплоемкость калориметра С, то, зная ∆T, можно вычислить количество теплоты, полученное калориметром от процесса, происходящего в его камере: q = C∆T. 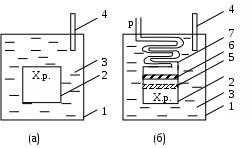 Рис. 1.8. Схемы калориметров: а – при постоянном V и переменном р; б – при постоянном р и переменном V; 1 – металлический корпус калориметра, 2 – камера для химических реакций, 3 – вода, 4 – термометр, 5 – поршень (в конечном положении для реакции (1.51), 6 – поршень (в начальном положении для реакции (1.51), 7 – змеевик, связывающий камеру (Х.р.) с атмосферой Рассмотрим в качестве примера реакцию сгорания оксида углеродаII: СО(г) + 0,5 О2(г) = СО2(г) + qp. (1.51) n 1 моль 0,5 моля 1моль  V 22,4 л 11,2 л 22,4 л при 273,15 К33,6 л По (1.51) видно, что в реакцию вступают 1,5 моля газообразных реагентов, а образуется 1 моль газообразного продукта. Их объемы при 273,15 К составили бы соответственно (V=nVм): 33,6л и 22,4 л. Так как эта реакция является экзотермической, то её тепловой эффект (в данном случае индекс р обозначает – реакции) qp ставится в виде слагаемого в уравнении справа вместе с продуктами. Для эндотермических реакций qp можно ставить в уравнении в виде слагаемого слева вместе с реагентами или вместе с продуктами справа, но с отрицательным знаком. В термохимии уравнения реакций включают их тепловые эффекты и называются термохимическими уравнениями. Если тепловой эффект реакции (1.51) измерить при помощи калориметра (а) (qa=Ca∆Ta), то он будет соответствовать ∆U°p и составит –281,76 кДж. В случае калориметра (б) тепловой эффект (qб=Cб∆Tб) будет соответствовать ∆Hºp и составит –283 кДж. Таким образом, измерения показывают, что тепловой эффект реакции (1.51) в разных калориметрах различен (qа ≠ qб). Покажем, как по (1.29), зная величину ∆Uºp , можно вычислить ∆Hºp (1.51): ∆Hºp = ∆Uºp+ pº∆V, где pº – стандартное давление 1атм, равное в СИ 101325 Н/м2; ∆V – изменение объема реакционной системы при 298 К, равное ∆Vо·298К· 10-3м3/273,15К (множитель 10-3 для перевода ∆Vº в м3, так как ∆Vº = Vº2 – Vº1 = 22,4л – 33,6л = – 11,2л); ∆Hºp=–281,76кДж+101325(Н/м2)·(–11,2·10-3м3·298К/273,15К)·10-3= = – 281,76кДж –1,24 кДж = – 283 кДж Второе слагаемое ∆Hºp представляет собой упругую энергию, которую система (1.51) в калориметре (а) получает от атмосферы, сжимающей систему. Коэффициент 10-3 в этом слагаемом введен для перевода джоулей в килоджоули. Как уже отмечалось ранее, в химии процессы чаще всего проводят при р=1атм и если в таком случае ∆Vp ≈ 0, то тепловой эффект реакции равен ∆Up. Для подобных реакций выполняется соотношение: ∆Up ≈ ∆Hp . Поэтому тепловые эффекты всех реакций и фазовых переходов принято оценивать в виде изменений энтальпии. Поскольку в термохимии наибольшее значение имеют теплоты сгорания, то для получения полного теплового эффекта сгорания вещества процесс его сгорания осуществляют в стальной калориметрической бомбе, содержащей кислород под давлением 25 атм. В таких условиях, например, все углеводороды сгорают полностью, образуя воду и оксид углеродаIV. Так, в частности, определяют числа калорий, получаемых при сгорании различных видов пищи. Однако следует знать, что в диетологии, когда речь идет о питании, под словом «калория» подразумевают килокалорию. ЛЕКЦИЯ 3 1.2.2. Стандартные энтальпии образования и фазовых превращений веществ В термохимии принято считать стандартные энтальпии образования химических элементов и элементарных веществ в наиболее устойчивой форме равными нулю. На самом деле это не так, они нам просто не известны. Однако, для расчетов их принимают равными нулю и это не отражается на результатах. Например, энтальпия образования графита, как наиболее устойчивой формы углерода при стандартных условиях, равна нулю. Для алмаза и газообразного углерода аналогичные энтальпии отличаются от нуля: _ _ ∆Hº(C(граф))=0; ∆Hº(C(алмаз))=1,88 кДж/моль; _ ∆Hº(C(г)) = 718,4 кДж/моль. (1.52) Из этого примера видно, что необходимо учитывать в каком агрегатном и фазовом состояниях находятся реагенты и продукты реакций. Рассмотрим далее реакцию сгорания графита: C(граф) + О2(г) = СО2(г) +393,5кДж . (1.53) Это термохимическая форма записи уравнения реакции. В термодинамике тепловые эффекты в виде энтальпийных эффектов указываются рядом с уравнениями реакций. Так, в термодинамике уравнение (1.53) примет следующий вид: C(граф) + О2(г) = СО2(г); ∆Hр = – 393,5кДж. Для такой формы записи уравнений, как (1.53), ∆Hºр = – qºp. Учитывая закон сохранения энергии (в данном случае энтальпии), для уравнения (1.53) напишем следующее равенство: О  + О = ∆Hºр(СО2(г)) + 393,5кДж, (1.54) где нули – это стандартные энтальпии образования элементарных веществ: графита и кислорода. Из (1.54) следует: ∆  Hº(СО2(г)) = –393,5 кДж/моль. (1.55)Полученная величина названа стандартной энтальпией образования оксида углерода IV (химического соединения) из элементарных веществ. Стандартные энтальпии образования химических соединений из элементарных веществ в их стандартных состояниях при температуре 298К и давлении 1 атм не равны нулю и приводятся в различных таблицах термодинамических функций (например, приложение 1). Анализируя уравнения (1.53) – (1.55), можно показать, что для уравнений любых химических реакций выполняется уравнение (1.56): ∆Hºр =Σ∆Hº(продуктов) – Σ∆Hº(реагентов) . (1.56) Суммы энтальпий должны включать стехиометрические коэффициенты уравнений реакций в виде множителей соответствующих значений стандартных энтальпий образования веществ. В качестве примера вычислим ∆Hºр разложения кристаллического нитрата аммония на оксид азота I и газообразную воду: NН4NO3(ĸ) = N2O(г) + 2H2O(г). (1.57) По данным приложения 1 найдем стандартные энтальпии образования продуктов и реагентов реакции и их значения поставим в уравнение (1.56) (отметим также, что стехиометрические коэффициенты показывают числа молей реагентов и продуктов в сбалансированном уравнении реакции):  (NН4NO3(ĸ)) = – 365,4 кДж/моль, (N2O(г)) = 82,0 кДж/моль, (Н2O(г)) = – 241,8 кДж/моль, = 2 моль · (Н2O(г)) + 1 моль · (N2O(г)) –– 1 моль ·  = 2 моль · (– 241,8 кДж/моль)+ +1 моль · (82,0 кДж/моль) – 1 моль · (– 365,4 кДж/моль) = = – 36,2 кДж. (1.58) Видно, что реакция (1.57) является экзотермической. Если реакцию образования какого-либо соединения из элементарных веществ осуществить трудно, то для расчета энтальпии его образования можно воспользоваться значениями  ряда других реакций, из которых можно составить интересующую насреакцию. Например, можно рассчитать энтальпию образования серной кислоты Н2SO4 (ж), используя изменение энтальпии в реакциях сгорания серы до SO2 и окисления SO2 до SO3 , a также теплоту растворения SO3 в Н2О(ж) с образованием H2SO4(ж) при 298 К. Искомая реакция будет суммой реакций, приведенных ниже, а сумма изменений энтальпий в этих реакциях и есть энтальпия образования H2SO4(ж): S (тв) + О2(г)=SO2(г);  = – 296,89 кДж; S  02(г) + ½О2 (г)=SO3(г); = – 98,28 кДж ;S  03(г) + Н2О (ж) = Н2SО4 (ж); = – 130,29 кДж;Н2(г) + ½ О2 (г) = Н2О (ж); = – 285,85 кДж;S (тв) + 2 О2 (г) + H2(г) = H2SO4(ж); = – 811,32 кДж .Здесь изменения стандартных энтальпий суммируемых реакций вычислялось по (1.56). Для того, чтобы сравнивать тепловые эффекты одноименных фазовых переходов различных веществ, их относят к одному молю веществ при температурах фазовых переходов и давлении, равном 1 атм, и называют стандартными энтальпиями. Так, стандартной энтальпией плавления  называется изменение энтальпии, которым сопровождается плавление одного моля вещества при давлении 1 атм и температуре плавления данного вещества. Стандартной энтальпией парообразования  называется изменение энтальпии, которым сопровождается переход одного моля вещества из жидкого в газообразное состояние при давлении 1атм и температуре кипения данного вещества. Указанные фазовые переходы протекают с поглощением энергии, поэтому величины их стандартных энтальпий положительны: ∆Нºпл > 0 и  > 0. Обратные процессы: по отношению к плавлению – кристаллизация, - к парообразованию – конденсация, протекают при тех же условиях (давлении и температуре), что и прямые процессы, но с выделением теплоты. Поэтому значения их стандартных энтальпий отрицательны:  < 0 и  < 0. Абсолютные значения стандартных энтальпий прямых и обратных процессов одних и тех же веществ одинаковы. Поэтому в таблице 1.2 в качестве примера приведены только значения энтальпий плавления и парообразования и температуры фазовых переходов некоторых веществ.Таблица 1.2 Стандартные энтальпии плавления и парообразования
|