Лекция 1 введение
 Скачать 0.83 Mb. Скачать 0.83 Mb.
|
|
Лекция 1 ВВЕДЕНИЕ. Мы живем в техническую эпоху. На производстве и в повседневной жизни люди сталкиваются с многочисленными механизмами и электронными устройствами. Часто происходят природные и техногенные катастрофы: землетрясения, цунами, аварии на гидростанциях, атомных станциях и так далее. Главная цель любой науки, в том числе и физики - приведение в систему всего того, что нас окружает. Природа едина и ее изучение должно основываться на едином фундаменте, роль которого играет физика. Греческое слово «physis» в переводе означает «природа», поэтому наука о природе называется физикой. Весь окружающий мир представляет собой материю. Материя - это вся объективная реальность, существующая независимо от нашего сознания. В современной науке всё многообразие материи делят условно на следующие виды: физический вакуум, физические поля, элементарные частицы, атомы и молекулы, макроскопические тела различных размеров, планеты, звезды, галактики, системы галактик. Особый тип макроскопических тел - живая материя. Неотъемлемым свойством материи и формой ее существования является движение. Движение включает в себя все происходящие изменения и процессы, начиная от простого перемещения и кончая мышлением. Современная наука выделяет три основные группы форм движения материи: в неорганической природе, в живой природе, в обществе. Все формы движения связаны между собой. Механика - часть физики, изучающая закономерности механического движения. Механическое движение - это изменение взаимного расположения материальных точек, тел или их частей в пространстве с течением времени. Понятия пространства и времени являются основными не только в физике, но и для всего естествознания: всякое тело имеет пространственную протяженность, все события совершаются в определенной последовательности – время выражает последовательность состояний материи. Механика, изучающая движение макроскопических тел со скоростями, значительно меньшими скорости света в вакууме (с=3108м/с), называется классической механикой Галилея-Ньютона. Законы движения макроскопических тел со скоростями, сравнимыми со скоростью света, изучаются релятивисткой механикой, в основе которой лежит специальная теория относительности А.Эйнштейна. Законы движения и взаимодействия микрочастиц (атомов, элементарных частиц), описываются с помощью квантовой механики. Механика состоит из трех основных разделов: кинематики, динамики и статики. Статика изучает законы равновесия системы тел. Она подробно изучается в курсе теоретической механики. В механике не рассматривают вопросы внутреннего строения тел и физической природы взаимодействий между отдельными частями тел. Поэтому пользуются различными приближенными моделями. Простейшая модель – материальная точка. Материальной точкой называют тело, размерами которого можно пренебречь в данной задаче. Всякое тело можно рассматривать как систему материальных точек. Если деформации тела при его движении пренебрежимо малы, то используют модель абсолютно твердого тела. Физической величиной называется характеристика свойств тел или процессов, которые могут быть измерены количественно. Для измерения этих характеристик используют различные системы единиц, например систему «СИ». В механике основными являются «кг», «м», «с», «рад». 1. КИНЕМАТИКА ПОСТУПАТЕЛЬНОГО И ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ. Кинематика изучает движение тел, не рассматривая причины, вызывающие это движение. Положение тел в пространстве можно определить только по отношению к другим телам. . Тело отсчета – это тело, условно принятое за неподвижное. Система отсчета – совокупность системы координат и часов, связанных с телом отсчета. Важнейшими пространственными системами координат, применяемых в механике, являются прямоугольная декартова и системы криволинейных координат (цилиндрическая, сферическая, эллипсоидная). Пусть точка М движется в пространстве. Вектор, соединяющий начало (тело) отсчета с точкой М, есть радиус-вектор этой точки 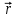 . Проекции вектора . Проекции вектора 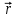 на оси x, y z есть составляющие радиус – вектора (рис. 1). Тогда можно записать: на оси x, y z есть составляющие радиус – вектора (рис. 1). Тогда можно записать: 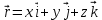 . Здесь . Здесь 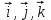 - орты (единичные векторы) вдоль осей x, y, z соответственно. - орты (единичные векторы) вдоль осей x, y, z соответственно.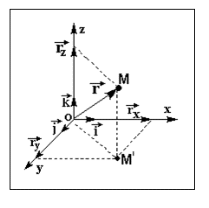 Рис.1 При движении материальной точки ее координаты и радиус-вектор изменяются с течением времени. Поэтому в общем случае можно записать: 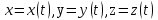 или или 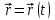 . .Эти уравнения называются кинематическими уравнениями движения материальной точки. Непрерывная кривая, которую описывает точка при своем движении относительно системы координат, называется траекторией. Скорость определяет быстроту изменения положения тела в пространстве. Средняя скорость 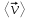 - это скорость за данный промежуток времени на данном участке траектории. Она равна отношению вектора перемещения - это скорость за данный промежуток времени на данном участке траектории. Она равна отношению вектора перемещения 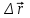 за время за время 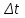 к этому промежутку времени к этому промежутку времени 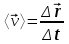 . .Мгновенная скорость 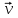 - это скорость в данный момент времени, в данном месте траектории. Она определяется как предел, к которому стремится - это скорость в данный момент времени, в данном месте траектории. Она определяется как предел, к которому стремится 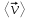 при при 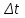 0. Отсюда следует 0. Отсюда следует 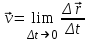 , , 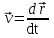 . .Векторная физическая величина, равная первой производной от радиус-вектора по времени называется скоростью. vx=dx/dt ; vy =dy/dt ; vz =dz/dt. 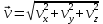 Величина, характеризующая изменение вектора скорости с течением времени есть ускорение 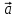 . Различают среднее и мгновенное ускорения. . Различают среднее и мгновенное ускорения.Среднее ускорение 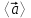 равно отношению изменения вектора скорости за время t к этому промежутку времени равно отношению изменения вектора скорости за время t к этому промежутку времени 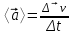 . .Мгновенное ускорение 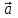 , т.е. ускорение в данный момент времени находится так: , т.е. ускорение в данный момент времени находится так: 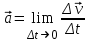 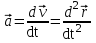 . .Вектор ускорения в данный момент времени определяется как первая производная от вектора скорости по времени или вторая производная от радиуса-вектора по времени. Поскольку скорость - величина векторная, она может изменяться как по величине, так и по направлению. При движении по криволинейной траектории, изменение вектора скорости 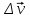 удобно представить в виде суммы двух слагаемых векторов удобно представить в виде суммы двух слагаемых векторов 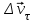 и и 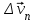 , т.е. , т.е. 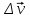 = =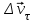 + +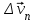 , (рис.2) , (рис.2)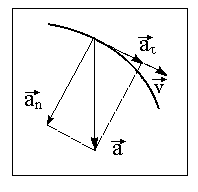 Рис. 2. где 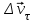 - изменение скорости по величине, - изменение скорости по величине, 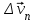 - изменение скорости по направлению за промежуток времени t. Поэтому вводят две составляющие ускорения: - изменение скорости по направлению за промежуток времени t. Поэтому вводят две составляющие ускорения: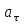 - тангенциальное или касательное ускорение, - тангенциальное или касательное ускорение, 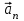 - нормальное ускорение. - нормальное ускорение.Полное ускорение 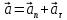 , где , где 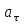 - характеризует изменение скорости только по величине, а - характеризует изменение скорости только по величине, а 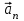 - характеризует изменение скорости только по направлению. - характеризует изменение скорости только по направлению. 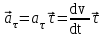 Тангенциальное ускорение 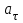 численно равно первой производной от модуля скорости по времени и направлено по касательной к траектории в данной точке (вдоль скорости, где τ – единичный вектор вдоль скорости). Вот почему численно равно первой производной от модуля скорости по времени и направлено по касательной к траектории в данной точке (вдоль скорости, где τ – единичный вектор вдоль скорости). Вот почему 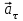 называется еще касательным ускорением. называется еще касательным ускорением.Учитывая, что 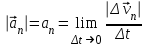 , можно получить: , можно получить: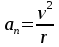 . .Вектор 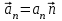 - перпендикулярен траектории в данной точке (направлен по радиусу кривизны траектории к центру окружности, - перпендикулярен траектории в данной точке (направлен по радиусу кривизны траектории к центру окружности, 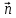 - единичный вектор в этом направлении. Полное ускорение: - единичный вектор в этом направлении. Полное ускорение: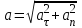 . .Вектор 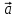 является диагональю прямоугольника со сторонами является диагональю прямоугольника со сторонами 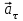 и и 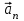 (рис. ). (рис. ).Частные случаи движения. 1. Равномерное прямолинейное движение: 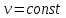 ; ;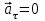 ; ;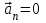 ; ; 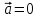 . . Уравнение движения: 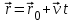 или или 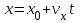 ; ; 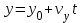 ; ; 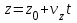 . .2. Прямолинейное равнопеременное движение: 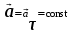 , , 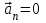 ; ; 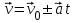 При равноускоренном движении а0, при равнозамедленном а0. Уравнение движения: 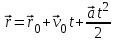 или или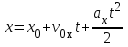 , , 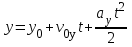 , , 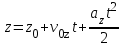 . .Уравнение пути, пройденного точкой при равнопеременном движении, можно получить при интегрировании формулы 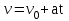 по времени от 0 до t. по времени от 0 до t.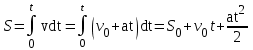 3. Прямолинейное переменное движение: 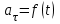 , , 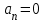 4. Равномерное криволинейное движение: 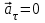 , , 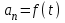 5. Равномерное движение по окружности: 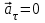 , , 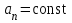 , , 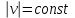 , , 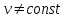 . .Кинематика вращательного движения материальной точки Вращательным называется такое движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения. Пусть точка или абсолютно твердое тело за время t, вращаясь вокруг неподвижной оси ОО’, перешло из положения 1 в 2, повернувшись на угол . Скалярная величина есть угол поворота (рис. 3 ). Элементарные (бесконечно малые) повороты можно рассматривать как векторы. Модуль такого вектора равен углу поворота d, а направление определяется по правилу правого винта: если винт вращать в направлении движения точки по окружности, то поступательное движение его острия указывает направление вектора 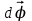 . Такие вектора, направление которых связывается с направлением вращения, называются псевдовекторами. . Такие вектора, направление которых связывается с направлением вращения, называются псевдовекторами.Быстрота вращения характеризуется вектором угловой скорости 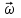 , направленной вдоль оси вращения как и , направленной вдоль оси вращения как и 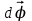 . . 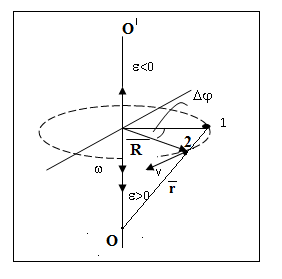 Рис. 3. Средняя угловая скорость: 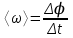 . . Мгновенная угловая скорость: 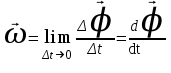 . . Изменение 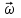 со временем определяет вектор углового ускорения со временем определяет вектор углового ускорения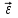 . .Среднее угловое ускорение: 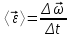 . . Мгновенное угловое ускорение: 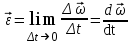 ; ; 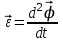 . . При вращении тела вокруг неподвижной оси изменение вектора 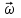 обусловлено только изменением его численного значения. Поэтому обусловлено только изменением его численного значения. Поэтому 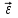 направлен вдоль оси вращения. Если вращение ускоренное, то направления направлен вдоль оси вращения. Если вращение ускоренное, то направления 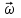 и и 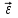 совпадают (0); если замедленное – то они противоположны (0). При равнопеременном движении точки по окружности (=const) совпадают (0); если замедленное – то они противоположны (0). При равнопеременном движении точки по окружности (=const) 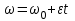 , , 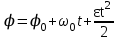 , ,где 0 – начальный угол поворота, 0 – начальная угловая скорость. Связь между линейными и угловыми кинематическими характеристиками. В векторном виде связь линейной скорости 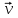 и угловой и угловой 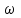 можно представить с помощью векторного произведения: можно представить с помощью векторного произведения: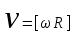 , , При вращении вокруг неподвижной оси угол между векторами 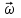 и и 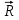 равен равен 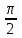 , следовательно: , следовательно:V = ω R. Отсюда: aτ = ɛ R и в векторном виде: 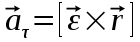 , , Для нормальной составляющей ускорения: 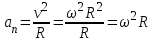 или или 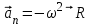 . Знак «минус» в формуле обусловлен противоположной направленностью векторов . Знак «минус» в формуле обусловлен противоположной направленностью векторов 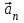 и и 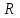 . . Если вращение равномерное, то 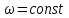 , и его можно характеризовать периодом вращения Т. Период – время одного полного оборота точки (тела) вокруг оси. , и его можно характеризовать периодом вращения Т. Период – время одного полного оборота точки (тела) вокруг оси.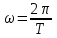 ; ; 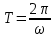 ; ; 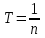 ; an= 4π2R/T2 ; an= 4π2n2 R. ; an= 4π2R/T2 ; an= 4π2n2 R. n – число оборотов в единицу времени, ω – циклическая частота вращения. При равномерном вращении 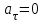 , an= 4π2n2 R. , an= 4π2n2 R. Лекция 2 2. ДИНАМИКА ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ Динамика – это раздел механики, который изучает движение совместно с причинами, вызывающими или изменяющими это движение. В основе динамики лежат три закона Ньютона, сформулированные им в 1687 г. Причиной изменения движения тел является силовое воздействие. Сила |
