|
|
Лекция 1 введение
Мы получили, что
О
тсюда видно, что длительность события, происходящего в некоторой точке, будет наименьшей в той инерциальной системе отсчета, относительно которой эта точка неподвижна. Например, часы, движущиеся относительно инерциальной системы отсчета, идут медленнее покоящихся часов, т.е. ход часов замедляется в той системе отсчета, относительно которой они движутся. Это замедление становится заметным при скоростях, близких к скорости света.
Эффект замедления хода времени подтверждается экспериментально в опытах с мюонами – нестабильными элементарными частицами. Среднее собственное время жизни мюона (по часам в той инерциальной системе отсчета, относительно которой он покоится) τ0 =2,2 мкс. Мюоны рождаются в верхних слоях атмосферы под действием первичного космического излучения и движутся относительно Земли со скоростями, близкими к скорости света. Если бы релятивистского эффекта замедления хода времени не было, то по отношению к земному наблюдателю мюон мог бы за время своей жизни пройти путь в атмосфере, не превышающий в среднем τ0с = 660 м. Иными словами, мюоны не могли бы достигать поверхности Земли. В действительности, мюоны регистрируются приборами, установленными на поверхности Земли, так как среднее время движущегося мюона по часам земного наблюдателя много больше τ0 и путь, проходимый мюоном за это время много больше 660 м.
4. Релятивистский закон сложения скоростей.
Рассмотрим движение материальной точки в системе К’ со скоростью u. Определим скорость этой точки в системе К если система К’ движется со скоростью v. Запишем проекции вектора скорости точки относительно систем К и К’:
K: ux=dx/dt, uy=dy/dt, uz=dz/dt; K’: ux’=dx’/dt’, uy’ =dy’/dt’, u’z=dz’/dt’.
Теперь нам нужно найти значения дифференциалов dx, dy, dz и dt. Продифференцировав преобразования Лоренца, получим:
 , , , ,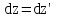 , ,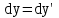 . .
Теперь мы сможем найти проекции скорости:
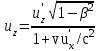 , , 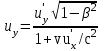 , ,  . .
Из этих уравнений видно, что формулы, связывающие скорости тела в разных системах отсчета (эаконы сложения скоростей) существенно отличаются от законов классической механики. При скоростях малых по сравнению со скоростью света, эти уравнения переходят в классические уравнения сложения скоростей.
Основной закон динамики релятивистской частицы.
Масса релятивистских частиц, т.е. частиц, движущихся со скоростями v
с не постоянна, а зависит от их скорости:  . Здесь m0 – это масса покоя частицы, т.е. масса, измеренная в той системе отсчета, относительно которой частица покоится. Эта зависимость подтверждена экспериментально. На основании ее рассчитывают все современные ускорители заряженных частиц (циклотрон, синхрофазотрон, бетатрон и т.д.). . Здесь m0 – это масса покоя частицы, т.е. масса, измеренная в той системе отсчета, относительно которой частица покоится. Эта зависимость подтверждена экспериментально. На основании ее рассчитывают все современные ускорители заряженных частиц (циклотрон, синхрофазотрон, бетатрон и т.д.).
Из принципа относительности Эйнштейна, утверждающего инвариантность всех законов природы при переходе от одной инерциальной системы отсчета к другой, следует условие инвариантности физических законов относительно преобразований Лоренца. Основной закон динамики Ньютона F=dP/dt=d(mv)/dt оказывается также инвариантным по отношению к преобразованиям Лоренца, если в нем справа стоит производная по времени от релятивистского импульса 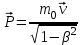 . .
Основной закон релятивистской динамики имеет вид:  , ,
и формулируется следующим образом: скорость изменения релятивистского импульса частицы, движущейся со скоростью близкой к скорости света, равна действующей на нее силе. При скоростях, намного меньших скорости света, полученное нами уравнение переходит в основной закон динамики классической механики. Основной закон релятивистской динамики инвариантен по отношению к преобразованиям Лоренца, но можно показать, что ни ускорение, ни сила, ни импульс сами по себе инвариантными величинами не являются. В силу однородности пространства в релятивистской механике выполняется закон сохранения релятивистского импульса: релятивистский импульс замкнутой системы не изменяется с течением времени.
Кроме всех перечисленных особенностей, основной и важнейший вывод специальной теории относительности сводится к тому, что пространство и время органически взаимосвязаны и образуют единую форму существования материи.
Взаимосвязь массы и энергии. Закон сохранения энергии в релятивистской механике.
Исследуя следствия основного закона релятивистской динамики, Эйнштейн пришел к выводу о том, что полная энергия двигающейся частицы равна  . Из этого уравнения следует, что даже неподвижная частица (когда =0) обладает энергией Е0 = m0с2, эту энергию называют энергией покоя (или собственной энергией). . Из этого уравнения следует, что даже неподвижная частица (когда =0) обладает энергией Е0 = m0с2, эту энергию называют энергией покоя (или собственной энергией).
Итак, универсальная зависимость полной энергии частицы от ее массы: Е = mс2 . Это фундаментальный закон природы – закон взаимосвязи массы и энергии. Согласно этому закону масса, находящаяся в покое, обладает огромным запасом энергии и любое изменение массы Δm сопровождается изменением полной энергии частицы ΔE=c2Δm.
Например, 1кг речного песка должен содержать 1(3,0∙108м/c)2 =9∙1016Дж энергии. Это вдвое больше еженедельного потребления энергии в США. Однако большая часть этой энергии недоступна, так как закон сохранения материи требует, чтобы общее число барионов (так называются элементарные частицы – нейтроны и протоны) в любой замкнутой системе оставалось постоянным. Отсюда следует, что суммарная масса барионов не меняется и, соответственно, она не может быть преобразована в энергию.
Но внутри атомных ядер нейтроны и протоны кроме энергии покоя обладают большой энергией взаимодействия друг с другом. В ряде таких процессов как синтез и деление ядер, часть этой потенциальной энергии взаимодействия может превращаться в добавочную кинетическую энергию, получаемых в реакциях, частиц. Это превращение и служит источником энергии ядерных реакторов и атомных бомб.
Правильность соотношения Эйнштейна можно доказать на примере распада свободного нейтрона на протон, электрон и нейтрино (с нулевой массой покоя): n → p + e- + ν. При этом суммарная кинетическая энергия конечных продуктов равна 1,25∙10-13 Дж. Масса покоя нейтрона превышает суммарную массу протона и электрона на 13,9∙10-31 кг. Этому уменьшению массы должна соответствовать энергия ΔE=c2Δm=(13,9∙10-31)(3,0∙108)2 =1,25∙10-15Дж. Она совпадает с наблюдаемой кинетической энергией продуктов распада.
В релятивистской механике не соблюдается закон сохранения массы покоя, но выполняется закон сохранения энергии: полная энергия замкнутой системы сохраняется, т.е. не изменяется с течением времени.
Общая теория относительности.
Спустя несколько лет после опубликования специальной теории относительности, Эйнштейном была разработана и окончательно сформулирована в 1915 г. общая теория относительности, которая представляет собой современную физическую теорию пространства, времени и тяготения.
Главным предметом общей теории относительности является гравитационное взаимодействие, или тяготение. В законе всемирного тяготения Ньютона подразумевается, что сила тяготения действует мгновенно. Такое утверждение противоречит одному из основных принципов теории относительности, а именно: ни энергия, ни сигнал не могут распространяться быстрее скорости света. Таким образом, Эйнштейн столкнулся с проблемой релятивистской теории тяготения. Для решения этой проблемы необходимо было также ответить на вопрос: различаются ли гравитационная масса (входящая в закон Всемирного тяготения) и инертная масса (входящая во второй закон Ньютона)? Ответ на этот вопрос может дать только опыт. Вся совокупность опытных фактов указывает на то, что инертная и гравитационная массы тождественны. Известно, что силы инерции аналогичны силам тяготения: находясь внутри закрытой кабины, никакими опытами нельзя установить, чем вызвано действие на тело силы mg – тем ли, что кабина движется с ускорением g, либо тем, что неподвижная кабина находится вблизи поверхности Земли. Вышесказанное представляет собой так называемый принцип эквивалентности: поле тяготения по своему проявлению тождественно ускоряющейся системе отсчета. Это утверждение и было положено Эйнштейном в основу общей теории относительности.
В своей теории Эйнштейн получил, что свойства пространства и времени связаны более сложными соотношениями, чем соотношения Лоренца. Вид этих связей зависит от распределения материи в пространстве, часто образно говорят, что материя искривляет пространство и время. Если материи нет на больших расстояниях от точки наблюдения или искривление пространства‑времени мало, то можно с удовлетворительной точностью использовать соотношения Лоренца.
Явление гравитации (притяжение тел имеющих массу) Эйнштейн объяснил тем, что массивные тела так искривляют пространство, что естественное движение других тел по инерции происходит по тем же траекториям, как если бы существовали силы притяжения. Таким образом, Эйнштейн решил проблему совпадения гравитационной и инертной массы путем отказа от использования понятия сил гравитации.
Следствия, полученные из общей теории относительности (теории гравитации), предсказали наличие новых физических явлений вблизи массивных тел: изменение хода времени; изменение траекторий других тел, не объясняемое в классической механике; отклонение лучей света; изменение частоты света; необратимое притяжение всех форм материи к достаточно массивным звездам и др. Все эти явления были обнаружены: изменение хода часов наблюдали при полете самолета вокруг Земли; траектория движения самой близкой к Солнцу планеты – Меркурия объясняется только этой теорией, отклонение лучей света наблюдается для лучей, идущих от звезд к нам вблизи Солнца; изменение частоты или длины волны света также обнаружено, этот эффект называется гравитационным красным смещением, он наблюдается в спектральных линиях Солнца и тяжелых звезд; необратимым притяжением материи к звездам объясняют наличие «черных дыр» ‑ космических звездных объектов, поглощающих даже свет. Кроме этого, множество космологических вопросов находит объяснение в общей теории относительности.
Лекция 9
МОЛЕКУЛЯРНО-КИНЕТИЧЕСКАЯ ТЕОРИЯ ИДЕАЛЬНЫХ ГАЗОВ
Термодинамические параметры
Мысленно выделенная макроскопическая система, рассматриваемая методами термодинамики, называется термодинамической системой. Все тела, не включенные в состав исследуемой системы, называются внешней средой. Состояние системы задается термодинамическими параметрами, напр. давление р, температура Т и удельный объем v. Различают два типа термодинамических параметров: экстенсивные и интенсивные. Экстенсивные параметры пропорциональны количеству вещества в системе, а интенсивные не зависят от количества вещества и массы системы. Интенсивными параметрами являются давление, температура, удельный объем и др., а экстенсивными – объем, энергия, энтропия.
Температура системы является мерой интенсивности теплового движения и взаимодействия частиц, образующих систему. В этом состоит молекулярно-кинетический смысл температуры. В настоящее время существует две температурных шкалы – термодинамическая (градуированная в Кельвинах (К)) и Международная практическая (градуированная в градусах Цельсия (˚С)). 1˚С = 1К. Связь между термодинамической температурой Т и температурой по Международной практической шкале имеет вид: Т = t + 273,15˚С.
Всякое изменение состояния термодинамической системы, характеризующееся изменением ее параметров, называется термодинамическим процессом. Термодинамический процесс называется равновесным, если при этом система проходит ряд бесконечно близких равновесных состояний. Равновесное состояние – это такое состояние, в которое система приходит в конце концов при неизменных внешних условиях и дальше остается в этом состоянии сколь угодно долго. Реальный процесс изменения состояния системы будет тем ближе к равновесному, чем медленнее он совершается.
Лекция 9
МОЛЕКУЛЯРНО-КИНЕТИЧЕСКАЯ ТЕОРИЯ ИДЕАЛЬНЫХ ГАЗОВ
Термодинамические параметры
Мысленно выделенная макроскопическая система, рассматриваемая методами термодинамики, называется термодинамической системой. Все тела, не включенные в состав исследуемой системы, называются внешней средой. Состояние системы задается термодинамическими параметрами, напр. давление р, температура Т и удельный объем v. Различают два типа термодинамических параметров: экстенсивные и интенсивные. Экстенсивные параметры пропорциональны количеству вещества в системе, а интенсивные не зависят от количества вещества и массы системы. Интенсивными параметрами являются давление, температура, удельный объем и др., а экстенсивными – объем, энергия, энтропия.
Температура системы является мерой интенсивности теплового движения и взаимодействия частиц, образующих систему. В этом состоит молекулярно-кинетический смысл температуры. В настоящее время существует две температурных шкалы – термодинамическая (градуированная в Кельвинах (К)) и Международная практическая (градуированная в градусах Цельсия (˚С)). 1˚С = 1К. Связь между термодинамической температурой Т и температурой по Международной практической шкале имеет вид: Т = t + 273,15˚С.
Всякое изменение состояния термодинамической системы, характеризующееся изменением ее параметров, называется термодинамическим процессом. Термодинамический процесс называется равновесным, если при этом система проходит ряд бесконечно близких равновесных состояний. Равновесное состояние – это такое состояние, в которое система приходит в конце концов при неизменных внешних условиях и дальше остается в этом состоянии сколь угодно долго. Реальный процесс изменения состояния системы будет тем ближе к равновесному, чем медленнее он совершается.
Уравнение состояния идеального газа
В молекулярно-кинетической теории широко используется физическая модель идеального газа. Это вещество, находящееся в газообразном состоянии, для которого выполняются следующие условия:
Собственный объем молекул газа пренебрежимо мал по сравнению с объемом сосуда.
Между молекулами газа отсутствуют взаимодействия, кроме случайных столкновений.
Столкновения молекул газа между собой и со стенками сосуда абсолютно упругие.
Поведение идеальных газов описывается рядом законов.
Закон Авогадро: В одном моле различных веществ содержится одно и то же число молекул, называемое числом Авогадро NA= 6,022∙1023моль-1 .
Клапейрон и Менделеев вывели уравнение состояния идеального газа – уравнение Менделеева– Клапейрона.
pV=
С учетом того, что число молекул в массе m равно N=Na∙ν, а концентрация молекул n=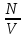 , можно получить: , можно получить:
p=nkT
где k =R/NA = 1,38∙10-23 Дж/К – постоянная Больцмана.
Основное уравнение молекулярно-кинетической теории газа записывается так:
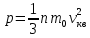 , ,
где  . .
Cредняя энергия поступательного движения молекул:
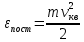 , тогда p= , тогда p=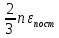
Если E – суммарная кинетическая энергия поступательного движения всех молекул: pV=
Для вывода второго следствия воспользуемся первым следствием и уравнением
Менделеева-клапейрона.
pV= E= E=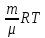
Отсюда: 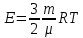
Энергия молекул Е в веществе пропорциональна количеству вещества в системе и температуре.
Найдем среднюю кинетическую энергию поступательного движения одной молекулы ‹ εпост›, учитывая, что k =R/NA получим:
О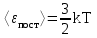
тсюда следует, что средняя кинетическая энергия хаотического поступательного движения молекул идеального газа пропорциональна его абсолютной температуре и зависит только от нее, т.е. температура есть количественная мера энергии теплового движения молекул. При одинаковой температуре средние кинетические энергии молекул любого газа одинаковы. При Т=0К ‹εпост› = 0 и поступательное движение молекул газа прекращается, однако анализ различных процессов показывает, что Т = 0К – недостижимая температура.
Учитывая, что ‹εпост› = 3kT/2, р = 2n‹ εпост›/3, получим отсюда: р = nkT.
Мы получили уже знакомый нам вариант уравнения Менделеева-Клапейрона, выведенный в данном случае из понятий молекулярно-кинетической теории статистическим методом. Последнее уравнение означает, что при одинаковых температуре и давлении все газы содержат в единице объема одинаковое число молекул.
При выводе основного уравнения молекулярно-кинетической теории отмечалось, что молекулы имеют различные скорости. В результате многократных соударений скорость каждой молекулы меняется со временем по модулю и по направлению. Из-за хаотичности теплового движения молекул все направления являются равновероятными, а средняя квадратичная скорость остается постоянной. Мы можем записать
 Отсюда: Отсюда:
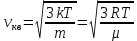
Барометрическая формула
При выводе основного уравнения молекулярно-кинетической теории предполагалось, что если на молекулы газа не действуют внешние силы, то молекулы равномерно распределены по объему. Однако молекулы любого газа находятся в потенциальном поле тяготения Земли. Тяготение, с одной стороны, и тепловое движение молекул, с другой, приводят к некоторому стационарному состоянию газа, при котором концентрация молекул газа и его давление с высотой убывают.
Пусть на высоте h давление равно р=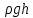 , а на высоте (h+dh) - (p-dp)= , а на высоте (h+dh) - (p-dp)= . .
Вычтем из второго уравнения первое:
-dp=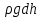
Из уравнения состояния газа плотность 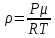 , тогда: , тогда:
-dp= или или  . .
Возьмем интеграл от левой и правой стороны уравнения:
 lnp = ln lnp = ln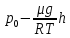 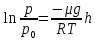
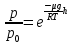
p=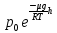
Данное выражение называется барометрической формулой. Она позволяет найти атмосферное давление в зависимости от высоты, или высоту, если известно давление.
Закон Больцмана о распределении частиц во внешнем потенциальном поле
Если воспользоваться выражением р = nkT, то можно перейти от барометрической формулы к выражению для концентрации молекул:
n=
здесь n – концентрация молекул на высоте h, n0 – то же у поверхности Земли. Так как μ = m0NA , где m0 – масса одной молекулы, а R = k NA, то мы получаем выражение для потенциальная энергия одной молекулы в поле тяготения Епот = m0gh. Отсюда:
n=
Так как средняя энергия поступательного движения молекулы
kT, то концентрация молекул на определенной высоте зависит от соотношения потенциальной энергии и ‹εпост›.

Полученное выражение называется распределением Больцмана для внешнего потенциального поля. Из него следует, что при постоянной температуре плотность газа (с которой связана концентрация) больше там, где меньше потенциальная энергия его молекул.
Распределение Максвелла молекул идеального газа по скоростям
Постоянство ‹υкв› объясняется тем, что в газе устанавливается стационарное, не меняющееся со временем распределение молекул по скоростям, которое подчиняется определенному статистическому закону. Этот закон теоретически был выведен Максвеллом. Он представил функцию f(u), называемую функцией распределения молекул по скоростям. Если разбить диапазон всех возможных скоростей молекул на малые интервалы, равные du, то на каждый интервал скорости будет приходиться некоторое число молекул dN(u), имеющих скорость, заключенную в этом интервале.
Функция f(v) определяет относительное число молекул, скорости которых лежат в интервале от u до u+ du. Это число – f(v)= . Применяя методы теории вероятностей, Максвелл нашел вид для функции f(u) . Применяя методы теории вероятностей, Максвелл нашел вид для функции f(u)
|
|
|
 Скачать 0.83 Mb.
Скачать 0.83 Mb. ,
, ,
,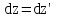 ,
,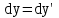 .
. 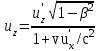 ,
, 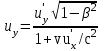 ,
,  .
.

 . Здесь m0 – это масса покоя частицы, т.е. масса, измеренная в той системе отсчета, относительно которой частица покоится. Эта зависимость подтверждена экспериментально. На основании ее рассчитывают все современные ускорители заряженных частиц (циклотрон, синхрофазотрон, бетатрон и т.д.).
. Здесь m0 – это масса покоя частицы, т.е. масса, измеренная в той системе отсчета, относительно которой частица покоится. Эта зависимость подтверждена экспериментально. На основании ее рассчитывают все современные ускорители заряженных частиц (циклотрон, синхрофазотрон, бетатрон и т.д.).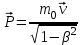 .
.  ,
, . Из этого уравнения следует, что даже неподвижная частица (когда =0) обладает энергией Е0 = m0с2, эту энергию называют энергией покоя (или собственной энергией).
. Из этого уравнения следует, что даже неподвижная частица (когда =0) обладает энергией Е0 = m0с2, эту энергию называют энергией покоя (или собственной энергией). 
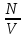 , можно получить:
, можно получить: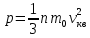 ,
,  .
.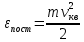 , тогда p=
, тогда p=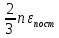

 E=
E=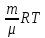
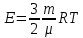
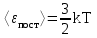
 Отсюда:
Отсюда: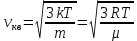
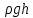 , а на высоте (h+dh) - (p-dp)=
, а на высоте (h+dh) - (p-dp)= .
.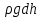
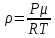 , тогда:
, тогда: или
или  .
. lnp = ln
lnp = ln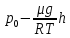
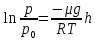
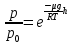
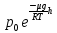



 . Применяя методы теории вероятностей, Максвелл нашел вид для функции f(u)
. Применяя методы теории вероятностей, Максвелл нашел вид для функции f(u)