|
|
Лекция 1 введение

Данное выражение - это закон распределении молекул идеального газа по скоростям.
Эта формула позволяет оценить вероятность того, что молекула данного газа при данной температуре имеет определенную скорость v. Очевидно, что вероятность зависит от температуры Т и массы молекулы m0.
Скорость uв, при которой функция f(u) достигает максимума, называется наиболее вероятной скоростью:
С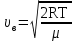
редняя арифметическая скорость молекулы определяется по формуле:
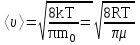
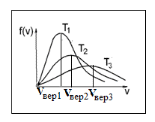
На рисунке представлены графики функции распределения молекул идеального газа по скоростям (максвелловское распределение), полученные при температурах Т1, Т2, Т3. Здесь 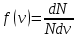 – доля молекул, скорости которых заключены в диапазоне скоростей от v до (v+dv) в расчете на единицу этого интервала. – доля молекул, скорости которых заключены в диапазоне скоростей от v до (v+dv) в расчете на единицу этого интервала.
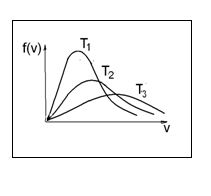
Ясно, что площади под кривыми равны вероятности нахождения частицы в состоянии со скоростью v в диапазоне от 0 до ∞. И эта вероятность равна 1 при любой температуре.
Как соотносятся температуры газа для состояний, соответствующих графикам максвелловского распределения молекул идеального газа по скоростям, представленным на рисунке? Количество газа во всех случаях одинаково.
Н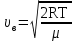
аиболее вероятная скорость определяется по формуле
Очевидно, что скорость пропорциональна квадратному корню из температуры.
Лекция 10
ОСНОВЫ ТЕРМОДИНАМИКИ
Внутренняя энергия
Важной характеристикой любой термодинамической системы является ее внутренняя энергия – энергия хаотического теплового движения частиц системы - молекул, атомов и энергия их взаимодействия. К внутренней энергии не относится кинетическая энергия движения системы как целого и потенциальная энергия системы во внешних полях. Внутренняя энергия системы в определенном состоянии не зависит от того, как система пришла в это состояние (т.е. от пути перехода), а определяется только значениями термодинамических параметров в этих состояниях.
Введем понятие числа степеней свободы – это число независимых переменных (координат), полностью определяющих положение системы в пространстве. Например, молекулу одноатомного газа можно рассматривать как материальную точку, обладающую тремя степенями свободы поступательного движения (координаты x,y,z), iпост=3. Молекула двухатомного газа, рассматриваемая в классической механике как совокупность двух материальных точек, жестко связанных между собой, имеет 3 поступательные степени свободы iпост=3, описывающие положение центра масс молекулы, и 2 вращательные степени свободы iвр=2 для закрепления ориентации молекулы в пространстве. Если связь между атомами упругая, то имеется 1 колебательная степень свободы iколеб=1.
Трехатомные молекулы, в которых атомы связаны жестко между собой, имеют 3 поступательные степени свободы iпост=3, 3 вращательные степени свободы iвр=3, а если связи между атомами упругие – еще 3 колебательные степени свободы iколеб=3.
В классической статистической физике существует закон Больцмана о равномерном распределении энергии по степеням свободы: для статистической системы, находящейся в состоянии термодинамического равновесия, на каждую поступательную и вращательную степени свободы приходится в среднем кинетическая энергия, равная кТ/2, а на каждую колебательную степень свободы – кТ. Колебательная степень свободы обладает вдвое большей энергией, так как на нее приходится не только кинетическая, но и потенциальная энергия взаимодействия. Таким образом, средняя энергия любой молекулы ‹ε› = ikT/2, где i - это сумма поступательных, вращательных и удвоенного числа колебательных степеней свободы.
Из этого закона получаем, что внутренняя энергия UМ одного моля идеального газа равна:
UМ=ikTNA/2 = iRT/2,
а внутренняя энергия U газа массы m равна:
U=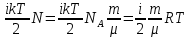 . .
Первое начало термодинамики
Обмен энергией между термодинамической системой и внешней средой может осуществляться двумя качественно различными способами: путем совершения работы и путем теплообмена.
Изменение энергии системы, происходящее под действием сил измеряется работой. Если термодинамическая система совершает работу против внешних сил, то работа считается положительной (А>0). Если работу над системой совершают внешние силы, то она считается отрицательной (А< 0).
Изменение энергии системы, происходящее в результате теплообмена, определяется количеством переданной или отнятой теплоты Q.
Итак, работа и теплота – это две формы передачи энергии от одних тел другим.
ΔU = Q – A или Q = ΔU + A, где А – работа газа.
В дифференциальной форме (для малых изменений величин) это запишется следующим образом:
δQ = dU + δA ,
где δQ - бесконечно малое количество теплоты, переданное системе, dU – бесконечно малое изменение внутренней энергии системы, δA – элементарная работа, совершенная системой. Это уравнение выражает первое начало термодинамики: теплота, подводимая к системе, расходуется на изменение ее внутренней энергии и на совершение работы против внешних сил. Знак δ в δQ и δА означают, что данные элементарные приращения не являются полными дифференциалами и, следовательно, А и Q не являются функциями состояния.
Теплоемкость
Одним из основных свойств тел, которое широко используется в термодинамике, является теплоемкость. Теплоемкостью тела называется физическая величина, численно равная отношению теплоты δQ, сообщаемой телу, к изменению температуры тела в рассматриваемом термодинамическом процессе. Теплоемкость тела зависит от его химического состава, массы и термодинамического состояния, а также от вида процесса, в котором поступает теплота. Тепловые свойства однородных тел характеризуются понятиями удельной и молярной теплоемкостей.
Ст=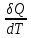
Удельная теплоемкость вещества – величина, численно равная количеству теплоты, необходимому для нагревания единицы массы вещества на 1 Кельвин при данном процессе, единица измерения – Дж/(кг∙К):
c=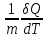
М

олярная теплоемкость – величина, равная количеству теплоты, необходимому для нагревания одного моля вещества на 1К , т.е. С =сμ, где μ – молярная масса вещества.
C=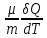
Теплоемкости одного и того же вещества при разных термодинамических процессах нагревания различаются.
1) Если газ нагревается при постоянном объеме, то есть в изохорном процессе, A=0, тогда:
Сv=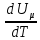
2) Если газ нагревается при постоянном давлении, то есть в изобарном процессе,
тогда: СP=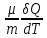 = =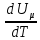 + + 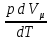 =CV + =CV +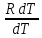 =Cv +R =Cv +R
Или СP=Cv +R, эта формула получила название уравнения Майера.
|
|
|
 Скачать 0.83 Mb.
Скачать 0.83 Mb.