Лекция 1 введение

• Название: Лекция 1 введение
• Дата: 15.06.2022
• Размер: 0.83 Mb.
• Имя файла: %D0%BB%D0%B5%D0%BA%D1%86%D0%B8%D0%B8%D0%B7%D0%B0%D0%BE%D1%87%D0%.docx
• Тип: Лекция; #593962
• страница: 9 из 10

 Применение первого начала термодинамики к изопроцессам

Различают следующие виды термодинамических процессов:
1. Изохорный - это процесс, протекающий при постоянном объеме V=const. При изохорном процессе газ не совершает работы над внешними телами. В изохорном процессе вся теплота идет на увеличение внутренней энергии:

δQ = dU.

2. Изобарный – это процесс, протекающий при постоянном давлении. Первое начало термодинамики для изобарного процесса δQ = dU + δA.

3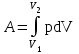
. Изотермический – это процесс, протекающий при постоянной температуре. Кривая, построенная в координатах (р, V), называется изотермой. Работа, совершаемая газом, определяется интегралом, при этом Т не меняется, то есть dU = 0:

и первое начало термодинамики для изотермического процесса примет вид:

δQ = δА.

Теплоемкость при изотермическом процессе С_Т =δQ/dT=δQ/0 = ∞ и, казалось бы, не имеет смысла. Изотермический процесс осуществляется при наличии термостата (внешней среды или тела с большим запасом внутренней энергии, находящемся при той же температуре).

Найдем работу изотермического расширения газа, учитывая, что все количество теплоты, сообщаемое газу, расходуется на совершение им работы против внешних сил и не изменяет его температуру. Учитывая формулу для работы и уравнение Менделеева-Клайперона, получаем:

A=

Примерами изотермических процессов являются закалка и отжиг сталей в процессе их изготовления. Существуют автомобили и вагоны – рефрижераторы, служащие для перевозки скоропортящихся продуктов. Они имеют теплоизолированный кузов и холодильники для поддержания внутри постоянной температуры и поэтому процесс перевозки продуктов в таких условиях можно назвать изотермическим..

4. Адиабатический процесс. Адиабатическим называется процесс, при котором отсутствует теплообмен между системой и окружающей средой, т.е.

δQ = 0, Q = const.

Так как δQ = 0, первое начало термодинамики имеет вид:

δА= -dU

т.е. работа газа совершается за счет внутренней энергии газа. Если газ расширяется, то δА>0, dU<0 и температура газа уменьшается. Если происходит сжатие газа, то δА<0 и dU>0. То есть работу над газом совершают внешние силы, внутренняя энергия (а, значит, и температура) газа повышается. Реализовать адибатический процесс можно, если проводить его либо при хорошей теплоизоляции от окружающей среды, либо быстро за короткое время, при котором теплообмен будет мал.

Уравнение адиабатического процесса (уравнение Пуассона) имеет вид:

рV^γ = const,

где γ = С_р /C_v – коэффициент (показатель адиабаты).

Теплоемкость при адиабатическом процессе С_Q= dQ/ΔT=0/ΔT=0.

Адиабатические процессы широко распространены в технике, например, в двигателях внутреннего сгорания. Истечение газов через сопла реактивных двигателей также может считаться адиабатическим процессом, поскольку происходит очень быстро.
Лекция 11.

Второе начало термодинамики

Термодинамический процесс называется обратимым, если он может происходить как в прямом, так и в обратном направлении, а в окружающей среде при этом не происходит никаких изменений. Всякий процесс, не удовлетворяющий этим условиям, является необратимым.

Если система, пройдя через ряд состояний, возвращается в исходное, то такой процесс называется круговым процессом, или циклом.

Циклы лежат в основе работы всех тепловых машин – двигателей внутреннего сгорания, паровых и газовых турбин, холодильников. В результате кругового процесса система может теплоту как получать, так и отдавать.

Нагревателем называют тело, сообщающее рассматриваемой термодинамической системе энергию в форме теплоты Q₁. Холодильником называют тело, получающее от рассматриваемой термодинамической системы теплоту Q₂. Рабочим телом называют термодинамическую систему, совершающую круговые процессы. Работа, совершаемая за цикл, равна теплоте Q = Q₁ ‑ Q₂ = А.

Термическим (термодинамическим) коэффициентом полезного действия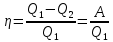



Цикл Карно

Циклом Карно называется прямой круговой процесс, состоящий из двух изотермических процессов 1 – 1^’ и 2 – 2^” , и двух адиабатических процессов 1^” - 2 и 2^” – 1. В процессе 1 – 1^’ рабочее тело получает теплоту Q₁  от нагревателя, в процессе 2 – 2^” отдает теплоту Q₂ холодильнику.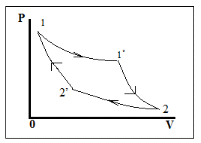



Рис.
Теорема Карно: термический коэффициент полезного действия обратимого цикла Карно не зависит от природы рабочего тела и является только функцией абсолютной температуры нагревателя Т₁ и холодильника Т₂ .



Термический к.п.д. произвольного (обратимого или необратимого) цикла не может превосходить к.п.д. цикла Карно, проведенными между температурами T_max и T_min.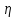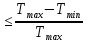

=
Второй закон термодинамики

Энтропия

Для описания термодинамических процессов одного первого начала термодинамики недостаточно, потому что оно не позволяет определять направление протекания процессов. Например, процесс самопроизвольной передачи теплоты от холодного тела горячему первым началом не запрещен, однако опыты показывают, что он не происходит. Итак, необходимо определить условия, при которых возможны превращения энергии из одного вида в другой, что позволило бы узнать направления протекания процессов.

В термодинамике, кроме внутренней энергии, существует еще несколько функций состояния системы. Особое место среди них занимает энтропия S. Энтропия как раз и является той величиной, которая позволяет прогнозировать возможность и направление протекания процессов. Энтропия - понятие, впервые введенное в термодинамике для определения меры необратимого рассеяния энергии немецким физиком Р.Клаузиусом в 1865г.

Пусть δQ – элементарное количество теплоты, сообщаемое системе каким-либо нагревателем с постоянной температурой Т. Если процесс равновесный (обратимый), то температура системы тоже равна Т. Отношение 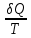называется приведенным количеством теплоты и равно изменению энтропии dS.

Поскольку Т всегда > 0, то видно, что δQ и dS имеют один и тот же знак. Это позволяет по характеру изменения энтропии судить о направлении процесса теплообмена и прогнозировать его возможность. При нагревании тела δQ > 0 и его энтропия возрастает (dS > 0), при охлаждении - энтропия убывает. Если δQ=0 (обратимый адиабатический процесс), то dS = 0 и S = const, то есть энтропия остается постоянной.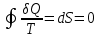



Энтропия, подобно внутренней энергии, является функцией состояния системы. Энтропия системы равна сумме энтропий всех тел, входящих в систему. Для изолированной системы энтропия в любом обратимом процессе не изменяется и S = const. В термодинамике доказывается, что в необратимом процессе энтропия системы может только возрастать: dS 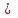0. Объединяя два последних условия, мы получаем, что энтропия замкнутой системы может либо возрастать, либо оставаться постоянной:

dS ≥ 0

Это неравенство Клаузиуса является формулировкой второго начала термодинамики.

Другая формулировка 2 закона: Теплота никогда не может переходить сама собой от тел с более низкой температурой к телам с более высокой температурой.

С точки зрения молекулярной физики, энтропия является мерой разупорядоченности системы, т.е. чем система более хаотична, тем ее энтропия выше. С этой точки зрения второе начало термодинамики утверждает, что в замкнутой системе, при отсутствии внешних воздействий любая система стремится перейти в состоянии максимальной разупорядоченности. Такое состояние является наиболее вероятным, поэтому энтропию S можно связать с вероятностью W состояния системы соотношением Больцмана

S=k lnW,

а второе начало объяснять стремлением системы находиться в наиболее вероятном состоянии.

По определению, W 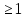, так как W – число способов, которыми может быть осуществлено данное состояние. Если состояние осуществляется одним способом, то

S=k ln1 = 0

Состояние равновесия – самое вероятное, при этом число микросостояний - максимально.

Так как реальные системы необратимы, то все процессы в замкнутой системе ведут к увеличению энтропии.

Явление увеличения беспорядка можно легко наблюдать при добавлении в воду капли туши. Если не воздействовать на такую систему извне, то через небольшое время тушь полностью перемешается с водой, обратный процесс – процесс собирания частичек туши в каплю, хотя в принципе он и возможен, никогда не наблюдается.
Третий закон термодинамики.

Третий закон термодинамики по другому называют законом Нернста – Планка:

Энтропия всех тел в состоянии равновесия стремится к 0 по мере приближения температуры к 0 Кельвина:

limS=0, если Т⁰ К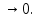

Явления переноса

Беспорядочность теплового движения молекул газа или жидкости, непрерывные столкновения между ними приводят к постоянному перемешиванию частиц и к изменению их скоростей и энергий. Если в веществе имеется пространственная неоднородность плотности или температуры, то со временем, согласно второму началу термодинамики, происходит обязательное выравнивание этих неоднородностей. В среде возникают потоки энергии, вещества, а также импульса упорядоченного движения частиц. Эти потоки являются физической основой особых процессов, объединенных под общим названием явления переноса. К этим явлениям относится теплопроводность (обусловлена переносом энергии), диффузия (обусловлена переносом массы) и внутреннее трение (обусловлено переносом импульса).

1. Теплопроводность

Теплопроводность – это явление переноса внутренней энергии (теплоты) при наличии неоднородности в распределении температуры. В простейшем одномерном случае, когда температура газа меняется только в одном направлении, например, вдоль оси х, перенос внутренней энергии газа путем теплообмена описывается законом Фурье:

j_E = -λ ∙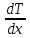

где j_E - это плотность теплового потока, т.е. величина, равная энергии, переносимой в форме теплоты в единицу времени через единичную площадку, перпендикулярную оси х. Величина λ называется теплопроводностью или коэффициентом теплопроводности, 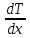 – градиент температуры, показывающий, как изменяется температура на единицу длины х перпендикулярно рассматриваемой площадке. Знак «минус» показывает, что перенос энергии происходит в направлении убывания температуры. Теплопроводность λ численно равна плотности теплового потока при единичном градиенте температуры.

В общем случае закон Фурье имеет вид: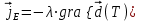

.

Здесь 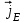- вектор плотности теплового потока, направление которого совпадает с направлением переноса энергии. Согласно молекулярно-кинетической теории газов λ= 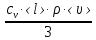, где c_V – удельная теплоемкость при постоянном объеме, ρ – плотность газа, ‹υ› - средняя скорость теплового движения молекул, ‹ℓ› - средняя длина свободного пробега молекул
2. Внутреннее трение (вязкость)


Явление внутреннего трения заключается в ускорении и замедлении слоев газа или жидкости вследствие наличия неоднородности скорости. Между слоями, двигающимися параллельно друг другу с различными по величине скоростями (ламинарное движение), из-за хаотического теплового движения возникает обмен молекулами с разными импульсами. Это приводит к тому, что медленно перемещающиеся слои тормозят более быстро движущиеся слои и наоборот. При этом возникают силы трения или силы вязкости, направленные по касательной к поверхности соприкосновения слоев. В результате этого импульс слоя, движущегося быстрее, уменьшается, а движущегося медленнее – увеличивается, что и приводит к торможению быстрого слоя и ускорению медленного. Формулу для силы внутреннего трения между двумя слоями газа или жидкости предложил Ньютон:

Здесь η - коэффициент динамической вязкости, 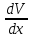- градиент скорости, показывающий быстроту изменения скорости в направлении, перпендикулярном движению, S - площадь, на которую действует сила.

Согласно молекулярно-кинетической теории газов вязкость газов можно вычислить по формуле: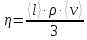



3. Диффузия
Диффузией называется явление самопроизвольного взаимного проникновения и перемешивания частиц соприкасающихся газов, жидкостей и даже твердых тел при наличии неоднородности распределения частиц разного сорта. В смесях диффузия вызывается наличием разных концентраций молекул компонентов смеси в разных частях объема. В химически чистых веществах она возникает вследствие неоднородности распределения плотности вещества, такой процесс носит название самодиффузии. В химически однородном газе явление диффузии подчиняется закону Фика :

j_m = -D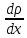

j_m -плотность потока массы ( равна массе вещества, диффундирующего в единицу времени через единичную площадку, перпендикулярную оси х, т.е. j_m=Δm /( Δt ∙ S), D -  коэффициент диффузии, 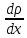- градиент плотности, показывающий, как изменяется плотность на единицу длины х в направлении нормали к единичной площадке. Знак «минус» указывает, что перенос массы происходит в направлении убывания плотности. Коэффициент диффузии численно равен плотности потока массы при градиенте плотности, равном единице. Согласно кинетической теории газов D = .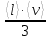

В общем случае трехмерной диффузии закон Фика имеет вид: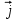

= - D∙ grad(ρ).

Реальные газы

Модель идеального газа позволяет описывать поведение реальных газов при достаточно высоких температурах и низких давлениях, когда можно пренебречь размерами молекул и их взаимодействием друг с другом. Однако при повышении давления необходимо учитывать, что молекулы не являются материальными точками, а имеют определенный объем. Необходимо учитывать также силы межмолекулярного взаимодействия. Эти силы имеют электромагнитную и квантовую природу. Между молекулами вещества в любом агрегатном состоянии действуют силы взаимного притяжения, проявляющиеся в способности сопротивляться растяжению, образовывать капли и т.д. Кроме того, относительно малая сжимаемость плотных газов и способность жидких и твердых тел сопротивляться сжатию указывает на то, что между молекулами действуют также и силы отталкивания.