Лекция 1 введение
 Скачать 0.83 Mb. Скачать 0.83 Mb.
|
Лекция 8Элементы релятивистской механикиПостулаты специальной (частной) теории относительности. Классическая механика прекрасно описывает движение макротел, движущихся с малыми скоростями. Однако в конце 19 века выяснилось, что ее выводы противоречат некоторым опытным данным. В частности, при изучении движения быстрых заряженных частиц оказалось, что оно не подчиняется законам классической механики. Возникли затруднения при попытке применить механику Ньютона к объяснению распространения света. Опыты показали, что скорость света остается одинаковой и независимой от скорости источника света и скорости приемника света. То есть скорость света оказалась одна и та же в двух инерциальных системах отсчета, одна из которых покоится, а другая движется относительно первой. Это противоречило правилу сложения скоростей классической механики. Одновременно было показано противоречие между классической теорией и уравнениями Максвелла, лежащими в основе понимания света как электромагнитной волны. Необходимо было создать новую механику, которая объяснила бы эти факты, но содержала бы и классическую механику, как предельный случай малых скоростей. Это удалось сделать А.Эйнштейну, который заложил основы специальной теории относительности. Эта теория представляет собой современную физическую теорию пространства и времени. В основе теории лежат постулаты Эйнштейна, сформулированные им в 1905 г. и вытекающие из экспериментов. І. Принцип относительности: Никакие опыты, проведенные внутри данной инерциальной системы отсчета, не дают возможности обнаружить, покоится ли данная система или движется прямолинейно и равномерно. То есть все законы природы (а не только законы механики) инвариантны по отношению к переходу от одной инерциальной системы отсчета к другой. ІІ. Принцип инвариантности скорости света: скорость света в вакууме не зависит от скорости движения источника света или приемника (наблюдателя) и одинакова во всех инерциальных системах отсчета. Согласно второму постулату, постоянство скорости света – фундаментальное свойство природы. Преобразования Лоренца. 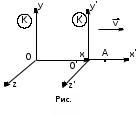 Исходя из этих принципов Эйнштейн, получил ряд необычных выводов, в частности о том, что время в разных инерциальных системах течет неодинаково. Эйнштейн показал, что для выполнения принципов необходимо преобразования Галилея заменить преобразованиями Лоренца. Рассмотрим две инерциальные системы отсчета: К(x,y,z) и K’(x’,y’,z’), движущуюся относительно К поступательно в направлении оси х с постоянной скоростью v (рис.). Преобразования, полученные впервые Лоренцом, имеют вид (здесь = v/c < 1): При переходе от K’→К: 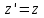 , , 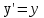 , , 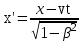 , , 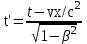 ; ; При переходе K →К’: 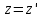 , , 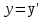 , , 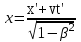 , , 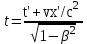 . .Видно, что относительно перемены системы отсчета преобразования симметричны и отличаются лишь знаком при v. Это очевидно, т.к. если скорость движения К’ относительно К равна v, то скорость К относительно К’ равна –v. Следствия из преобразований Лоренца.Из преобразований Лоренца вытекает важный вывод о том, что и расстояние, и промежуток времени между двумя событиями меняются при переходе к другой инерциальной системе отсчета. В закон преобразования координат входит время, а в закон преобразования времени – координаты, т.е. устанавливается связь пространства и времени. Рассмотрим подробнее ряд следствий из преобразований Лоренца. 1. Одновременность событий в разных системах отсчета. Рассмотрим ситуацию, когда в точках с координатами х1 и х2 в системе отсчета К(x,y,z) в моменты времени t 1 и t2 - происходят какие либо два события, промежуток времени между событиями обозначим t (t2 - t 1 = t). Тогда, согласно преобразованиям Лоренца, в системе отсчета K’(x’,y’,z’) промежуток времени и расстояние между этими событиями будут равны 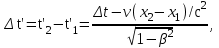 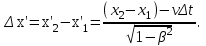 Отсюда видно, что если в системе К два события происходят в одной точке (х=0) и являются одновременными (t=0), то они являются одновременными и пространственно совпадающими (t’=0, x’=0) в любой инерциальной системе отсчета. Но из этих же уравнений следует, что если события в системе К одновременны (t=0), но пространственно разобщены (х = х2 - х1 ≠ 0), то в системе K’ они произойдут не одновременно (t’ = t’2 ‑ t’1 ≠ 0). Следовательно, понятие одновременности относительно. 2. Длина тел в разных системах отсчета. Рассмотрим стержень, расположенный вдоль оси x’ и покоящийся относительно системы K’. Длина стержня в этой системе будет l0’=x’2 - x’1. Определим длину этого стержня в системе К, относительно которой он движется со скоростью v. Для этого необходимо измерить координаты его концов x2 и x1 в один и тот же момент времени (т.е. t=0). Их разность l = x2 - x1 и будет искомой длиной в системе К. Используя преобразования Лоренца, можно получить: 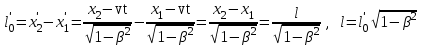 . .Из полученного выражения следует, что l0’ › l. Таким образом, длина стержня, измеренная в системе, относительно которой стержень движется, оказывается меньше длины, измеренной в системе, относительно которой он покоится. Так называемое Лоренцево сокращение длины тем больше, чем больше скорость движения. Поперечные размеры тела не зависят от скорости движения и одинаковы во всех инерциальных системах отсчета. Это подтверждается экспериментально при наблюдении эффекта торможения пучков элементарных частиц в земной атмосфере. 3. Длительность событий в двух разных системах отсчета. Пусть в некоторой точке х’, покоящейся относительно К’, происходит событие, длительность которого (т.е. разность показаний часов в начале и конце события) t’2 – t’1 = τ’. Найдем длительность этого же события t2 - t1 = τ в системе К . В данном случае нужно применить преобразования Лоренца для перехода из K’ → К, так как данные преобразования времени содержат не изменяющуюся координату х’ (часы покоятся в K’ и поэтому x’=0). Согласно преобразованиям Лоренца в данном случае имеем 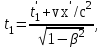 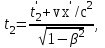 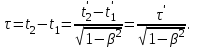 Интервал времени между двумя событиями, отсчитанный в системе координат, относительно которой часы покоятся, называется собственным временем и обозначается τ0, то есть τ’ = τ0. |
