Лекция 1 введение
 Скачать 0.83 Mb. Скачать 0.83 Mb.
|
 Рис. 1 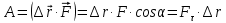 где Fτ - касательная составляющая силы, т.е. проекция 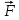 на направление вектора на направление вектора 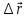 . Если же сила меняется по величине и по направлению или перемещение не прямолинейно, то траекторию движения разбивают на малые участки dr - так, чтобы участок можно было бы считать прямолинейным и силу, действующую на нем - постоянной. Тогда работа на этом участке: . Если же сила меняется по величине и по направлению или перемещение не прямолинейно, то траекторию движения разбивают на малые участки dr - так, чтобы участок можно было бы считать прямолинейным и силу, действующую на нем - постоянной. Тогда работа на этом участке: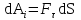 а работа на всем пути равна сумме всех элементарных работ: 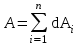 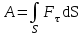 Для вычисления такого интеграла надо знать зависимость Fτ от S. Если эту зависимость представить графически (рис.2), тогда работа силы по перемещению из S1 в S2 численно равна площади заштрихованной фигуры, ограниченной кривой F(S), координатной осью S и двумя вертикальными прямыми S1 и S2. 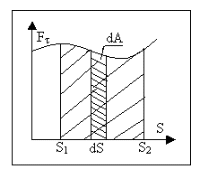 Рис.2 Сила не совершает работу (А=0), если r=0 или угол между направлением силы и вектором перемещения α = π/2. Если π/2, то А0; если π/2 , то А0. При одновременном действии на тело нескольких сил, работа равна алгебраической сумме работ составляющих сил 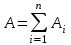 . .Для характеристики скорости совершения работы вводится понятие мощности. Мощностью, развиваемой силой  , называется скалярная физическая величина, численно равная работе, совершаемой этой силой за единицу времени: , называется скалярная физическая величина, численно равная работе, совершаемой этой силой за единицу времени: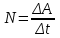 . .Если в разные моменты времени dt совершаются разные работы, то используют понятие мгновенной мощности:  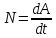 Для движущихся тел можно получить формулу мгновенной мощности: 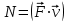 , ,т.е. мощность равна скалярному произведению векторов силы и скорости. Важное требование, предъявляемое к любому двигателю - это способность совершать большую работу за единицу времени, т.е. иметь большую мощность. Из полученной формулы следует, что для достижения этой цели необходимо либо увеличить силу тяги, развиваемую двигателем (например, автомобиля), либо увеличить его быстроходность. Первый путь связан с увеличением силовых нагрузок на все движущиеся части двигателя, а они имеют ограниченную прочность. Чтобы детали смогли выдерживать действие больших нагрузок, нужно увеличивать их размеры, делать их более массивными. Поэтому все мощные тихоходные машины необычайно громоздкие. Второй путь позволяет получить большие мощности при малых силовых нагрузках на детали двигателя и меньших его размерах. В современное время этот путь наиболее перспективен. Кинетическая и потенциальная энергии Полная механическая энергия Ем складывается из кинетической Ек и потенциальной Еп энергии: Ем = Ек + Еп . Кинетическая энергия Ек – это энергия движущегося тела, она равна работе, которую могло бы совершать тело при торможении до полной остановки: Ек=Атор. Соответственно, эта работа численно равна работе внешней силы по увеличению скорости тела от 0 до 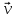 т.е. Ек= Аразгона. Рассчитаем эту работу, учитывая, что работа внешней силы т.е. Ек= Аразгона. Рассчитаем эту работу, учитывая, что работа внешней силы 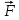 над телом на малом участке перемещения над телом на малом участке перемещения  равна: равна: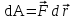 С учетом того, что 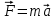 , , 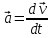 , и , и 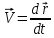 , получаем: , получаем: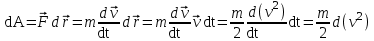 . . Тогда по определению: 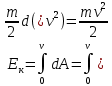 Если система состоит из n движущихся точек, то ее полная кинетическая энергия равна сумме кинетических энергий всех тел. Скорость тел зависит от выбора системы осчета, следовательно кинетическая энергия также является величиной относительной. Кроме контактных взаимодействий существуют без контактные, осуществляемые посредством физических полей. Сила, работа которой по перемещению тела из одной точки пространства в другую точку пространства не зависит от траектории, называется консервативной. Силы, неудовлетворяющие этому условию, называют неконсервативными или диссипативными. Примером таких сил служит сила трения. Работа консервативных сил по изменению конфигурации системы полностью определяется начальной и конечной конфигурациями и ее можно выразить в следующем виде:  . .где Еп – некоторая функция состояния системы, зависящая только от координат всех точек системы. Эту функцию называют потенциальной энергией системы. 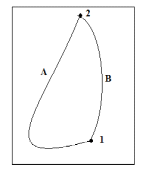 Рис. 3 На рис.3 изображены две различные траектории движения тела под действием некоторой консервативной силы. Работа, совершаемая данной силой на пути 1А2 равна А1А2. Работа, совершаемая на пути 2В1, будет отрицательной и А1А2 = - А2В1. Поскольку совершаемая работа не зависит от формы траектории, мы можем записать: А1А2 +А2В1 ≡0, или:  , ,Из формулы видно, что работа консервативной силы по замкнутому контуру равна нулю. Потенциальная энергия - величина, зависящая от выбора начального положения, при котором Еп=0, т.е. она величина относительная. Конкретный вид зависимости Еп от расположения тел системы связан с характером сил взаимодействия тел. Рассмотрим два примера: 1). Определим Еп тела, поднятого над землей т.е. энергию взаимодействия этого тела с планетой Земля. Известно, что на тело действует консервативная сила тяжести, при небольших высотах h она мало меняется и считается по формуле P = mg. При падении тела сила тяжести совершает работу A=mgh, при этом потенциальная энергия тела уменьшается ровно на эту величину. Если Еп1- потенциальная энергия тела, поднятого над землей, а Еп2 - потенциальная энергия тела на поверхности земли, которую принято считать равной нулю, то из связи работы и изменения энергии, получим: En =mgh. График зависимости Еп от h представлен на рис.4. Ясно, что Еп10 при h0, т.е. над землей и Еп20 при h0, т.е. ниже уровня земли 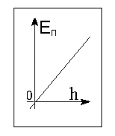 Рис. 4 2) Определим потенциальную энергию упруго деформированной пружины. Из экспериментов известно, что при сжатии (растяжении) пружины в ней возникает сила упругости Fупр = -kx. Знак минус показывает, что сила упругости направлена в сторону противоположную деформации. Работа против этой силы затрачивается на увеличение потенциальной энергии пружины: 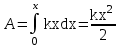 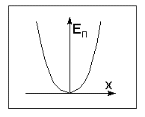 Рис. 5 Еп недеформированной пружины считается равной нулю. Следовательно: 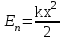 Связь потенциальной энергии тела и действующей на него консервативной силы Рассмотрим движение тела только вдоль направления х: Так как работа консервативной силы равна убыли потенциальной энергии, то dAх= - dEnх или -dEnх = Fx dx, или через частные производные: 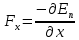 , ,По аналогии для направлений y, z: 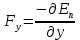 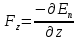 ; ;но 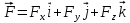 , отсюда: , отсюда: 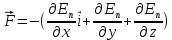 Введем понятие градиента некоторой скалярной величины А: . 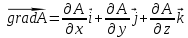 , ,тогда 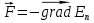 .Закон сохранения и превращения энергии в механике. Закон сохранения и превращения энергии был сформулирован Майером и.Гельмгольцем. В замкнутой системе энергия может переходить из одних видов в другие и передаваться от одного тела другому, но общее количество энергии остается неизменным. В природе и технике постоянно имеют место превращения одних видов энергии в другие. Например, в электродвигателях электрическая энергия переходит в механическую, в ядерном реакторе ядерная энергия переходит в тепловую, затем в механическую и электромагнитную, при фотоэффекте - электромагнитная в электрическую и т.д. Закон сохранения и взаимопревращения энергии является одним из фундаментальных законов природы. Если в замкнутой системе тел действуют консервативные силы, а внешние силы – стационарны и консервативны, то такая система называется консервативной. Для такой системы механическая энергия не переходит в другие виды и остается постоянной во времени (при этом возможен переход потенциальной энергии в кинетическую и наоборот) Е= Ек + Еп =const . Лекция 5. Динамика вращательного движения Момент инерции материальной точки относительно некоторой оси есть скалярная физическая величина равная произведению массы этой точки на квадрат кратчайшего расстояния от нее до оси вращения: Iмат т 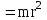 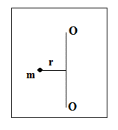 Рис. 1 Любое твердое тело можно представить как бесконечное множество материальных точек. Тогда момент инерции твердого тела равен: Iтв тела =  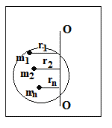 Рис. 2 При непрерывном распределении масс тела эта сумма сводится к интегралу:   , ,где r – кратчайшее расстояние от точки до оси вращения. На основании этой формулы рассчитываются моменты инерции тел различной формы. Например: 1) полый тонкостенный цилиндр или обруч радиуса R, массой m и осью вращения, совпадающей с осью симметрии 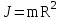 ; ; 2) сплошной цилиндр или диск радиуса R, массой m и осью вращения, совпадающей с осью симметрии 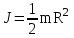 ; ; 3) шар радиуса R, массой m и осью вращения, проходящей через его центр 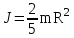 . . Приведенные примеры показывают, что момент инерции тела зависит от его массы, формы, геометрических размеров, его расположения относительно оси вращения, распределения массы по объему тела. Расчет моментов инерции тел относительно осей, не совпадающих с осью симметрии более сложен. В таких случаях применяется теорема Штейнера: момент инерции любого тела относительно произвольной оси ОО равен сумме момента инерции этого тела JO относительно оси АА , параллельной данной и проходящей через центр масс тела С, и произведения массы тела на квадрат расстояния между осями: (рис. 6.) 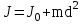 . .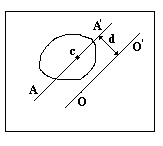 Рис. 3. Моментом силы 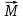 относительно неподвижной точки О называется векторная физическая величина, равная векторному произведению радиуса-вектора относительно неподвижной точки О называется векторная физическая величина, равная векторному произведению радиуса-вектора 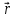 , проведенного из точки О в точку приложения силы (на рисунке точка А), на вектор силы: , проведенного из точки О в точку приложения силы (на рисунке точка А), на вектор силы: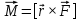  Рис. 4. Направление вектора 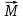 перпендикулярно плоскости, в которой лежат вектора перпендикулярно плоскости, в которой лежат вектора 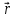 и и 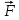 . Его направление совпадает с направлением поступательного движения правого винта при его вращении от . Его направление совпадает с направлением поступательного движения правого винта при его вращении от 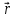 к к 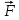 (рис.4.). (рис.4.).Модуль момента силы: M=F∙r sinα =F∙l , где l - плечо силы - кратчайшее расстояние между линией действия силы и точкой О. Если к точке А приложено несколько сил, то результирующий момент сил будет равен векторной сумме моментов всех сил:  Момент силы, действующей на тело относительно неподвижной оси z, есть скалярная величина Mz, равная проекции на эту ось вектора момента силы, определенного относительно произвольной точки О данной оси z (рис.5.) 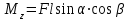 . .Значение момента Mz не зависит от положения точки О на оси z.  Рис. 5. При заданном 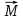 величина и направление Mz зависят от выбора оси z. Это выражение можно сделать более наглядным. Для этого представим радиус-вектор величина и направление Mz зависят от выбора оси z. Это выражение можно сделать более наглядным. Для этого представим радиус-вектор 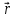 в виде суммы двух составляющих: rz – параллельной оси z и R- перпендикулярной к оси. в виде суммы двух составляющих: rz – параллельной оси z и R- перпендикулярной к оси.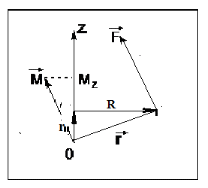 Рис. 6 Тогда: 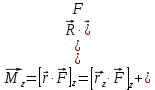 Первое слагаемое перпендикулярно оси z как результат векторного произведения и не может давать вклад в проекцию момента силы на ось z, поэтому остается: 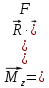 Здесь 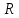 - плечо силы - плечо силы 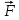 относительно оси z. относительно оси z.Теперь представим 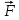 как сумму трех составляющих: параллельной оси z как сумму трех составляющих: параллельной оси z 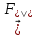 , параллельной вектору , параллельной вектору 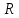 - -  и тангенциальной составляющей силы и тангенциальной составляющей силы 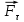 (если представить окружность радиуса (если представить окружность радиуса 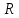 в плоскости перпендикулярной оси z, то составляющая в плоскости перпендикулярной оси z, то составляющая 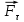 направлена по касательной к окружности). направлена по касательной к окружности). 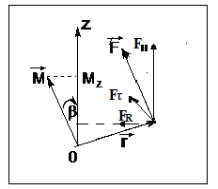 Рис. 7. Тогда: 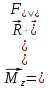 Но вектор 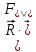 перпендикулярен оси z, следовательно его проекция на ось равна 0, векторы перпендикулярен оси z, следовательно его проекция на ось равна 0, векторы 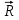 и и  коллинеарны (параллельны друг другу), следовательно их векторное произведение равно нулю коллинеарны (параллельны друг другу), следовательно их векторное произведение равно нулю  , тогда: , тогда: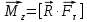 . .Очевидно, что момент 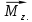 характеризует способность силы характеризует способность силы 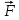 не сдвинуть тело поступательно, а повернуть тело вокруг оси z. Рассматриваемый поворот может быть вызван только тангенциальной составляющей силы не сдвинуть тело поступательно, а повернуть тело вокруг оси z. Рассматриваемый поворот может быть вызван только тангенциальной составляющей силы 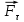 и поворот будет тем больше, чем больше плечо силы и поворот будет тем больше, чем больше плечо силы 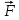 . .Момент импульса (количества движения) материальной точки А относительно неподвижной точки О есть векторная физическая величина, определяемая векторным произведением двух векторов: радиуса-вектора 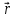 , проведенного из точки О в точку А, и импульса материальной точки , проведенного из точки О в точку А, и импульса материальной точки 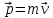 : :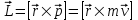 . .Направление вектора  совпадает с направлением поступательного движения правого винта при его вращении от совпадает с направлением поступательного движения правого винта при его вращении от 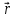 к к  (рис.8.). (рис.8.).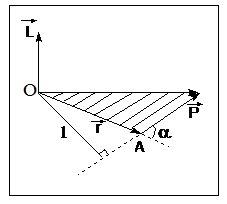 Рис. 8. Модуль вектора: 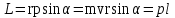 , ,где - угол между векторами 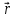 и и  , l - плечо вектора , l - плечо вектора  относительно точки О. относительно точки О.Моментом импульса точки относительно неподвижной оси z называется скалярная величина Lz, равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки О данной оси. Момент импульса системы материальных точек есть векторная сумма моментов импульса всех точек системы. Если число точек системы равно n, тогда: 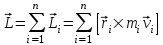 Можно показать, что скорость изменения момента импульса системы материальных точек относительно неподвижной точки равна результирующему моменту относительно той же точки всех внешних сил, действующих на систему. 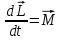 ( 1 ) ( 1 )Уравнение (1) есть основной закон вращательного движения системы материальных точек относительно некоторой неподвижной точки О. Взяв от векторов, стоящих в левой и правой частях уравнения ( 1 ), их проекции на ось z, получим: 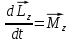 ( 2) ( 2) Ранее мы говорили о том, что любое твердое тело можно представить как систему материальных точек. Тогда, если тело закреплено в двух точках, так что может вращаться вокруг неподвижной оси z, проходящей через эти точки, то уравнение (2) есть основной закон динамики вращательного движения твердого тела вокруг неподвижной оси. Скорость изменения момента импульса тела относительно неподвижной оси вращения равна результирующему моменту относительно этой оси всех внешних сил, действующих на тело. Это выражение сходно с основным законом динамики поступательного движения 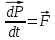 . .Найдем выражение для момента импульса Lz твердого тела. При вращательном движении твердого тела вокруг неподвижной оси угловые скорости всех его точек равны. 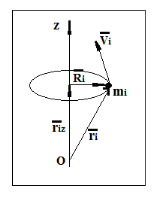 Рис. 9. Для i – ой материальной точки 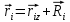 , где Ri – радиус окружности, по которой движется точка. Можно доказать, что: , где Ri – радиус окружности, по которой движется точка. Можно доказать, что: 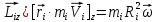 И для твердого тела:  Момент импульса твердого тела относительно неподвижной оси z равен произведению момента инерции этого тела относительно той же оси на угловую скорость вращения тела вокруг этой оси. Из последней формулы следует, что основное уравнение динамики для тела, вращающегося вокруг неподвижной оси z можно представить в виде:  Если тело абсолютно твердое, то его момент инерции не зависит от времени, тогда:  и и 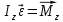 или: или: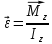 Следовательно, момент инерции тела является таким свойством тела, как мера инертности во вращательном движении вокруг неподвижной оси. По форме оно сходно с уравнением II закона Ньютона. Из их сопоставления вытекает, что при вращательном движении роль массы играет момент инерции, роль линейного ускорения - угловое ускорение, роль силы - момент силы. Закон сохранения момента импульса 1. Момент импульса замкнутой системы материальных точек относительно неподвижной точки не меняется с течением времени. 2. Если результирующий момент всех внешних сил, приложенных к системе, относительно какой-либо неподвижной оси тождественно равен нулю, то момент импульса системы относительно той же оси не изменяется с течением времени. Закон сохранения момента импульса вытекает из такого свойства материи, как изотропность пространства. Изотропность пространства означает, что поворот в нем замкнутой системы как целого не должен отражаться на физических свойствах системы и законах ее движения. Работа и кинетическая энергия при вращательном движении твердого тела. При элементарном повороте твердого тела вокруг неподвижной оси на угол dφ работа равна: δА = 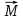 d d При конечном повороте на угол φ: А= 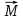  Кинетическая энергия твердого тела, вращающегося вокруг неподвижной оси со скоростью 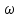 , определяется по формуле: , определяется по формуле: где I - момент инерции тела. Лекция 6 Колебательное движение Основные характеристики гармонического колебания Колебательным движением называется процесс, повторяющийся с течением времени. Если колебания повторяются через один и тот же промежуток времени, то они называются периодическими. Промежуток времени Т, через который процесс полностью повторяется, называется периодом колебания. В зависимости от характера воздействия на колеблющуюся систему различают свободные незатухающие (собственные идеальные) колебания, затухающие колебания, вынужденные колебания, автоколебания. Если колебания описываются по закону синуса или косинуса, то они называются гармоническими.  или или  , ,А - амплитуда колебаний или максимальное смещение из положения равновесия, 0 - круговая (циклическая) частота,  - фаза колебаний в момент времени t, - начальная фаза колебаний или фаза в момент времени t=0. Такие колебания происходят под действием так называемых квазиупругих сил. Квазиупругие силы - это силы, пропорциональные смещению переменной величины. - фаза колебаний в момент времени t, - начальная фаза колебаний или фаза в момент времени t=0. Такие колебания происходят под действием так называемых квазиупругих сил. Квазиупругие силы - это силы, пропорциональные смещению переменной величины.Рассмотрение гармонических колебаний важно по двум причинам: 1) колебания, встречающиеся в природе и технике, часто имеют характер близкий к гармоническим; 2) различные периодические процессы можно представить как сложение нескольких гармонических колебаний. Скорость и ускорение при гармоническом колебании Скорость гармонического колебания есть первая производная от смещения х по времени t. Пусть  , , тогда 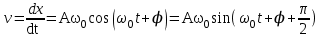 . . Скорость сдвинута по фазе относительно смещения на /2. Максимальное значение скорости равно 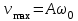 . .Ускорение а гармонического колебания есть первая производная от скорости v по времени t.  Ускорение сдвинуто по фазе относительно смещения на . Максимальное значение модуля ускорения равно  . На рис. представлены графики зависимости х, v и a от времени. Для удобства изображения начальная фаза принята равной нулю =0, т.е. х=0 при t=0. . На рис. представлены графики зависимости х, v и a от времени. Для удобства изображения начальная фаза принята равной нулю =0, т.е. х=0 при t=0.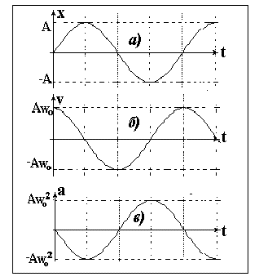 Рис. Зависимость между ускорением и смещением можно получить, если в формуле для ускорения множитель 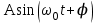 заменить на х, тогда получим заменить на х, тогда получим 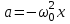 . .Пружинный маятник Рассмотрим колебания шарика массы m, подвешенного на пружинке жесткости к. Составим уравнение динамики гармонических колебаний шарика. По 2 закону Ньютона: 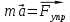 Тогда  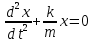 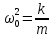   Рис. Полученное выражение называют дифференциальным уравнением гармонических колебаний. Это линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами. Его решениями являются: x=Asin(ω0 t+φ) , x=Acos(ω0 t+φ) . Кинетическая энергия материальной точки при гармоническом колебании равна  Потенциальная энергия материальной точки при гармоническом колебании под действием упругой силы, согласно ее определению, равна 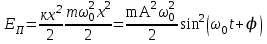 Полная энергия колеблющейся точки 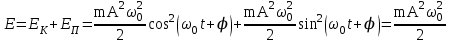 Полная энергия не зависит от времени. Следовательно, при гармонических колебаниях выполняется закон сохранения механической энергии (идеальные колебания без рассеяния энергии). Физический маятник Физический маятник - это твердое тело, совершающее колебания под действием силы тяжести вокруг неподвижной горизонтальной оси, не проходящей через центр тяжести С (рис.). Ось проходит через точку О. Если маятник отклонить от положения равновесия на малый угол и отпустить, он будет совершать колебания. 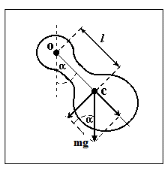 Рис. Согласно основному уравнению динамики вращательного движения твердого тела: 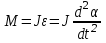 , , где J - момент инерции маятника относительно оси, М ‑ момент силы, возвращающей физический маятник в положение равновесия. Он создается силой тяжести, ее момент равен  . Тогда: . Тогда: 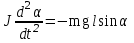 . .Это дифференциальное уравнение колебаний для произвольных углов отклонения. При малых углах, когда 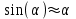 , ,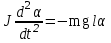 или, принимая или, принимая 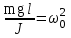 , , получим дифференциальное уравнение колебания физического маятника  . .Его решения имеют вид 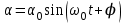 или или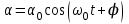 . Таким образом, при малых отклонениях от положения равновесия физический маятник совершает гармонические колебания с циклической частотой . Таким образом, при малых отклонениях от положения равновесия физический маятник совершает гармонические колебания с циклической частотой 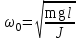 и периодом и периодом 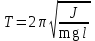 . .Математический маятник - это материальная точка с массой m (тяжелый шарик малых размеров), подвешенная на невесомой (по сравнению с m шарика), упругой, нерастяжимой нити длинною l. Если вывести шарик из положения равновесия, отклонив его от вертикали на небольшой угол , а затем отпустить, он будет совершать колебания. Если рассматривать данную систему как физический маятник с моментом инерции материальной точки J = ml2, то из формул для физического маятника получим выражения для циклической частоты и периода колебаний математического маятника 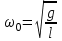 , , 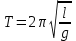 . . Затухающие колебания В рассмотренных примерах гармонических колебаний единственной силой, действующей на материальную точку, была квазиупругая сила F и не учитывались силы сопротивления, которые присутствуют в любой реальной системе. Поэтому рассмотренные колебания можно назвать идеальными незатухающими гармоническими колебаниями. Наличие в реальной колебательной системе силы сопротивления среды приводит к уменьшению энергии системы. Если убыль энергии не пополнять за счет работы внешних сил, колебания будут затухать. Затухающими называются колебания с уменьшающейся во времени амплитудой.  Рис. Рассмотрим свободные затухающие колебания. При небольших скоростях сила сопротивления FC пропорциональна скорости v и направлена против движения: 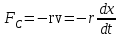 , ,где r - коэффициент сопротивления среды Тогда уравнение затухающих колебаний 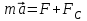 , , 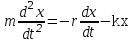 , , 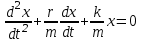 . . Обозначим 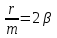 , ,  . . Тогда дифференциальное уравнение приобретает вид: 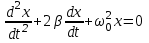 . .Это дифференциальное уравнение затухающих колебаний. Здесь 0 - собственная частота колебаний системы, т.е. частота свободных колебаний при r=0, - коэффициент затухания, который определяет скорость убывания амплитуды. Решениями этого уравнения при условии 0 являются: 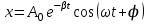 либо либо 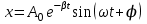 . .График последней функции представлен на рис. Верхняя пунктирная линия дает график функции 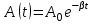 , А0 - амплитуда в начальный момент времени. Амплитуда во времени убывает по экспоненте. , А0 - амплитуда в начальный момент времени. Амплитуда во времени убывает по экспоненте.Введем понятие времени релаксации , как времени, за которое амплитуда уменьшается в e раз:  , ,  , = 1, , = 1, 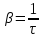 . . Частота и период затухающих колебаний:  , , 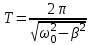 ; ; при очень малом сопротивлении среды (202) период колебаний практически равен 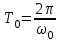 . . С ростом период колебаний увеличивается и при >0 решение дифференциального уравнения показывает, что колебания не совершаются, а происходит монотонное движение системы к положению равновесия. Такое движение называют апериодическим. Для характеристики скорости затухания колебаний служат еще два параметра: декремент затухания D и логарифмический декремент . Декремент затухания показывает, во сколько раз уменьшается амплитуда колебаний за время одного периода Т.  Натуральный логарифм от декремента затухания есть логарифмический декремент 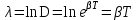 . .Так как 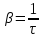 , то , то  , где N - число колебаний за время релаксации , где N - число колебаний за время релаксации  . .Вынужденные колебания. Резонанс. Если на колеблющуюся систему действует периодически изменяющаяся сила, то колебания называются вынужденными. Пусть вынуждающая сила изменяется по гармоническому закону:  . .Дифференциальное уравнение с учетом внешней силы запишется так: 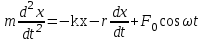 или или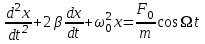 . . Решением неоднородного дифференциального уравнения второго порядка является сумма общего решения однородного уравнения и частного решения неоднородного.  Acos(Ωt + α) Acos(Ωt + α)Поскольку первое слагаемое очень быстро стремится к нулю, то решением будет: х=Acos(Ωt + α) причем Ω - частота вынужденных колебаний, совпадает с частотой колебания вынуждающей силы. Амплитуда вынужденных колебаний - А является сложной функцией от Ω и . 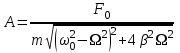 . .Зависимость амплитуды от Ω и представлены на рис. (123). При Ω=0 все кривые сходятся в одной точке оси ординат 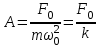 . При различных значениях амплитудные кривые имеют максимумы, которые соответствуют частотам: Ω1 , Ω2 , Ω3 . . При различных значениях амплитудные кривые имеют максимумы, которые соответствуют частотам: Ω1 , Ω2 , Ω3 . Ω 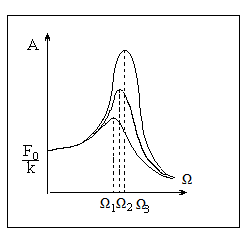 Рис. Явление возрастания, а затем убывания амплитуды колебаний при изменении частоты названо механическим резонансом, а частоты Ω1, Ω2, ... , которым соответствуют максимумы амплитуды, называют резонансными частотами Ωрез. Чтобы определить их значения, необходимо найти максимум для функции амплитуды или, что то же самое, минимум подкоренного выражения (  ). Продифференцировав подкоренное выражение по Ω и приравняв производную нулю (что соответствует минимуму функции А(Ω), получим: ). Продифференцировав подкоренное выражение по Ω и приравняв производную нулю (что соответствует минимуму функции А(Ω), получим: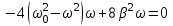 . .Отсюда, резонансная частота Ωрез=  , ,при 0, Ωрез 0. Найдем резонансное значение амплитуды:  . .Другая особенность вынужденных колебаний - это сдвиг фазы, а именно вынужденные колебания отстают по фазе от вынуждающей силы на величину α, для которой 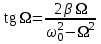 . .Величина сдвига фаз зависит от частоты Ω и коэффициента затухания . Вынужденные колебания и вынуждающая сила имеют одинаковую фазу лишь при =0. При Ω =0 для любых значений сдвиг фазы равен 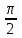 . .Если, например, собственная частота 0 вибраций корпуса корабля или крыльев самолета совпадает с частотой колебаний, возбуждаемых вращательным движением гребного винта или пропеллера, возникнет механический резонанс, который может привести к разрушению. Однако явление резонанса имеет и положительное применение, например, в радиотехнике - для выделения нужного сигнала и множества других, отличающихся по частоте, в акустике - для усиления звучания музыкального инструмента и т.д. Для решения многих технических задач большой интерес представляют автоколебания. Это незатухающие колебания в реальной колебательной системе, осуществляемые под влиянием внешнего переменного воздействия, частота которого равна собственной частоте системы. |
