Лекция 1 введение
 Скачать 0.83 Mb. Скачать 0.83 Mb.
|
 - векторная физическая величина, являющаяся мерой воздействия на тело со стороны других тел или полей, в результате чего тело либо приобретает ускорение, либо деформируется. Взаимодействие тел возможно как при соприкосновении, так и на расстоянии, благодаря силовым полям. В каждый момент времени сила характеризуется числовым значением, направлением в пространстве и точкой приложения. Силы, связанные с перечисленными выше физическими полями, являются первичными, их называют фундаментальными силами. Имеется также множество вторичных сил, которые являются комбинацией фундаментальных сил (в основном – электромагнитные). Например, это силы межатомного и межмолекулярного взаимодействия, силы трения, силы деформации и др. - векторная физическая величина, являющаяся мерой воздействия на тело со стороны других тел или полей, в результате чего тело либо приобретает ускорение, либо деформируется. Взаимодействие тел возможно как при соприкосновении, так и на расстоянии, благодаря силовым полям. В каждый момент времени сила характеризуется числовым значением, направлением в пространстве и точкой приложения. Силы, связанные с перечисленными выше физическими полями, являются первичными, их называют фундаментальными силами. Имеется также множество вторичных сил, которые являются комбинацией фундаментальных сил (в основном – электромагнитные). Например, это силы межатомного и межмолекулярного взаимодействия, силы трения, силы деформации и др.Гравитационное поле – это поле сил взаимодействия (притяжения) тел, имеющих массу. И. Ньютон установил, что для материальных точек формула величины силы гравитации имеет вид  , где G- гравитационная постоянная, m1 и m2 – массы взаимодействующих точек, r- расстояние между ними. , где G- гравитационная постоянная, m1 и m2 – массы взаимодействующих точек, r- расстояние между ними. Электромагнитное поле – это поле сил взаимодействия (притяжения или отталкивания) тел, имеющих электрический заряд. Формулы этих сил будут рассмотрены при изучении электрических и магнитных явлений. Ядерное поле – это поле сил взаимодействия элементарных частиц, из которых состоят атомы и молекулы. Эти силы действуют только на очень малых расстояниях, их свойства рассматриваются при изучении ядер атомов. 2.2. Законы И.Ньютона. Классическая динамика базируется на трех законах Ньютона. Первый закон Ньютона: Тело движется равномерно прямолинейно или находится в состоянии покоя до тех пор, пока другие тела не выведут его из этого состояния. Понятия движения и покоя относительны и зависят от выбора системы отсчета. Свойство тела сохранять состояние покоя или равномерного прямолинейного движения называется инертностью. Первый закон Ньютона называют законом инерции. Система отсчета, в которой он выполняется, считается инерциальной. Любая другая система, движущаяся по отношению к инерциальной с постоянной скоростью, также является инерциальной. Экспериментально установлено, что гелиоцентрическую систему отсчета можно считать инерциальной, а геоцентрическая, строго говоря, не является инерциальной. Однако, для решения многих простых задач и ее считают инерциальной. Второй закон Ньютона. Векторная величина равная произведению массы точки на вектор скорости называется импульсом (количеством движения) точки:  . . Тогда второй закон Ньютона в общем виде будет читаться так: Скорость изменения импульса движущейся материальной точки (тела) равна действующей на нее силе:  Последнюю формулу можно записать в виде 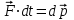 , где , где  - элементарный импульс силы, действующий на точку в течении интервала времени dt, - элементарный импульс силы, действующий на точку в течении интервала времени dt,  - изменение импульса точки за это время. - изменение импульса точки за это время.Если на точку (тело) действует постоянная сила  , то из предыдущей формулы имеем: , то из предыдущей формулы имеем: Умножим обе части равенства на dt 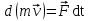 и интегрируя обе части равенства, получим и интегрируя обе части равенства, получим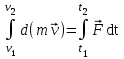 , ,  . . Изменение импульса тела под действием постоянной силы равно произведению этой силы на время ее действия или импульсу силы. Кроме общей формулировки II закона Ньютона часто используют формулировку для случая, когда масса не меняется со временем. Учитывая, что 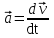 , второй закон Ньютона можно записать в виде: , второй закон Ньютона можно записать в виде: или или 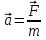 . .Ускорение, приобретаемое телом с постоянной массой под действием силы, прямо пропорционально этой силе, совпадает с ней по направлению и обратно пропорционально массе тела. С математической точки зрения первый закон Ньютона представляет частный случай второго закона Ньютона, так как если результирующая сила равна нулю, то:  =0, то =0, то  =0, =0,  =0 и =0 и 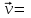 const или const или 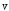 =0. =0.Большое значение в механике имеет принцип независимости действия сил: если на точку (тело) действует одновременно несколько сил, то каждая из них сообщает точке свое ускорение, независимо от других сил. Результирующее ускорение равно векторной сумме ускорений. Для n действующих сил, это записывается в следующем виде: 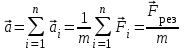 , ,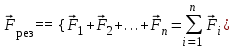 . .Результирующая сила  равна векторной сумме сил, действующих на тело. В этом заключается принцип суперпозиции или принцип независимости действия сил. равна векторной сумме сил, действующих на тело. В этом заключается принцип суперпозиции или принцип независимости действия сил.Третий закон Ньютона. Действия двух тел друг на друга всегда равны по величине и напрвлены по одной прямой, но в противоположных направлениях.  Принцип относительности Галилея Выберем систему отсчета К, связанную с землей. Пусть система К’ движется относительно системы К со скоростью  , направленной вдоль оси Х. Такой выбор облегчает математический расчет, хотя К’ может двигаться произвольно. , направленной вдоль оси Х. Такой выбор облегчает математический расчет, хотя К’ может двигаться произвольно.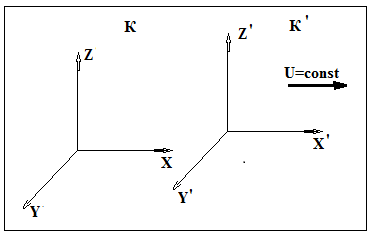 Рис. Представим некоторую точку А и определим ее координаты в сисиеме К как: X,Y, Z а сисиеме К’ как: X’,Y’, Z’. Тогда: 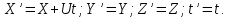 (1) (1)Эти выражения называют преобразованиями Галилея. Они справедливы при движении со скоростями V<<с. В этих случаях неизменно и время, поэтому t’=t. Продифференцируем первые три уравнения по времени:  (2) (2) 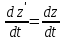 Или:  (3) (3) ; ; 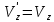 Последние три выражения есть закон сложения скоростей в классической механике. Если взять производные от уравнений (3), получим соотношения для ускорений:  ; ; 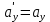 ; ;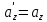 или  . .Отсюда: 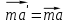 , ,  . (4) . (4)Соотношение (4) показывает, что 2закон Ньютона не изменяется при переходе от одной инерциальной системы отсчета к другой. Первый и третий законы Ньютона являются следствием второго закона, поэтому : Законы динамики Ньютоны инвариантны к преобразованиям Галилея. Это есть принцип относительности Галилея. Примеры сил. 1) Закон всемирного тяготения. Все тела притягиваются друг к другу:  ; ;2) Сила тяжести: F=mg, где для Земли g=G  . .3) Вес тела – это сила, с которой тело действует на опору или нить подвеса. 4) Сила упругости: F=kx, или закон Гука: каково удлинение, такова и сила. 5) Сила трения: скольжения, качения, покоя. Лекция 3 Закон сохранения импульса. Рассмотрим систему n взаимодействующих материальных точек. На каждую точку действуют внутренние и внешние силы. Силы взаимодействия между телами системы называются внутренними, а силы, которые действуют со стороны тел, не входящих в рассматриваемую систему, называются внешними. Массы точек - m1, m2, ..., mn, , их координаты: r1, r2, …..rn. скорости их движения - v1, v2,...,vn. Пусть 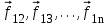 - внутренние силы, действующие на первую точку со стороны второй, третьей и т.д. - внутренние силы, действующие на первую точку со стороны второй, третьей и т.д. 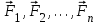 - внешние силы, действующие на первую, вторую и т.д. материальные точки. - внешние силы, действующие на первую, вторую и т.д. материальные точки. Так как внутренние силы являются силами взаимодействия между телами, то они должны подчиняться третьему закону Ньютона  . . Центр масс. Закон движения центра масс. Центр масс (или центр инерции) системы материальных точек есть некоторая точка в пространстве С, положение которой характеризует распределение масс системы. 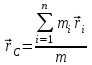 , ,где n – число точек системы, m1, m2…mn – их массы;  - их радиусы-векторы; m – общая масса системы. - их радиусы-векторы; m – общая масса системы.Скорость центра масс:  . .Так как 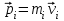 , , 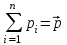 - импульс всей системы, то - импульс всей системы, то  или илиимпульс системы  равен сумме импульсов всех точек системы или равен произведению массы системы на скорость ее центра масс. равен сумме импульсов всех точек системы или равен произведению массы системы на скорость ее центра масс.Замкнутая система материальных точек. Запишем II закон Ньютона для каждой точки: 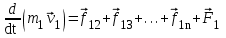  . . . . . . 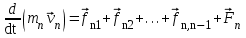 . .Если просуммировать эти уравнения по всем точкам и учесть, что при двойном суммировании внутренних сил, согласно третьему закону Ньютон, сумма внутренних сил равна нулю (рис. ), то  Рис.  , и , и 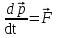 , где , где 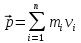 , ,  . .Система называется замкнутой, если. на нее не действуют внешние силы, или их сумма равна нулю, то есть 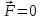 , тогда , тогда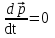 , , 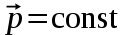 . .Это выражение является законом сохранения импульса. Суммарный импульс замкнутой системы точек (тел) не меняется с течением времени. Закон сохранения импульса является следствием такого свойства пространства, как однородность. Однородность пространства означает, что параллельный перенос в нем замкнутой системы как целого не должно отражаться на физических свойствах системы и законах ее движения. Закон сохранения импульса находит широкое применение в природе и технике. Примером может служить явление отдачи ружья при выстреле пули. Закон движения центра масс По II закону Ньютона  . Отсюда . Отсюда 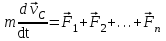 , т.е. центр масс системы движется как материальная точка, в которой сосредоточена масса всей системы и на нее действует сила, равная геометрической сумме всех внешних сил, действующих на тела системы. Это есть закон движения центра масс. Если система замкнута, то , т.е. центр масс системы движется как материальная точка, в которой сосредоточена масса всей системы и на нее действует сила, равная геометрической сумме всех внешних сил, действующих на тела системы. Это есть закон движения центра масс. Если система замкнута, то 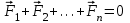 , ,  и и  Принцип реактивного движения. Уравнение движения тела с переменной массой. Особый интерес представляет применение закона сохранения импульса к явлению «непрерывной отдачи», происходящему в реактивном двигателе (ракете). Если рассматривать ракету и выбрасываемые ею продукты сгорания как единую механическую систему, то для получения уравнения ее движения можно применить закон сохранения импульса. Эта идея была развита в трудах Циолковского. Уравнение движения тела с переменной массой было выведено Мещерским. При выводе уравнения необходимо учитывать, что в процессе движения ракеты изменяется ее масса, т.к. удаляются продукты сгорания. Пусть в момент времени t масса ракеты – m и ее скорость - 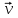 . Через интервал времени dt масса ее уменьшится на dm и станет равной m-dm, а скорость будет равна . Через интервал времени dt масса ее уменьшится на dm и станет равной m-dm, а скорость будет равна . Образовавшиеся продукты сгорания топлива за время dt приобрели импульс . Образовавшиеся продукты сгорания топлива за время dt приобрели импульс  , где , где 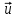 - скорость истечения газа относительно ракеты. Изменение импульса всей системы (ракета + продукты сгорания) за время dt равно - скорость истечения газа относительно ракеты. Изменение импульса всей системы (ракета + продукты сгорания) за время dt равно (1) (1)Так как  - пренебрежимо малая величина, поэтому после сокращений получим - пренебрежимо малая величина, поэтому после сокращений получим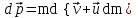 . Полагая, что на ракету в далеком космосе не действуют внешние силы, то из закона сохранения импульса следует, что: . Полагая, что на ракету в далеком космосе не действуют внешние силы, то из закона сохранения импульса следует, что: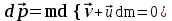 . .Разделим обе части равенства на dt и после простых преобразований получим 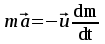 . .Выражение в правой части равенства  имеет размерность силы и называется реактивной силой имеет размерность силы и называется реактивной силой 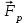 . .Таким образом, уравнение динамики движения ракеты в космосе можно записать в виде:  . . Если на систему действуют внешние силы  , то , то 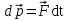 и аналогичным образом получается уравнение Мещерского в виде : и аналогичным образом получается уравнение Мещерского в виде :  Лекция 4. Энергия, работа, мощность. Единой мерой различных форм движения и взаимодействия всех видов материи является энергия. Различным видам движения материи, соответствуют различные виды энергии: механическая, тепловая, химическая, электромагнитная, атомная. Простейшей форме движения – механической, соответствует механическая энергия. Например, катящийся шар, сталкиваясь с некоторым телом, перемещает его, т.е. совершает работу. Растянутая пружина, сокращаясь после устранения деформирующей силы, совершает работу по перемещению своих частей (витков). Следовательно, катящийся шар и растянутая пружина обладают механической энергией. Процесс изменения механической энергии тела под действием силы называется процессом совершения работы. Приращение энергии тела в этом процессе называется работой силы, отсюда следует общее соотношение, связывающее работу и изменение энергии А=Е2-Е1, где: А – совершаемая работа, Е1 и Е2 - энергии системы в начальном и конечном состояниях. Сила, приложенная к телу, совершает работу, если тело перемещается. Если тело движется прямолинейно и на него действует постоянная сила, направленная под углом к перемещению, то работа равна скалярному произведению векторов перемещения и силы (рис. 1) |
