Конспект лекций (wecompress.com). Лекция основные понятия и определения
 Скачать 5.8 Mb. Скачать 5.8 Mb.
|
|
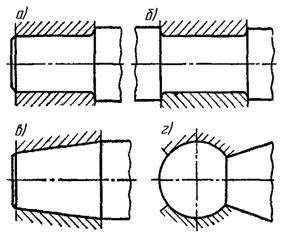
Степень точности зубчатых передач При изготовлении колёс неизбежны погрешности, выражающиеся в радиальном биении зубчатого венца, отклонениях шага и профиля зуба, соосности осей колёс и пр. Эти погрешности влекут появление шума, вибраций, динамическим нагрузкам при работе. В связи с этим, точность передач регламентируют стандартом, предусматривающим 12 степеней точности в порядке её убывания. На выбор степени точности колеса, которое мы хотим изготовить влияют: 1) Нагруженность передачи; 2) Скорость вращения колеса; 3) Экономические возможности. Связь перечисленных параметров регламентируется справочной литературой. 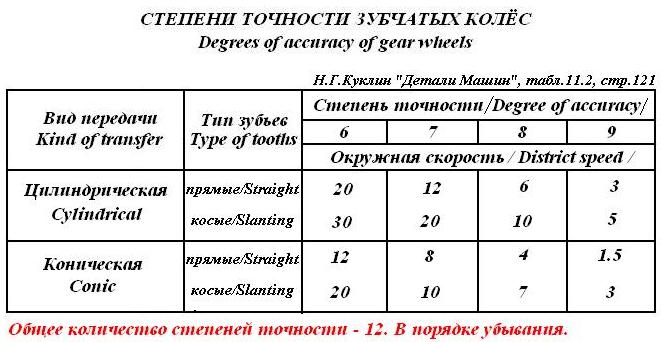 Основные параметры зубчатых колёс При подборе зубчатого колеса взамен изношенного, опираются на характеристики, которые могут быть выбиты на боковой поверхности зубчатого венца: 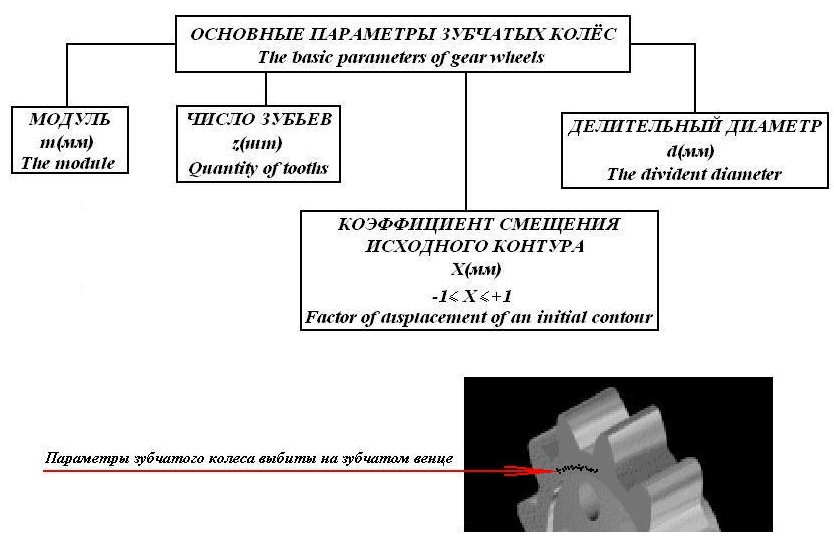 Конструкция зубчатых колёс Определяется условиями их работы и габаритами. Так, колёса ø до 150мм получают в форме сплошных дисков из проката или поковок. Колёса ø св.500 мм получают ковкой, отливкой, сваркой. Колёса ø св.500 мм делают отливкой или сваркой. В целях экономии легированных сталей крупные колёса выполняют сборными. 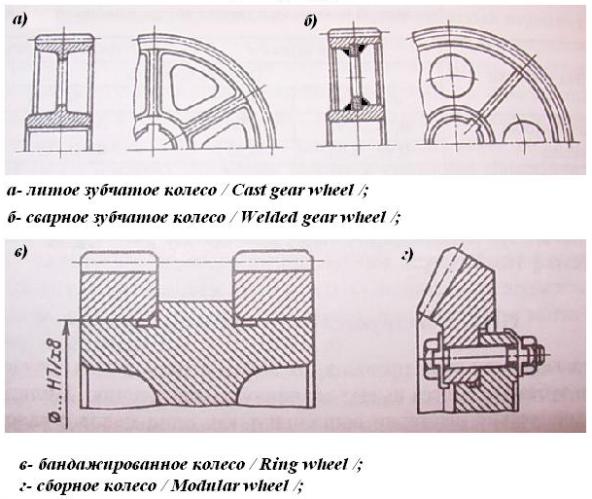 Основная геометрия цилиндрической зубчатой передачи 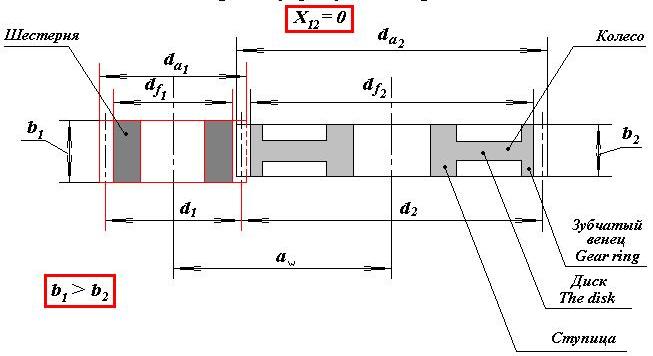 d - делительный (средний) диаметр зубчатого колеса; dа- диаметр окружности вершин зубьев; df - диаметр окружности впадин зубьев; b - ширина зубчатого венца. Простейшие формульные зависимости для определения размеров зубчатой передачи: 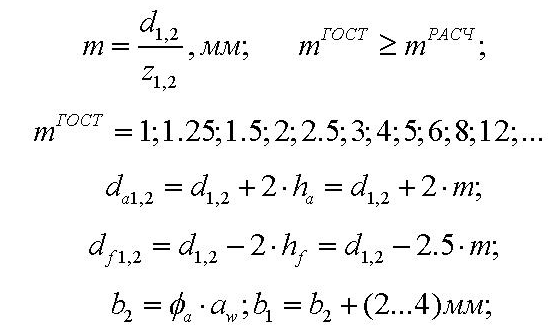 Модуль m определяют в ходе предварительного расчёта и полученное значение округляют до стандартного: mгост>mрасч. Стандартные ряды модулей приведены в справочной литературе. Число зубьев z1 и z2 связаны соотношением с передаточным числом зубчатой передачи. При проектировочном расчёте задаются числом зубьев шестерни z1 = 18…22, опираясь на которое определяют число зубьев колеса z2. ha- высота головки зуба; hf- высота ножки зуба. аw – межосевое расстояние - основной параметр зубчатой передачи, мм: 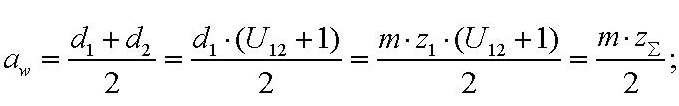 где z∑ - суммарное число зубьев колёс 1 и 2 : z∑ = z1+ z2 Угол наклона зубьев косозубой передачи:  Нагрузки в зубчатых передачах и их приведение. При определении нагрузок силы взаимодействия зубьев принято определять в полюсе зацепления Р. 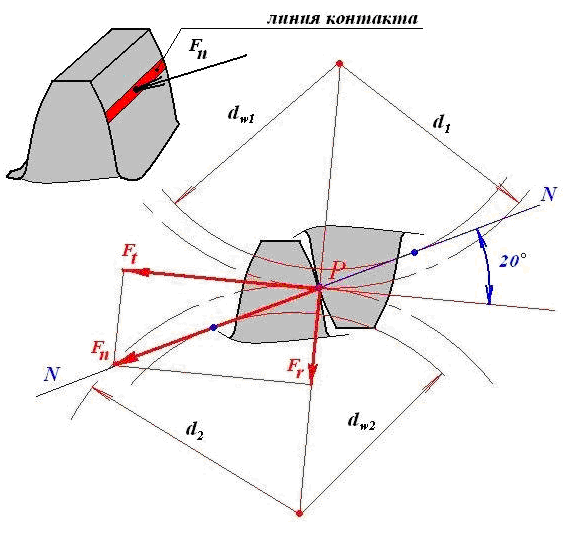 При анализе нагрузки на зуб распределенную по контактной площадке нагрузку заменяют равнодействующей Fп, направленной по линии зацепления N-N, где αw - угол зацепления, определяющийся профилем зуборезного инструмента и стандартно равный 20°. При этом в прямозубых цилиндрических передачах сила Fп , благодаря эвольвентному профилю зубьев, раскладывается на две составляющие: Fr – радиальную силу и Ft - окружную силу. Указанные нагрузки связываются определёнными соотношениями, которые мы приведём чуть ниже. В косозубых передачах, а также червячных и конических, у силы Fп появляется ещё одна составляющая – Fа- осевая сила. 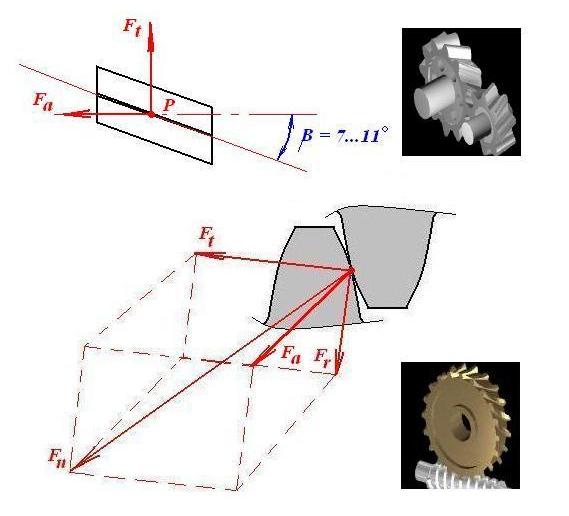 Численные значения сил могут быть определены по простым соотношениям, в частности для цилиндрических прямозубых и косозубых передач: 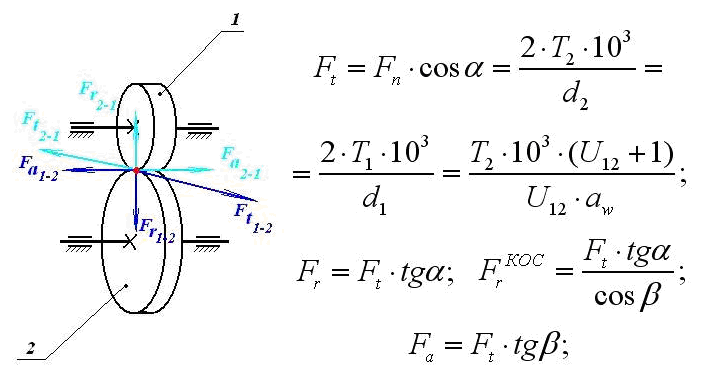 Нагрузки, действующие между зубьями зубчатых колёс, воспринимаются не только самими зубьями, но и передаются на другие детали механизма, в частности на валы зубчатых колёс, их оси и подшипниковые опоры. Поэтому при расчётах валов и осей зубчатых колёс, а также выборе подшипников, возникает необходимость приведения сил в зацеплении к валу (оси) для последующего расчёта изгибающих моментов, действующих на валу (оси). При этом вал рассматривают в двух ортогональных плоскостях, поскольку привести все силы в одной плоскости не представляется возможным из-за их ортогонального расположения. Рассмотрим пример приведения нагрузок ко вторичному валу червячной передачи. Введём две ортогональных плоскости V и Н. Рассмотрим проекции на вал II действующих нагрузок в этих плоскостях: 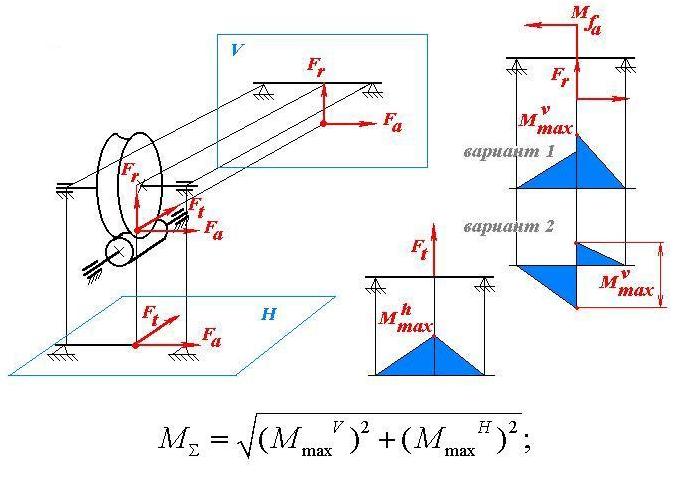 На плоскости «V» действуют силы Fr и Fа, а на плоскости «Н»- только Ft, а сила Fа сонаправлена с валом и не даёт на него изгибающей нагрузки. Приведение силы Fа к валу для плоскости «V» производят через сосредоточенный момент МFа, вычисляемый, как: 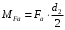 Полученные две расчётные схемы исследуются методами «Сопротивления материалов», в процессе чего находятся максимальные значения изгибающих моментов, действующих на валу II, в обеих рассматриваемых плоскостях: 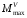 и и 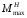 . После чего определяется суммарный действующий изгибающий момент: . После чего определяется суммарный действующий изгибающий момент: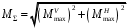 и определяются изгибающие напряжения, действующие в материале вала: 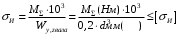 Вал II признаётся пригодным для использования в данном механизме, если фактические напряжения в нём не превышают предельных для материала, из которого он изготавливается. Проверочные расчёты зубчатых колёс на примере цилиндрической зубчатой передачи. Проверочные расчёты на прочность любой зубчатой передачи производятся по двум параметрам: контактным напряжениям 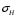 и напряжениям изгиба и напряжениям изгиба 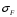 , измеряемым в МПа. , измеряемым в МПа.Зубья зубчатых колёс в процессе работы подвергаются двум видам нагрузок – смятию и изгибу, причём их взаимодействие друг с другом идёт по некоторой площади, называемой «пятном контакта» или «линией контакта». 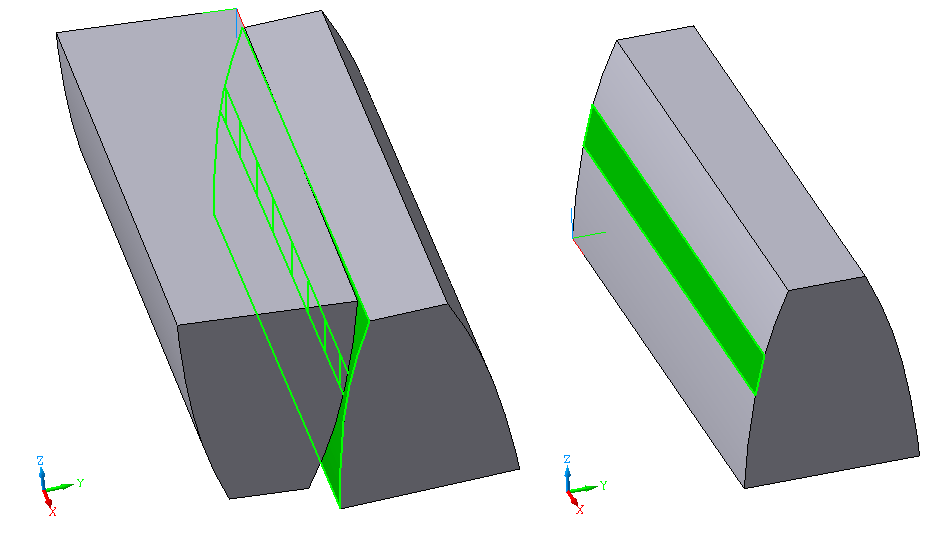 Поскольку металл зуба всегда обладает определённой упругостью, то под действием нагрузки от зуба соседнего колеса он немного деформируется в зоне пятна контакта, а после снятия нагрузки, принимает первоначальную форму. Такая совокупность однократного приложения и снятия нагрузки к зубу носит название «цикла нагружения», причём зуб по всей поверхности контакта испытывает знакопеременные нагрузки последовательного растяжения-сжатия, считающиеся в «Сопротивлении материалов» знакопеременными и наиболее опасными для деталей машин и конструкций, потому, что в этом случае после некоторого числа циклов нагружения в материалах начинают развиваться усталостные микротрещины, способные приводить к аварийным ситуациям по мере их углубления в металл. С точки зрения упреждения нежелательных последствий прочностной расчёт зуба колеса следует рассматривать по двум параметрам: контактным напряжениям усталости, возникающим вследствие местных деформаций в пятне контакта и влекущим появление микротрещин; напряжениям изгиба, возникающим по высоте зуба и влекущим его излом в определённый момент времени.  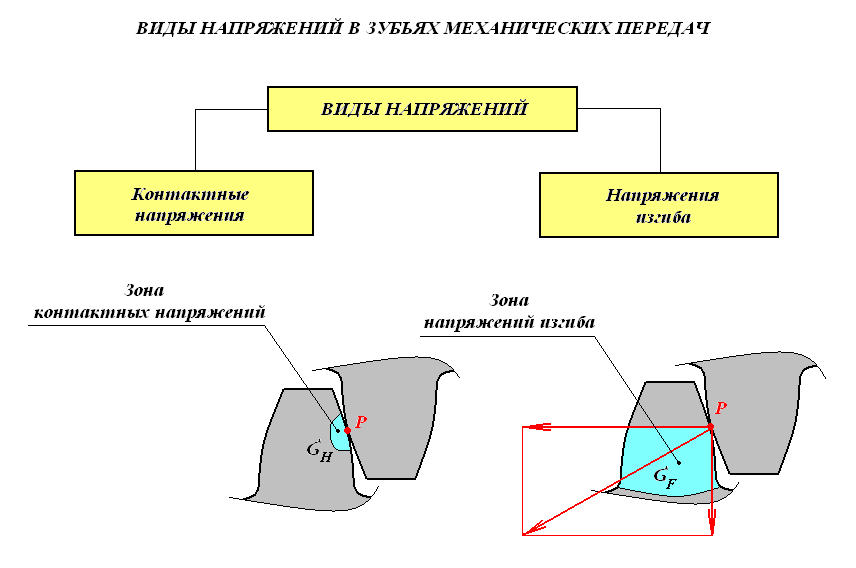 Простейшие расчётные зависимости для подобных случаев известны из курса «Сопротивления материалов» и для изображённых расчётных схем пятна контакта и зуба целиком выглядят следующим образом. Окружная сила взаимодействия зубьев колёс друг с другом: 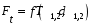 , ,где Т1,2 – крутящий момент на зубчатом колесе 1 или 2 (Нм); d1,2 – диаметр зубчатого колеса 1 или 2 соответственно (м), практически полностью распределяется по поверхности контакта, создавая на ней распределённую нагрузку: 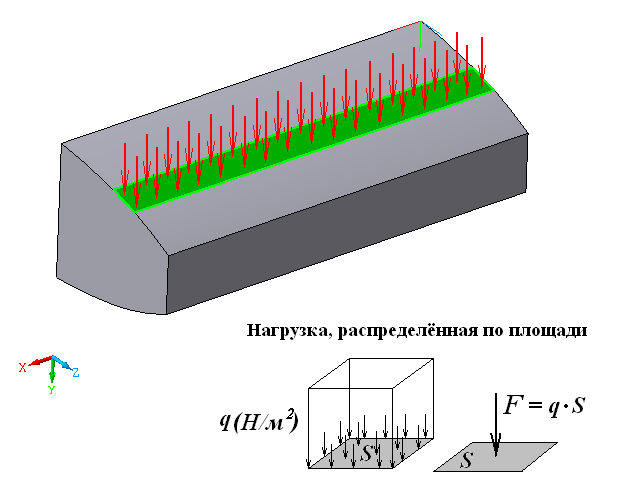 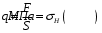 То есть в лабораторных условиях, имея возможность измерить фактическое пятно контакта и зная значения сил, моментов и диаметры колёс, получить примерное значение контактных напряжений не составит большого труда. Аналогично, расчётная схема зуба на изгиб и простейший расчёт напряжений изгиба у его основания выглядит следующим образом: 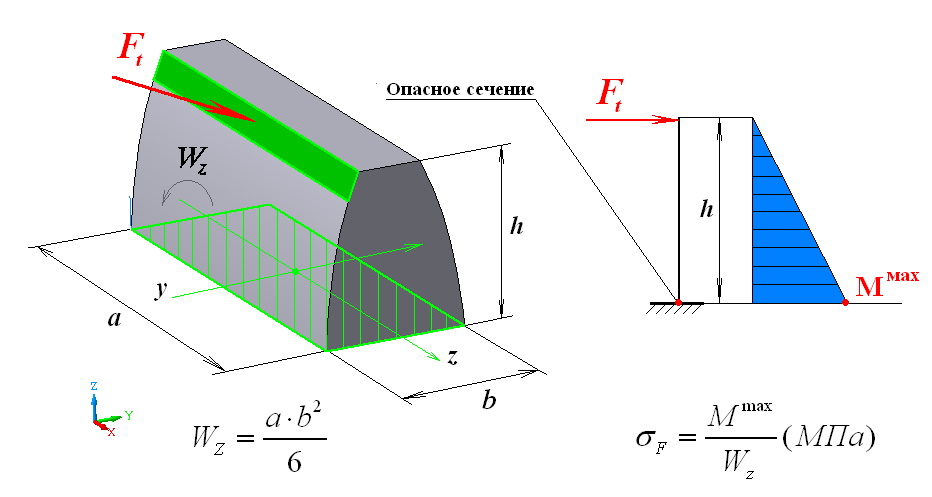 В общем случае зуб колеса может быть рассмотрен, как «жёсткая заделка», нагруженная в своей вершине силой 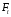 . Опасным сечением в этом случае будет площадь основания зуба, изгибающий момент M в которой будет максимальным и которая будет оказывать сопротивление изгибу, численно равное значению: . Опасным сечением в этом случае будет площадь основания зуба, изгибающий момент M в которой будет максимальным и которая будет оказывать сопротивление изгибу, численно равное значению: 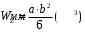 , ,где а и b – размеры основания зуба (мм). Соответственно, изгибающие напряжения в плоскости основания: 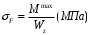 Необходимо отметить, что изложенная методика расчёта напряжений является иллюстрирующей и необходимой для общего понимания механизмов действия нагрузок на материал и расчёта напряжений, в нём возникающих. С точки зрения практического проектировочного расчёта зубьев колёс она не даёт эффективного результата по следующим причинам: в идеальных расчётах по «сопротивлению материалов» делаются ряд допущений, предполагающих например однородность тел, одинаковость их реакций на нагрузки внутри материала во всех направлениях и т.п. В реальных деталях это часто не так. в идеальном случае нагрузка на зубья равномерно распределяется по всей их длине. В реальном случае это не так. существует ещё ряд мелких деталей, которые сложно спрогнозировать при предварительном расчёте передачи, но при этом они влияют на его конечный результат. Поэтому в результирующие зависимости для определения контактных напряжений и напряжений изгиба, которые используются сегодня в прочностных расчётах зубчатой передачи, включён целый ряд поправочных коэффициентов, с учётом многолетнего опыта проектирования передач, минимизирующих влияние перечисленных выше факторов на точность расчёта. Эти зависимости приводятся в большинстве справочников по проектированию деталей машин, например Н.Г. Куклина, А.Е. Шейнблита и др. и выглядят так: 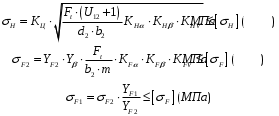 Конкретные значения коэффициентов в указанных формулах зависят от условий эксплуатации передач и принимаются по справочным таблицам. 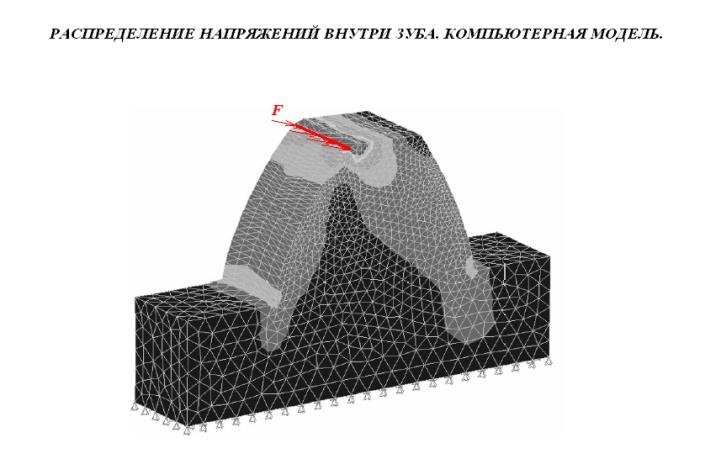 ЛЕКЦИЯ 13,14 Валы, оси, подшипники и уплотнительные устройства Валы и подшипники Валы и оси Валы и оси являются элементами, предназначенными для крепления частей механизма, непосредственно участвующих в передаче вращательного движения (шкивы, звёздочки, зубчатые и червячные колёса и т.п.). 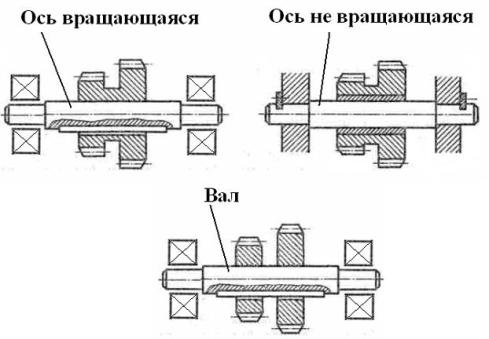 Отличие валов и осей Вал – деталь машины или механизма предназначенная для передачи вращающего или крутящего момента вдоль своей осевой линии. Большинство валов – это вращающиеся (подвижные) детали механизмов, на них обычно закрепляются детали, непосредственно участвующие в передаче вращающего момента (зубчатые колёса, шкивы, звёздочки цепных передач и т.п.). Ось – деталь машины или механизма, предназначенная для поддержания вращающихся частей и не участвующая в передаче вращающего или крутящего момента.Ось может быть подвижной или неподвижной. Классификация валов и осей: 1. По форме продольной геометрической оси: 1.1.прямые(продольная геометрическая ось – прямая линия), например, валы редукторов, валы коробок передач гусеничных и колёсных машин; 1.2. коленчатые(продольная геометрическая ось разделена на несколько отрезков, параллельных между собой смещённых друг относительно друга в радиальном направлении), например, коленвал двигателя внутреннего сгорания; 1.3. гибкие(продольная геометрическая ось является линией переменной кривизны, которая может меняться в процессе работы механизма или при монтажно-демонтажных мероприятиях), часто используются в приводе спидометра автомобилей.    Прямой, гибкий и коленчатый валы 2. Прямые валы по форме исполнения и наружной поверхности: 3.1. гладкие валы имеют одинаковый диаметр по всей длине; 3.2. ступенчатые валы отличаются наличием участков отличающихся друг от друга диаметрами; 3.3. полыевалы снабжены сквозным или глухим отверстием, соосным наружной поверхности вала и простирающимся на большую часть длины вала; 3.4. шлицевые валы по внешней цилиндрической поверхности имеют продольные выступы – шлицы, равномерно расположенные по окружности и предназначенные для передачи моментной нагрузки от или к деталям, непосредственно участвующим в передаче вращающего момента; 3.5. валы, совмещённые с элементами, непосредственно участвующими в передаче вращающего момента (вал-шестерня, вал-червяк).     Гладкие,ступенчатые, шлицевой, полый валы и вал-шестерня Конструктивные элементы валов представлены на рисунках Опорные части валов и осей, через которые действующие на них нагрузки передаются корпусным деталям, называются цапфами. Цапфу, расположенную в средней части вала, обычно называют шейкой. Концевую цапфу вала, передающую корпусным деталям только радиальную нагрузку или радиальную и осевую одновременно, называют шипом, а концевую цапфу, передающую только осевую нагрузку, называют пятой. С цапфами вала взаимодействуют элементы корпусных деталей, обеспечивающие возможность вращения вала, удерживающие его в необходимом для нормальной работы положении и воспринимающие нагрузку со стороны вала. Соответственно элементы, воспринимающие радиальную нагрузку (а часто вместе с радиальной и осевую) называют подшипниками, а элементы, предназначенные для восприятия только осевой нагрузки – подпятниками.
Кольцевое утолщение вала малой протяжённости, составляющее с ним одно целое и предназначенное для ограничения осевого перемещения самого вала или насаженных на него деталей, называют буртиком. Переходная поверхность от меньшего диаметра вала к большему, служащая для опирания насаженных на вал деталей, называется заплечиком. 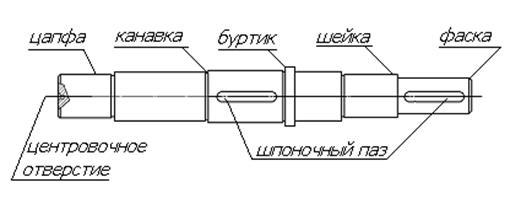 Основные элементы вала. Переходная поверхность от цилиндрической части вала к заплечику, выполненная без удаления материала с цилиндрической и торцевой поверхности называется галтелью. Галтель предназначается для снижения концентрации напряжений в переходной зоне, что в свою очередь ведёт к увеличению усталостной прочности вала. Чаще всего галтель выполняют в форме радиусной поверхности однако в отдельных случаях галтель может быть выполнена в форме поверхности переменной двойной кривизны.Последняя форма галтели обеспечивает максимальное уменьшение концентрации напряжений, однако требует выполнения специальной фаски в отверстии насаживаемой детали.
Углубление малой протяжённости на цилиндрической поверхности вала, выполненное по радиусу к оси вала, называют канавкой. Канавка, также как и галтель, очень часто используется для оформления перехода от цилиндрической поверхности вала к торцевой поверхности его заплечика. Наличие канавки в этом случае обеспечивает благоприятные условия для формирования цилиндрических посадочных поверхностей, так как канавка является пространством для выхода инструмента, формирующего цилиндрическую поверхность при механической обработке (резец, шлифовальный круг). Однако канавка не исключает возможности образования ступеньки на торцевой поверхности заплечика. Углубление малой протяжённости на торцевой поверхности заплечика вала, выполненное вдоль оси вала, называют поднутрением. Поднутрение обеспечивает благоприятные условия для формирования торцевой опорной поверхности заплечика, так как является пространством для выхода инструмента, формирующего эту поверхность при механической обработке (резец, шлифовальный круг), но не исключает возможности образования ступеньки на цилиндрической поверхности вала при её окончательной обработке. Обе указанные проблемы решает введение в конструкцию вала наклонной канавки, которая совмещает достоинства, как цилиндрической канавки, так и поднутрения.
Цапфы валов могут иметь форму различных тел вращения: цилиндрическую, коническую или сферическую. Шейки и шипы чаще всего выполняют в форме цилиндра. Цапфы такой формы достаточно технологичны при изготовлении и ремонте и широко применяются как с подшипниками скольжения, так и с подшипниками качения. В форме конуса выполняют концевые цапфы валов, работающие, как правило, с подшипниками скольжения, с целью обеспечения возможности регулировки зазора и фиксации осевого положения вала. |