Конспект лекций (wecompress.com). Лекция основные понятия и определения

• Название: Лекция основные понятия и определения
• Дата: 29.10.2022
• Размер: 5.8 Mb.
• Имя файла: Конспект лекций (wecompress.com).docx
• Тип: Лекция; #760885
• страница: 4 из 10

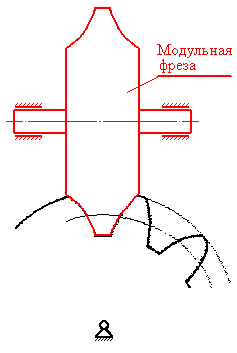
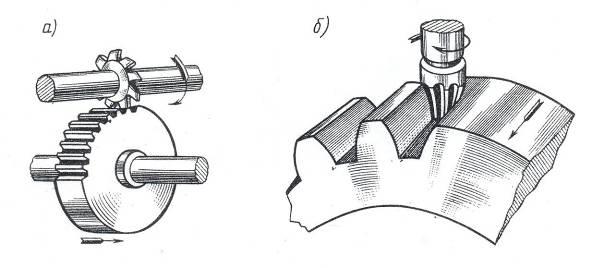
Вообще говоря, все методы изготовления зубчатых колес можно разбить на две категории: метод копирования; метод обкатки.

Метод копирования. Исторически это первая категория методов, которые стали применять для изготовления “правильных” зубчатых колес, т.е. таких, зацепление которых отвечает основной теореме зацепления. Суть метода сводится к тому, что изготавливают инструмент, рабочая поверхность которого имеет форму зуба нарезаемого колеса. На рис. 32 дан пример, когда колесо изготавливается с помощью модульной фрезы. К методу копирования относится и штамповка колес.

Метод копирования

К преимуществам этого метода относится возможность изготовления любого типа колес, с любым профилем зубьев. Что и обусловило применение этого метода главным образом для изготовления колес c неэвольвентным профилем зубьев.

Основным недостатком метода является его относительно высокая стоимость, т.к. для каждого типоразмера колеса требуется свой инструмент. Инструмент этот имеет весьма сложную форму рабочей поверхности. Рабочая поверхность должна иметь очень высокую твердость, следовательно, для обработки такой поверхности требуется инструмент еще более высокой твердости, и оснастка получается весьма дорогостоящей. Таким образом, применение метода копирования целесообразно для колес с не эвольвентным профилем зубьев или при массовом или крупносерийном производстве.





Изготовление колес методом копирования

Метод обкатки. Этим методом можно изготовить только колеса с эвольвентным профилем зубьев. Инструментом в данном случае может являться: режущая рейка, червячная фреза или долбяк. Показана схема изготовления колеса методом обкатки режущей рейкой. Движение резанья происходит перпендикулярно плоскости рисунка.

Изготовление колеса методом обкатки

Если инструмент и заготовка расположены друг относительно друга так, что делительная прямая режущей рейки касается делительной окружности колеса, то говорят, что колесо изготавливается без смещения инструмента (коэффициент смещения x = 0). Смещение инструмента от центра заготовки называется положительным, к центру – отрицательным. Величина смещения равна xm.

К недостаткам метода можно отнести то, изготовить можно только колеса с эвольвентным профилем зубьев.

К преимуществам этого метода относится его относительная дешевизна. Т.к. во-первых, режущие кромки, например, режущей рейки прямолинейны и их обработка гораздо дешевле, чем для инструмента в методе копирования. А во-вторых, инструмент более универсален: одной и той же рейкой можно изготавливать различные колеса с одним модулем.
Простейшие цилиндрические зубчатые передачи (с внешним и внутренним зацеплением) могут образовывать более сложные системы, которые называют ступенчатыми (рядными) передачами.
Передаточное число простейшей ступени определяется какi = z₂ / z₁. При последовательном соединении ступеней общее передаточное число определяется как произведение передаточных чисел ступеней i_общ = i₁ · i₂.
Конические зубчатые передачи

Конические ЗП – зубчатые передачи в которых зубчатый венец на звеньях сформирован по конической поверхности, при этом оси колес пересекаются.

К онические колёса сложнее цилиндрических по своей геометрии и в изготовлении, принципы силового взаимодействия, условия работы аналогичны цилиндрическим.

Конические зубчатые передачи

В эквивалентных цилиндрических колёсах диаметр начальной окружности и модуль соответствуют среднему сечению конического зуба, вместо межосевого расстояния берётся среднее конусное расстояние.



Виды конических зубчатых колёс.


Конический зубчатый редуктор

Простейшие конические зубчатые передачи могут образовывать более сложные системы, которые называют ступенчатыми (рядными) передачами.

Передаточное число простейшей ступени определяется какi = z₂ / z₁. При последовательном соединении ступеней общее передаточное число определяется как произведение передаточных чисел ступеней i_общ = i₁ · i₂.

Червячная передача

Червячная передача – это передача, два подвижных звена которой, червяк и червячное колесо, образуют совместно высшую зубчато-винтовую кинематическую пару.

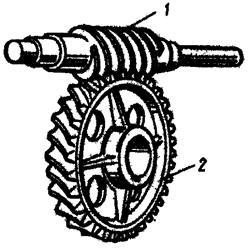Червячная передача: 1 – червяк; 2 – червячное колесо.

Достоинства червячных передач: 1) компактность и небольшая масса 2) большие передаточные числа 3) высокая плавность и кинематическая точность; 4) низкий уровень шума и вибраций; 5) самоторможение при обратной передаче движения.

Недостатки червячных передач: 1) Низкий КПД и высокое тепловыделение; 2) повышенный износ и уменьшенный срок службы; 3) склонность к заеданию.

Классификация червячных передач:

1. по направлению линии витка червяка –

1.1. правые (при наблюдении с торца червяка и его вращении по часовой стрелке червяк вкручивается в пространство - уходит от наблюдателя);

1.2.  левые(при наблюдении с торца червяка и его вращении по часовой стрелке червяк выкручивается из пространства - идёт на наблюдателя);

2.     по форме делительной поверхности червяка –

2.1. с цилиндрическим червяком (образующая делительной поверхности – прямая линия);

2.2.   с глобоидным червяком (образующая делительной поверхности – дуга окружности, совпадающая с окружностью делительной поверхности червячного колеса);

3.     по форме боковой (рабочей) поверхности витка червяка –

3.1.    с архимедовым червяком, профиль зуба в сечении параллельном оси червяка – трапеция (обозначается ZA);

3.2.    с конволютным червяком, профиль зуба в сечении перпендикулярном виткам червяка – трапеция (обозначается ZN);

3.3.    с эвольвентным червяком, профиль зуба в сечении перпендикулярном виткам червяка – эвольвентный (обозначается ZI).

Форма боковой поверхности червяка мало влияет на работоспособность червячной передачи и, в основном, связана с выбранной технологией изготовления червяка.



Червячный зубчатый редуктор

Червяк может иметь различное число заходов (обычно 1 – 4), оно определяется количеством витков (ниток) нарезки зуба, идущих друг от друга на расстоянии шага и имеющих свое начало на торцах нарезанной части червяка.

Передаточное число червячной передачи определяется какi = z₂ / k, где z₂ – число зубьев червячного колеса, k– число заходов червяка.

Планетарные передачи

Планетарной называется передача, имеющая в своём составе зубчатые колёса с перемещающимися геометрическими осями, которые называют сателлитами.





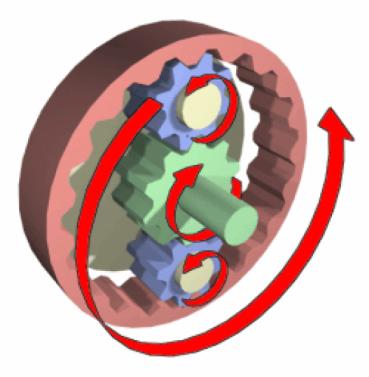
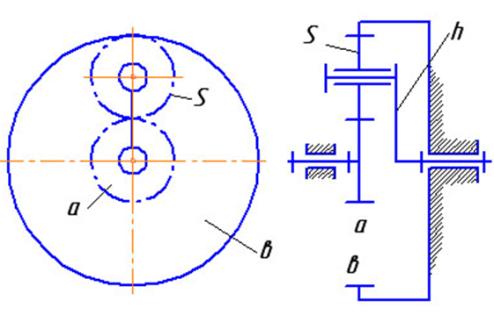
Планетарная передача схемы А

Рассмотрим простейшую планетарную передачу схемы А.

Колёса, геометрические оси которых совпадают с общей осью передачи (с осью входного и выходного валов), называют центральными. Центральное колесо с зубьями на внешней стороне обода, то есть направленными от оси вращения колеса, называют солнечной шестерней, а второе центральное колесо, взаимодействующее с сателлитами внутренними зубьями, то есть направленными к оси колеса, называют эпициклическим или просто эпициклом. Звено, несущее на себе подвижные оси сателлитов, называют водилом. На кинематических схемах зубчатые колёса обычно обозначают арабскими цифрами, а водило – буквой H или h.

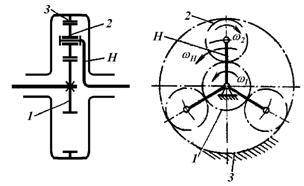Планетарная передача А (кинема­тическая схема): 1 – солнечное колесо; 2– сателлит; 3 – эпицикл; H – водило.

Планетарный ЗМ, у которого ни одно из звеньев не соединено со стойкой, обладает двумя степенями свободы, т.е. является дифференциальным механизмом. Если же в планетарном дифференциальном механизме одно из звеньев соединить со стойкой, то такой механизм превращается в передачу. Связывание со стойкой (или между собой) разных звеньев дифференциального планетарного ряда ведёт к изменению передаточного числа планетарной передачи.

Планетарные механизмы обеспечивает следующие преимущества:

1.     уменьшение габаритов; 2.     высокую надежность работы; 3.     высокий КПД; 4. большие передаточные числа; 5.     отсутствие поперечной нагрузки на основных валах.

Недостатки планетарных передач: 1.увеличение сложности; 2.повышение стоимости.

Особенности проектирования и расчёта планетарных передач связаны с наличием нескольких сателлитов.



Сателлиты планетарной передачи

Предельно возможное число сателлитов в одном планетарном ряду ограничивается условием соседства, которое гласит: число сателлитов в планетарном ряду должно быть таким, чтобы соседние сателлиты не касались друг друга. Но в практике машиностроения число сателлитов редко принимают более шести.

Второенеобходимоеусловие существования планетарного ряда называется условием соосности. Суть его вытекает из необходимости соблю­дения соосности центральных колёс, солнечного и эпицикла, и водила. Для простого планетарного ряда это условие выливается в равенство межосевых расстояний зацепления солнечного колеса с сателлитом и зацепления са­теллита с эпициклом.



Планетарный зубчатый редуктор

Передаточное число планетарной передачи схемы А определяется какi = 1 + (z₃ / z₁), где z₃ – число зубьев эпицикла (неподвижного центрального колеса с внутренним зацеплением), z₁ – число зубьев центрального (солнечного) колеса. Обратите внимание, что на передаточное число не влияют число зубьев и количество сателлитов.

Волновые передачи

Волновыми называют зубчатые механические передачи, включающие контактирующие между собой гибкое 2 и жёсткое ЗК 1, обеспечивающие работу при деформировании гибкого зубчатого колеса за счет движения генератора волн 3.



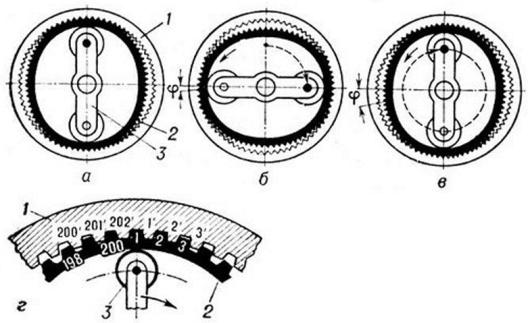
Работа волновой передачи

Достоинства волновых передач:

1. большое передаточное число (до 320); 2. большое число зубьев, одновременно находящихся в зацеплении (от 40 до 80%); 3.высокая кинематическая точность; 4. высокий КПД; 5. отсутствие поперечной нагрузки на основных валах. 6. низкий уровень шума;

Недостатки волновых передач:

1. высокая стоимость; 2. сложность изгото­вления гибкого колеса; 3. относительно низкий срок службы.

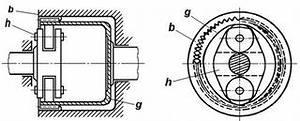Волновая зубчатая передача

Волновой механизм, аналогично планетарному является дифференциальным. В состав ВМ входят генератор волн h, жесткое колесо b, и гибкое колесо g

Различных вариантов конструкций ВМ множество, рассмотрим простейшую – с симметричной двухволновой схемой деформации гибкого колеса, позволяющая исключить возможность возникновения поперечных нагрузок на валах передачи.



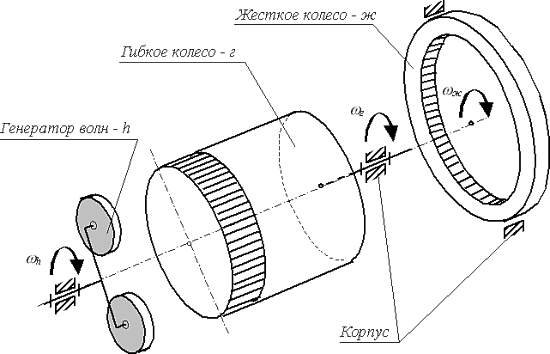
Устройство волновой передачи с генератором волн

В большинстве известных конструкций гибким является колесо с внешним зубчатым венцом, а жёсткое колесо снабжено внутренними зубьями. Обычно бывает наиболее удобным конструктивно входной вал редуктора соединить с генератором волн, а выходной с гибким колесом, в этом варианте конструкция редуктора получается наиболее компактной и технологичной.



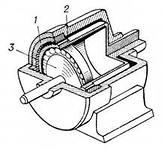
Волновой редуктор с гибким подшипником

ЛЕКЦИЯ 11,12

Основные расчеты параметров механических передач



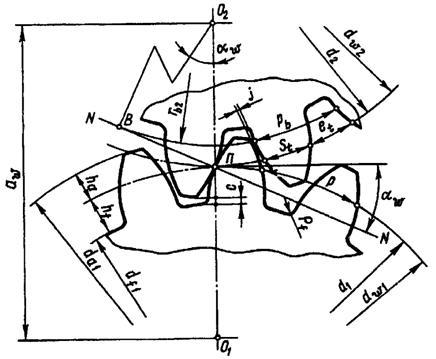
Геометрические параметры эвольвентного зубчатого зацепления

Основные параметры эвольвентных зубчатых передач стандартизированы при обозначении параметром шестерни приписывается индекс «1», параметрам колеса «2»

1.       О₁,О₂ – центры вращения зубчатых колес;

2.       Межосевое расстояние (а_w) - расстояние между осями зубчатых колес О₁ и О₂ (a_w=(d_w1+d_w2)/2);

3.       Линия зацепления (NN) - геометрическое место точек контакта между сопряженными профилями зубьев;

4.       Угол зацепления (α_w) - угол между линией зацепления и перпен­дикуляром к О₁О₂(стандартный угол зацепления α_w = 20°);

5.       Основная окружность (d_b1 и d_b2) - окружность, образующая эвольвенту, касаются в полюсе зацепления (d_b=d_w·Cosα_w).

6.  делительные окружности (d_W1, d_W2,равные начальнымd₁, d₂) – окружности зубчатых колес, делящие зуб на две примерно равные части – головку и ножку (d_w=d=m·z);

7.       Окружность выступов (d_a1, d_a2) – окружность, очерченная по вершинам зубьев (d_a=d_w+2·h_a=m·(z+2·h^*_a), h^*_a – коэффициент высоты головки зуба, обычно h^*_a = 1).

8.       Окружность впадин (d_f1, d_f2)- окружность, очерченная по дну впадин между зубьями (d_a=d_w-2·h_f=m·(z-2·(h^*_a+c^*)), c^* – коэффициент радиального зазора, обычно с^* = 0,25).

9. Торцевой шаг зубьев (р_t) – расстояние между одноименными точками боковой поверхности зубьев, измеренное по делительной окружности (p_t=π·m);

10.  Высота головки зуба (h_а) – расстояние между делительной окружностью и окружностью выступов, измеренное по радиусу (h_а= h^*_a·т).

11.  Высота ножки зуба (h_f) – расстояние между делительной окружностью и окружностью впадин, измеренное по радиусу (h_f = т·(h^*_a+ c^*)).

12.  Высота зуба (h) – складывается из высот его ножки и головки (h = h_a + h_f, h = т·( 2·h^*_a+ c^*)).

13.  Ширина зубчатого венца (b) – расстояние между торцовыми поверхностями зубчатого венца колеса.

14.  Боковой зазор в зацеплении (j) – расстояние между неконтактирующими поверхностями зубьев (j = 0,0125·m).

15.  Радиальный зазор (с) – разница между высотой ножки и головки зуба (с = c^*·т).

16. Рабочий участок линии зацепления (g)- часть линии зацепления, отсекаемая окружностями выступов сопрягаемых колес;

17.  Коэффициент торцового перекрытия (β = g /р_t) - отношение длины активной линии зацепления к основному шагу колеса, показывает сколько зубьев в среднем находятся в зацеплении.



Эвольвентный зубчатый профил