Дискретная математика (1). Лекция Составные высказывания
 Скачать 2.15 Mb.
|
Отношения.Пусть заданы два множества А и В. Найдем А Х В. Подмножество k  А Х В называется отношением из множества А во множество В.Отношения задаются знаками =, <, >,  и т.д.Пример. А={2,3,4}, B={1,4,3} A X B={(2,1),(2,4),(2,3),(3,1),(3,4),(3,3),(4,1),(4,4),(4,3)} Выделим отношения больше 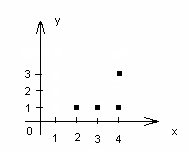>  ={(2,1),(3,1),(4,1),(4,3)}и меньше <  ={(2,4),(2,3),(3,4)} Рис.1. Отношение . Отношения на множестве.Если в декартовом произведении в качестве множества В выбрать множество А ( то есть А Х А= А  ), то отношение k из А называется отношением на множестве.Для отношений на множестве вводятся понятия: Обратное отношение-это множество пар (а,b) таких, что (b,a)  А . Дополнение-это множество пар (а,b)  k. Тождественное отношение-множество пар (а, а) таких, что, а А, I= {(a, a), a A}Универсальное отношение U={(a,b),a A, b А}Виды отношений:Инъекция. Е 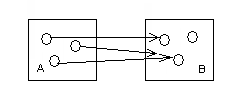 сли каждый элемент множества А соответствует элементу из множества В, то отношение f называется инъективным.Рис.2. Инъекция. Сюръекция. Если для каждого элемента y множества В существует элемент х А, соответствующий элементу y, то такое отношение f называется сюръекцией. Рис.3.Сюръекция. Биекция. Если для каждого элемента y B существует ровно один элемент х А, которому соответствует y , то такое отношение называется биективным.Биективное отношение инъективно и сюръективно. Биективное отношение имеет обратное отношение. 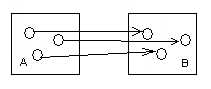 Рис.4. Биекция. Лекция 12. Отношение эквивалентности. Из содержания предыдущей лекции и рассмотренных в ней примеров видно, что понятие “отношение” следует понимать весьма широко. В данной лекции мы попытаемся ввести определённую классификацию отношений и рассмотреть наиболее значительные с точки зрения математики виды отношений – а именно отношения эквивалентности и порядка. Отношения эквивалентности. Определение.Отношение называется отношением эквивалентности (или просто эквивалентностью), если оно рефлексивно, симметрично и транзитивно. Пример. а) Отношение равенства (часто обозначается  ) на любом множестве является отношением эквивалентности. Равенство – это минимальное отношение эквивалентности в том смысле, что при удалении любой пары из этого отношения (то есть любой единицы на главной диагонали матрицы ) оно перестаёт быть рефлексивным и, следовательно, уже не является эквивалентностью.б) Утверждения вида  или  , состоящие из формул, соединённых знаком равенства, задают бинарное отношение на множестве формул, описывающих суперпозиции элементарных функций. Это отношение обычно называется отношением равносильности и определяется следующим образом: две формулы равносильны, если они задают одну и ту же функцию. Равносильность в данном случае, хотя и обозначена знаком “=”, означает не то же самое, что отношение равенства, так как оно может выполняться для различных формул. Впрочем, можно считать, что знак равенства в таких отношениях относится не к самим формулам, а к функциям, которые ими описываются. Для формул же отношение равенства – это совпадение формул по написанию. Оно называется графическим равенством. Кстати, чтобы в подобных ситуациях избежать разночтений, часто для обозначения отношения равносильности используют знак “ ”.в) Рассмотрим множество треугольников на координатной плоскости, считая, что треугольник задан, если даны координаты его вершин. Два треугольника будем считать равными (конгруэнтными), если при наложении они совпадают, то есть, переведены друг в друга с помощью некоторого перемещения. Равенство является отношением эквивалентности на множестве треугольников. г) Отношение “иметь один и тот же остаток отделения на натуральное число  ” на множестве натуральных чисел является отношением эквивалентности.е) Отношение “быть делителем” не является на множестве  отношением эквивалентности. Оно обладает свойствами рефлексивности и транзитивности, но является антисимметричным (см. ниже).Пусть на множестве  задано отношение эквивалентности  . Осуществим следующее построение. Выберем элемент  и образуем класс  (подмножество  ), состоящий из элемента  и всех элементов, эквивалентных ему в рамках данного отношения. Затем выберем элемент  и образуем класс  , состоящий из  и эквивалентных ему элементов. Продолжая эти действия, получим систему классов  (возможно, бесконечную) такую, что любой элемент из множества входит хотя бы в один класс, то есть  . Эта система обладает следующими свойствами: она образует разбиение множества , то есть классы попарно не пересекаются;любые два элемента из одного класса эквивалентны; любые два элемента из разных классов не эквивалентны. Все эти свойства прямо следуют из определения отношения эквивалентности. Действительно, если бы, например, классы  и  пресекались, то они имели бы хотя бы один общий элемент. Этот элемент был бы, очевидно, эквивалентен и . Тогда, в силу транзитивности отношения выполнялось бы  . Однако, по способу построения классов, это не возможно. Аналогично можно доказать другие два свойства.Построенное разбиение, то есть система классов – подмножеств множества , называется системой классов эквивалентности по отношению . Мощность этой системы называется индексом разбиения. С другой стороны, любое разбиение множества на классы само определяет некоторое отношение эквивалентности, а именно отношение “входить в один класс данного разбиения”.Пример . а) Все классы эквивалентности по отношению равенства состоят из одного элемента.б) Формулы, описывающие одну и ту же элементарную функцию, находятся в одном классе эквивалентности по отношению равносильности. В данном случае счётными являются само множество формул, множество классов эквивалентности (то есть индекс разбиения) и каждый класс эквивалентности. в) Разбиение множества треугольников по отношению равенства имеет континуальный индекс, причём каждый класс имеет также мощность континуум. г) Разбиение множества натуральных чисел по отношению “иметь общий остаток при делении на 7” имеет конечный индекс 7 и состоит из семи счётных классов. Отношения порядка. Определение 1. Отношение называется отношением нестрогого порядка, если оно является рефлексивным, антисимметричным и транзитивным.Определение 2. Отношение называется отношением строгого порядка, если оно является антирефлексивным, антисимметричным и транзитивным.Оба типа отношений вместе называются отношениями порядка. Элементы  сравнимы по отношению порядка , если выполняется одно из двух отношений  или  . Множество , на котором задано отношение порядка, называется полностью упорядоченным, если любые два его элемента сравнимы. В противном случае, множество называется частично упорядоченным. Пример. а) Отношения “  ” и “ ” являются отношениями нестрогого порядка, отношения “<” и “>” – отношениями строгого порядка (на всех основных числовых множествах). Оба отношения полностью упорядочивают множества и .б) Определим отношения “ ” и “<” на множестве  следующим образом: 1)  , если  ;2)  , если и при этом ходя бы для одной  координаты выполняется  . Тогда, например,  , но  и  несравнимы. Таким образом, эти отношения частично упорядочивают .,в) На системе подмножеств множества отношение включения “ ” задаёт нестрогий частичный порядок, а отношение строгого включения “ ” задаёт строгий частичный порядок. Например,  , а  и  не сравнимы.г) Отношение подчинённости в трудовом коллективе создаёт строгий частичный порядок. В нём, например, несравнимыми являются сотрудники различных структурных подразделений (отделов и т. п.). д) В алфавите русского языка порядок букв зафиксирован, то есть всегда один и тот же. Тогда этот список определяет полное упорядочение букв, которое называется отношением предшествования. Обозначается  ( предшествует  ). На основании отношения предшествования букв построено отношение предшествования слов, определяемое примерно, таким образом, как производится сравнение двух десятичных дробей. Это отношение задаёт полное упорядочение слов в русском алфавите, которое называется лексикографическим упорядочением.Пример. а) Наиболее известным примером лексикографического упорядочения слов является упорядочение слов в словарях. Например,  (так как  ), поэтому слово лес расположено в словаре раньше слова лето.б) Если рассматривать числа в позиционных системах счисления (например, в десятичной системе) как слова в алфавите цифр, то их лексикографическое упорядочение совпадает с обычным, если все сравниваемые числа имеют одинаковое количество разрядов. В общем же случае эти два вида могут не совпадать. Например,  и  , но  , а  . Для того, чтобы они совпадали, нужно уравнять число разрядов у всех сравниваемых чисел, приписывая слева нули. В данном примере при этом получим  . Такое выравнивание происходит автоматически при записи целых чисел в ЭВМ.в) Лексикографическое упорядочивание цифровых представлений дат вида 19.07.2004 (девятнадцатое июля две тысячи четвёртого года) не совпадает с естественным упорядочением дат от более ранних к более поздним. Например, дата 19.07.2004 “лексикографически” старше восемнадцатого числа любого года. Чтобы возрастание дат совпадало с лексикографическим упорядочением, обычное представление надо “перевернуть”, то есть записать в виде 2004.07.19. так обычно делают при представлении дат в памяти ЭВМ. Лекция 13. Композиция отображений |