Дискретная математика (1). Лекция Составные высказывания

• Название: Лекция Составные высказывания
• Дата: 05.09.2022
• Размер: 2.15 Mb.
• Имя файла: Дискретная математика (1).doc
• Тип: Лекция; #662788
• страница: 11 из 16

Равенство соответствий

Утверждение.Пусть соответствие f, g Í АхВ, А, В , f=g  когда аÍ А, f(а)=g(а).

Образ и прообраз множества

Пусть нам даны множества А₁, В₁, А, В , f Í АхВ связаны А₁ Í А_, В₁Í В.

Образом множества А₁ будем называть , а полным прообразом множества В₁ .

Пример. f Í RхR

f(х)=х²
f([-1;1])=[0;1]

А₁=[-1;1]

В₁=[-2;-1]

f^-1([-2;-1])=0

f^-1([-1;0])=0 f^-1([1;2])=[1;2][-2;-1]

f([1;4])=[1;16]

Произведение соответствий (композиция)

Определение.Пусть нам даны соответствия fÍ АхВ, gÍ CхD, то композицию соответствия gf будет представлять собой gf Í АхD и действовать так:
"а Î А: (gf)(а)= g(f(а))

Пример. f Í Rх[-1;1] g Í [-1;2]х[-4;8]

f(х)=sinх g(х)=4х

Нужно построить gf и fg.

gfÍ Rх[-4;8] fgÍ [-1;2]х[-1;1]

1) фиксируем элемент хR

(gf)(х)= g(f(х))= 4sinх

2) фиксируем элемент х[-1;2]

(fg)(х)=f(g(х))= 4sinх

Пример. f Í АхВ Í СхD

f_А,В _{С, D}= _{C, В}

g Í FхE Í PхL

_{P, L}g_{F, E}= _{F, L}

Утверждение.Пусть нам даны два соответствия f Í АхВ и , g Í СхD, для того, чтобы их композиция представляла не пустое соответствие gf  E_f  D_g .

Доказательство:

Необходимость:

Дано: gf

Доказать: E_f  D_g .

Доказательство:

gf  существует а А: (gf)(а)   g(f(а))  

существует d D:d g(f(а)) 

существует b f(а); b Е_f  b D_g  b E_f  D_g .

Достаточность:

Дано: E_f  D_g

Доказать: gf

Доказательство:

E_f  D_g  найдется такой элемент с E_f и с D_g.

существует а А: с f(а); существует d D: d g(с), g(с) Í g(f(а))

по определению отношения включения d g(f(а))  d (gf)(а)  gf .

Свойства ассоциативности для композиции соответствий

fÍ АхВ, gÍ CхD, hÍ EхF

h (gf)= (h g)f

gf Í АхD h (gf) Í АхF (h g)f Í АхE

Докажем свойство ассоциативности h (gf), (h g)fÍ АхF.

Зафиксируем элемент а А и подействуем на него (h (gf))(а)= h (gf)(а)= h(g(f(а))= (h g)(f(а))= ((h g) f)(а).

Композиция отображений. Ее свойства

Пусть f:АВ, g:ВC, тогда

1 gf является отображением и действием

gf: АC

2 если g и f инъективные отображения, то и композиция gf также инъективное отображение

3 если g и f сюръективные отображения, то и композиция gf - сюръективное отображение

4 если g и f биективные отображения, то и композиция gf - биективное отображение

1 Пусть gf  АхC, зафиксируем аА

Доказательство:

Подействуем на этот элемент (gf)(а)= g(f(а)).

Для доказательства того, что соответствующий f является отображением можно использовать утверждение: аА f(а)=1, f  АхВ.

Из того, что f и g являются отображением  аА gf(а)=1  gf: АC.

2 Зафиксируем элементы а₁, а₂ А.

Доказательство:

Подействуем нашим отображением на а₁ (gf)(а₁)= (gf)(а₂)  а₁=а_2. Рассмотрим равенство (gf)(а₁)= g(f(а₁))= g(f(а₂))  f(а₁)= f(а₂)  а₁=а_2.

3 Дано: g и f сюръективные

Доказать: gf сюръективное отображение

Доказательство:

Покажем, что сС имеет прообраз во множестве А. Зафиксируем сС. Из того, что g сюръективно следует, что существует bB: g(b)=с.

Так как f сюръективно следует аА: f(а)=b, g(f(a))=c, (gf)(a)=c следует
gf сюръективно.

А f В g С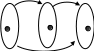



а b c

gf

4Доказательство следует из доказательств 2 и 3.
Лекция 14. Операции над подстановками.
Подстановка на множестве M – это биекция [7]:

M  N_n, n = |M|  N.

В случае конечного множества M (как выше) количество подстановок определяется как количество перестановок из n элементов:



Можно считать, n ящиков заполняются объектами x₁, …, x_n, x_i  M.

Поскольку M биективно N_n, можно определить подстановку как N_n  N_n, т.е. иметь дело только с натуральными числами:



{i₁, i₂, … , i_n} = N_n.
Обычно подстановка задается в форме стандартной таблицы, имеющей две строки. Верхняя строка всегда содержит последовательные натуральные числа, начиная с 1. В нижней строке, конечно, не должно быть повторений.

Например: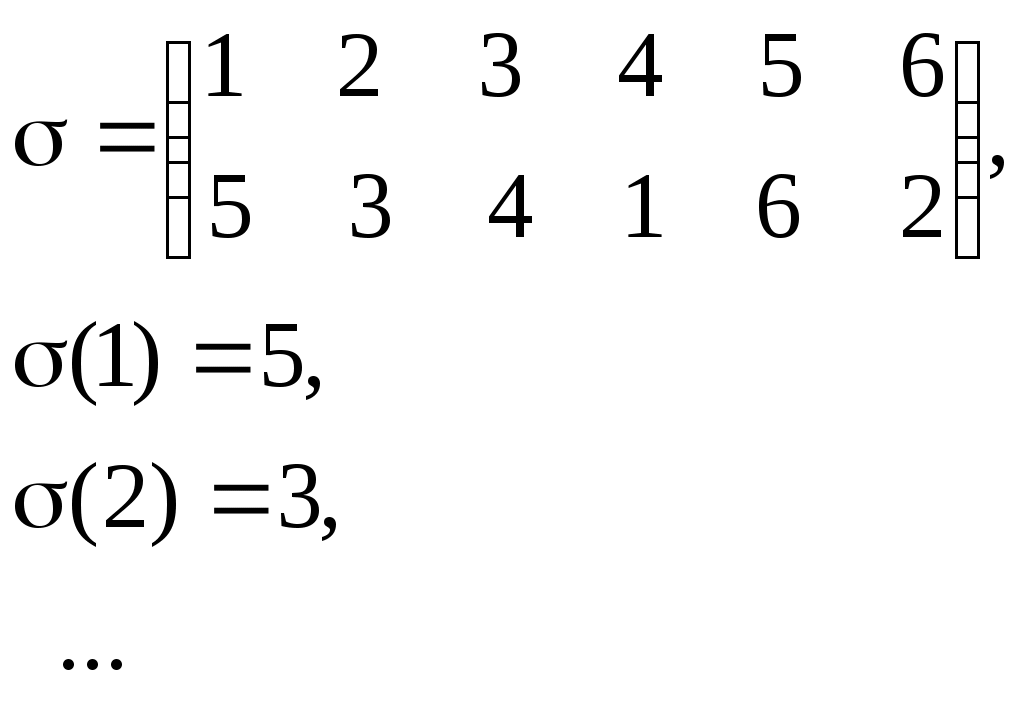



Подстановка, как и любое бинарное отношение, может быть составной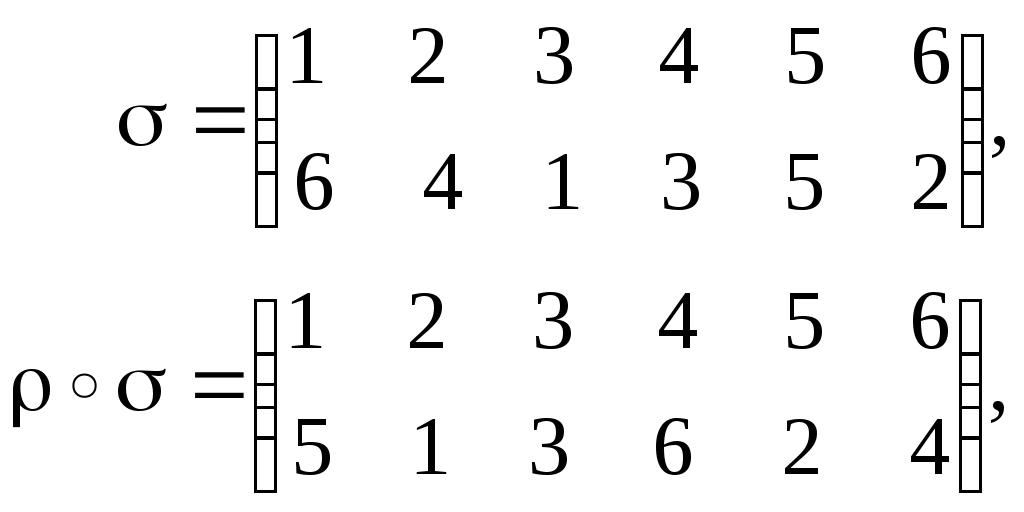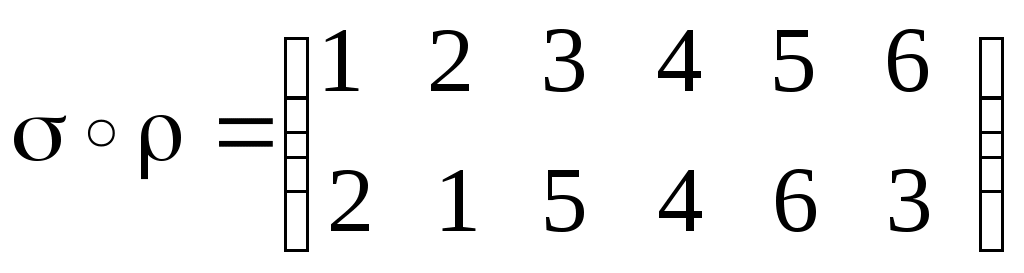



.

Видно, что в «контрпримере» , т.е. «произведение» подстановок некоммутативно.

В составе любой подстановки можно выделить циклы. Их длина может составлять 1, 2,…, n. Цикл длины 1 – это фактически вырожденный цикл, стационарный элемент.

Пример.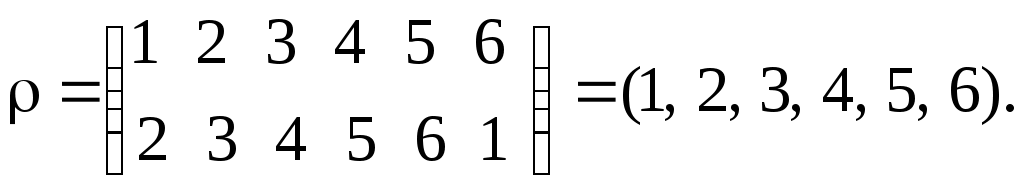



Здесь единственный цикл – типа RoL («Вращение влево»).

Пример.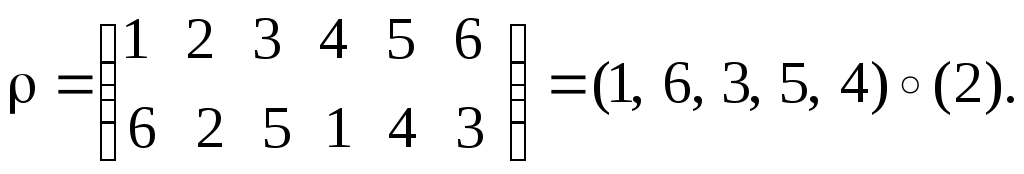



Теорема.

Любая подстановка на конечном множестве A (т.е. биективному подмножеству N_n) может быть представлена как произведение непересекающихся циклов.

Действительно, начав слева, от 1 в верхней строке, формируем первый цикл по принципу «сверху вниз, снова вверх и т.д. до замыкания на начальное значение». На основе оставшихся элементов верхней строки формируем второй цикл и т.д. Поскольку множество А (или N_n) конечное, процесс рано или поздно останавливается.

Теперь нужно показать еще непересекаемость циклов. Это следует, например, из условия неповторяемости элементов (в нижней, например, строке рис. 1).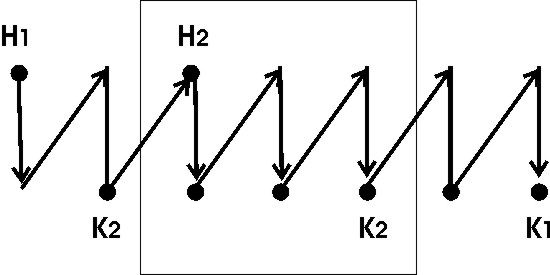

Рис. 1. К непересекаемости циклов

Доказательство от противного: пусть, наоборот, цикл 2 (H2, K2) вложен в цикл 1 (H1, K1). Тогда из-за обязательности равенств элементов на двойной стрелке (рис. 17) и K2 = H2 (замыкание) получаем в нижней строке запрещенное повторение элементов K2 .

На множестве М в отображении N  M можно определить последовательность. Например,



Функционал – это функция, определенная на множестве не простых объектов (чисел), а на множестве тоже, например, функций:



Здесь после стрелки указано множество, например, всех функций из M₂ в M₃ .

Пример.

тогда: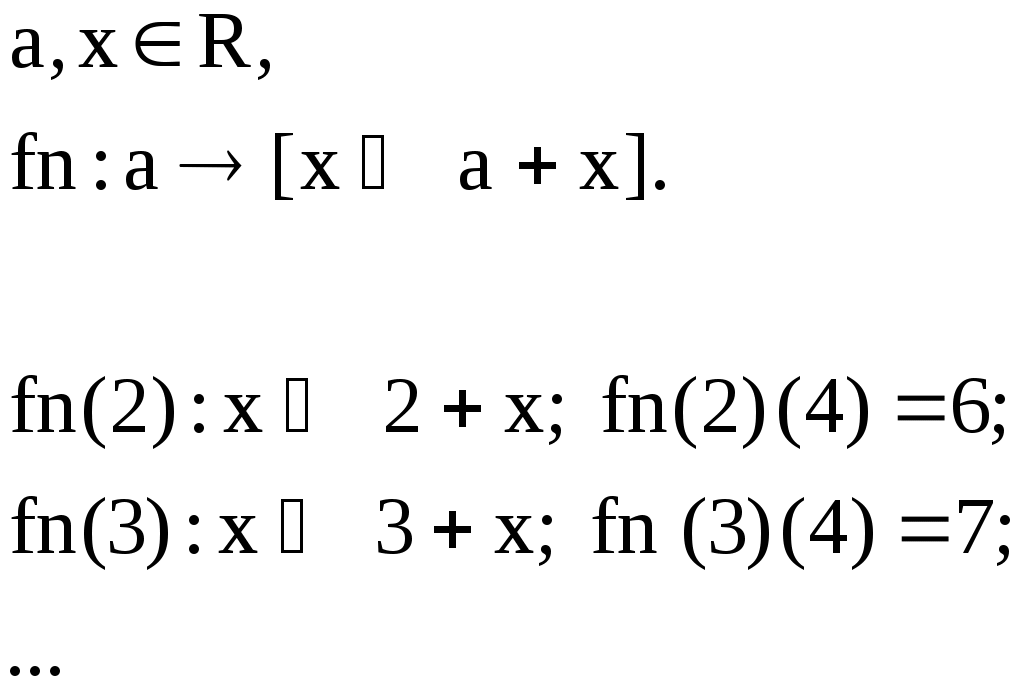
Можно считать функционал функцией с нетривиальной областью значений.

Еще один специальный случай связан с отображением, сохраняющим эквивалентность.

Пусть М – множество с -отношением эквивалентности. Тогда М разбивается этим отношением на -эквивалентные классы:

.

Итак, есть отношения эквивалентности _X и _Y определенные соответственно на множествах X и Y, и есть отображение 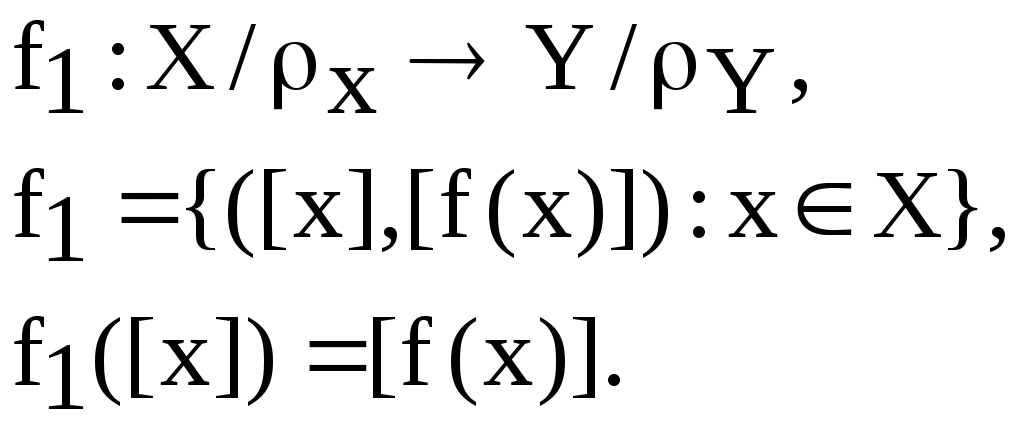. Есть еще межклассовые отношения:



Отображение f сохраняет эквивалентность, если f₁ – функция, т.е.

.

Если же f₁ – не функция, т.е. выходит за пределы класса эквивалентности (например, [х₁]), то f – не сохраняет эквивалентность.

В благоприятном же случае можно говорить: отображение f: X  Y индуцирует отображение 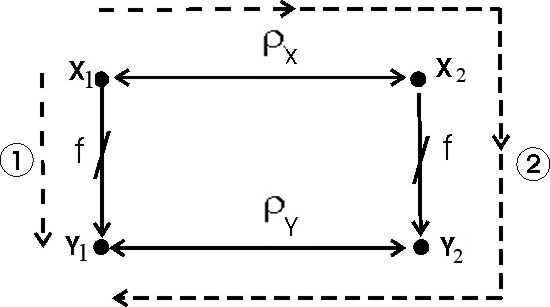(рис. 2).



Рис. 2. Графическая интерпретация отображения f,
сохраняющего эквивалентность
Видно, что существуют 2 пути от х₁ к y₁:

1: y₁ = f(x₁);

2: x₁_X x₂  y₂ = f(x₂)  y₂_Y y₁.

Пример.

X = {1, 2, 3}, Y = {1, 4, 9},

_X : X / _X = {{1}, {2, 3}},

_Y : Y / _Y ={{1},{4, 9}},

f: X  Y: x  x².

Здесь получаем:

f₁ ([1]) = [f(1)] = [1] = {1};

f₁ ([2]) = [f(2)] = [4] = {4, 9};

f₁ ([3]) = [f(3)] = [9] = {4, 9}.

Проверим f₁ на функциональность. Должно быть f₁ ([2]) = f₁ ([3]), но так и есть.

Пример.



Теперь

f₁  ([2]) = [f(2)] = [4] = {1,4};

f₁  ([3]) = [f(3)] = [9] = {9}  {1,4}.

Здесь f₁ – не функция, и замыкания двух путей нет (рис. 3).




Рис. 3. Отображение f, не сохраняющее эквивалентность

Операции

Операция над (на) множеством M это функция [7]:



Из определения операции видно, что она замкнута на множестве М, т.е. результат операции не выходит за пределы этого множества.

Еще одно свойство операции – однозначность результата, т.е.

упорядоченный набор n элементов (операндов) дает в результате операции только один элемент.

Порядок операции – это количество ее операндов: n = 1 соответствует унарной (монадической) операции, n = 2 – бинарной (диаедической) операции и т.д.

Далее рассматриваются только бинарные операции. Они могут быть заданы в одной из трех форм:

infix ( например, x + y);

prefix ( +xy );

postfix ( xy+ ).

Последние две формы дают бесскобочную запись (скобки вводятся, в инфиксной форме, для явного указания порядка выполнения операций).

Пример.

Инфиксная (обычная) форма:

a + b * c – (d – e / f).
Префиксная форма (проход и запись выражения справа налево):

+ a – * bc – d / e f.
Постфиксная форма (проход и запись слева направо), по-другому – это обратная (инверсная) польская запись (по имени польского математика Я. Лукасевича):

a b c * + d e f / – – .

Последняя форма (ОПЗ) широко используется в вычислительной технике, в частности при построении так называемых прямых трансляторов с языков программирования (используется стек с приоритетами).

Бинарная операция удобно задается таблицей (табл. 1).

Таблица 1

Операция на множестве M={a, b, c}

	a	b	c
a	a	a	b
b	b	a	c
c	a	b	b

В дальнейшем будем говорить о некоторых замечательных свойствах операций, связывая эти свойства с фиксированными номерами (1, 2, …).

1: Коммутативность.

x y = y x, x, y  M.

Например, на множестве целых чисел Z операция сложения коммутативна – в отличие от операции вычитания.

2: Ассоциативност ь.

(x y) z = x (y z), x, y, z  M.

Фактически речь идет об изменении порядка действий (задаваемого скобками).

Например, операция вычитания не ассоциативна.

3: Единица.

l x = x, l, x  M, l – левая единица.

x r = x, r, x  M, r – правая единица.

e x = x e = x, e, x  M, е – двусторонняя или просто единица.

Например, сложение на множестве вещественных чисел R имеет единицу (аддитивную):

a + 0 = 0 + a = a.

Вычитание имеет только правую единицу:

a – 0 = a, но 0 – a  a (если a  0).

Единица операции умножения (типа умножения) – мультипликативная, обозначается обычно «1» .

4: Обратный элемент.

х – левый обратный элемент по отношению к у, а у – правый по отношению х, если

х  у = е.

«Просто» обратный элемент (взаимно обратные элементы), если

х  у = у  х = е.

Существование и единственность единицы и обратного элемента позволяет решать простейшие уравнения (п.4).

5: Идемпотентность.

х  х = х, х  М.

Вообще-то количество одинаковых элементов в выражении может быть любым. Идемпотентность позволяет в необходимых случаях сжимать или, наоборот, растягивать выражение. То же, кстати, было и в алгебре логике для операций дизъюнкция и конъюнкция.

6: Дистрибутивность.

Здесь уже требуются две операции, обозначаемые, например,  (операция типа умножение) и  (операция типа сложение).

Дистрибутивность  по отношению к :

х  (у  z) = (х  у)  (х  z),

(х  у)  z= (х  z)  (у  z),

x, y, z  M.

Здесь второе равенство также необходимо, поскольку дистрибутивность рассматривается независимо от коммутативности.

Аналогично выглядит и вторая дистрибутивность:  относительно .

Кстати, в обычной алгебре умножение дистрибутивно относительно сложения:

a (b + c) = a b + a c,

но не наоборот:

a + b c  (a + b) (a + c).

Последнее условие может быть неверно только в частном случае (например, b = с = 0, а = 1).

Другие свойства операций (7, …) пока не рассматриваем.

Предложение 1.

Если единица операции существует, то она единственная.

Доказательство проводится «от противного». Пусть, наоборот, существуют две различные единицы e₁ и e₂.

Тогда справедливо

e₁  e₂ = e₁,

поскольку e₂ – единица.

Аналогично,

e₁  e₂ = e₂,

Поскольку e₁ – единица.

В итоге получается e₁ = e₂, т. е. противоречие исходному предположению о различных e₁ и e_2.

Предложение 2.

Операция  на множестве М ассоциативна, имеет единицу и обратный элемент. Этот обратный элемент (по отношению к некоторому элементу х) – единственный.

Доказательство от противного: два обратных элемента х₁  х₂.

Тогда

х  х₁ = х₁  х = е,

х  х₂ = х₂  х = е.

Получаем

х = х₁  е (свойство единица) = х₁  (х х₂) = = (х₁  х)  х₂ (ассоциативность) = е  х₂ = х₂ (единица).

Пришли к противоречию: х₁ = х₂.
Лекция 15. Понятие вычета по модулю N. Операции над вычетами. Шифрование.
Понятие вычета.

Вычетом числа a по модулюm называется остаток от деления a на m

Из определения видно, что вычеты связаны с делением с остатком.

Разделить натуральное число aна нату­ральное число b с остатком означает yнайти неотрицательные числа два числа q и г, причем г < b такие, что выполняется равенство

а = q·b + г

Так для чисел 187 и 12 соответствуют два числа 15 и 7, такие, что 187= 15·12+7. Это равенство часто записывается в виде 187:12 = 15(ост. 7).

Напишем названия компонентов деления с остатком:

а – делимое, b- делитель, q- частное, r – остаток.

Рассмотрим еще примеры:

а = - 12, b = 8 ® -12 = (- 2) · 8 + 4, q= -2, r=4

а = - 324, b = - 15 ® - 324 = 22 · (- 15) + 6 q=22, r=6

a = 4, b=10 ® 4=0·10+4 q=0, r=4

a = 12, b = 4 ® 12=4·3+0 q=4, r=0

Число aделится нацело на b, если остаток r = 0 или, а = qb. .Причем отношение "делиться на цело" обозначается .

Теорема. Если а и bделятся на с, то при любых целых kи j сумма ka + jbделится на с.

Пример. Найти такое число d¹1, на которое делятся чис­ла 6п + 5 и 9л + 2. При каком значении п. это деление возможно?

Решение. Если числа 6п + 5 и 9п + 2 делятся на d, то на dделится и разность

3(6n + 5) - 2(9п + 2) = 15 - 4 = 11

Число 11 - простое число, значит d= 11.

Не трудно установить, что п = ...- 21, - 10, 1, 12, 23...

Сравнение по модулю.

Числа в основном сравнивают по величине, но их можно сравнивать по другим признакам и свойствам. Например, по количеству цифр, по остаткам деления, по делимости на некоторое число и др.

Рассмотрим сравнение чисел на основе равенства их остатков при делении на некоторое число, что приводи к понятию вычетов. Такое сравнение называется сравнением по модулю. Не следует путать с абсолютной величиной числа, которая так же называется модулем. Введем форму записи остатка:

R = A mod B, где A-делимое, B- делитель, R-остаток.

Получаемое в процессе деления частное в данном случае не рассматривается.

Например, 5=15 mod 10, 3= 45 mod 7 и т.д.

При делении n ("nÎZ) на gвсе целые числа разбиваются на gподмножеств, которые соответствуют числу, полученному в остатке. Остатки при этом будут равны:

n mod g ={0,1,2,…g-1}

Причем, каждому остатку можно поставить в соответствие множество чисел вида:

0 ® n mod g =0 n=k g

1 ® n mod g =1 n=kg+1

2 ® n mod g =2 n=kg+2

3 ® n mod g =3 n=kg+3

g-1 ® n mod g =g-1 n=k(g-1)

Очевидно, что любое целое число а принадлежит одному из этих g подмножеств. Причем разность любых двух чисел одного под­множества делится на g, а разность чисел из разных множеств не должна делиться на g.

Два целых числа называются сравнимыми по модулю g (g ³ 2), если их разность кратна натуральному числу, т.е. (а - b) g,.

Запишем это определение символами:

а º b (mod g), если $ kÎ Z (а - b= kg).,

Это значит, что числа а и b сравнимы по модулю g тогда и только тогда, когда они принадлежат одному подмножеству, т.е. дают одинаковые остатки при делении на g..

Например: 36 º I6 (mod l0) – числа 36 и 16 сравнимы по модулю 10

24 º 4 (mod 6) - число 24 сравнимо по модулю 6 с число 4

-26º 6 (mod 30)

Отметим разницу в записях: записей:

1. аº b (mod g ) или (а= b) (mod g ) означает сравнимость чисел по модулю (сравнение)

2. а= b (mod g ) - означает равенство числа a остатку от деления b на g

Отношение сравнимости рефлексивно, симметрично, транзитивно. Следовательно, оно является отношением эквивалентности.

Вычетами по модулю р называют отдельные классы эквивалентности для отношения сравнимо­сти (по модулю p)) и обозначают Z_p,

Раздел математики, изучающий вычеты по модулю, называется ал­геброй вычетов (теорией вычетов, модулярной арифметикой).

Свойства сравнимости

1. Два числа, сравнимые с третьим по одному модулю, сравни­мы между собой:

2. Сравнения можно складывать и вычитать:

(а º b(mod p); cºd(mod p)) => (а ± с) º (b ± d)(mod p).

Слагаемые можно переносить из одной части сравне­ния в другую с противоположным знаком.

3. Сравнения можно перемножать:

(a º b(mod p), с º d(mod p)) => (ас º bd(mod p)).

4. Обе части сравнения можно умножить на одно и то же целое число k:

(а º 6(mod p}) => (ak º bk(mod p)).

5. Обе части сравнения и модуль можно умножить на одно и то же число:

(а º b (mod p)) => (akºbk(mod pk)).

6. Обе части сравнения можно возвести в степень (следствие свойства 3):

(а º b (mod p)) => (аⁿ = bⁿ (mod p)).

Понятие сравнения ввел К.Ф.Гаусс в работе "Ариф­метические исследования" (1802). Алгебра вычетов возникает в тех случаях, когда рассматриваются некоторые циклически повторя­ющиеся события, например время в течение дня, повторяющееся каждые 24 часа, углы по окружности, повторяющиеся через пе­риод 2к, и т.д.

Алгебра вычетов - один из тех разделов математики, которые рождались как некоторые формальные рассуждения и только спустя годы нашли свое практи­ческое применение.

Пример. Для степени y=2ⁿ (n–натуральное число) установить классы сравнимости. Установить зависимость последней цифры этой степени от ее показателя.

Решение и комментарии.

Как известно, натуральные степени числа 2 оканчиваются циф­рами {2, 4, 8, 6}. См. таблицу нескольких степеней числа 2.

Опреде­лим функцию, которая ставит в соответствие каждому натуральному числу п последнюю цифру числа 2^я:

n	2n	Последняя цифра 2т
1	2	2
2	4	4
3	8	8
4	16	6
5	32	2
6	64	4
7	128	8
8	256	6

f: N®{2, 4, 8, 6},

Эта функция f(n) периодична с периодом 4. Это значит, что для целого числа k: f(n)=f(n+4)= f(n+4k),.

Причем справедливы так же равенства: f(n)=f(n-4)= f(n-4k)

Последнее равенство означают, что для любого п нужно найти минимальное натуральное т, такое, что f(m) = f(m + 4k) = f(n).

Но это задача на делении с остатком числа n на 4:

n=4k+m, k-частное, т - остаток.

Очевидно, последняя цифра числа 2" зависит от остатка, полученного при делении показателя n степени 2 ⁿ на 4.

Отразим этот факт в записи функции: f(n)= f(n mod 4)

Из этой формулы можно установить, если f(n mod 4)=0, то

При делении чисел на 4 "nÎN, останки могут быть: 0,1,2,3. Таким образом, в частности, множество всех возможных показателей степени 2 ⁿ для любого n состоит из четырех подмножеств: 4k, 4k+ 1, 4k+ 2, 4k+3.

Пример. Установить последнюю цифру степени y=2 ²⁰⁰⁷

Решение. Имеем 2007=501·4+3, значит f (2007)=f (3)=2³=8. Ответ
Лекция 16. Метод математической индукции
Метод математической индукции - не просто распространенный метод решения олимпиадных задач, но и способ доказательства многих утверждений в математической науке. (Не случайно эта лекция такая длинная!) Поэтому знать этот метод нужно не только математику-олимпиаднику, но и каждому, кто собирается в дальнейшем изучать высшую математику или теорию алгоритмов. Что же такое индукция?

Часто индукцию сравнивают с падением ряда доминошек: мы толкаем первую доминошку - она падает и задевает вторую. Вторая доминошка от этого тоже падает и задевает третью. Теперь падает третья доминошка, задевает четвертую... - и в итоге падает весь ряд. А происходит это по двум причинам:
1.) Мы толкаем первую доминошку.

2.) Любая доминошка, падая, задевает следующую.

Доказательство по индукции протекает аналогичным образом. У нас есть ряд утверждений (обычно - бесконечно длинный), которые надо доказать. И для этого достаточно доказать всего два утверждения:

1.) База индукции: первое утверждение ряда верно.

2.) Переход индукции: если верно какое-то утверждение ряда (неважно, какое именно), то верно и следующее за ним утверждение ряда. (эти два пункта аналогичны пунктам про падающие доминошки!)

Почему же тогда верны все утверждения ряда? Первое утверждение верно по базе индукции. По переходу индукции мы получаем, что если верно первое утверждение ряда, то верно и второе. Значит, верно и второе утверждение. Еще раз применяем переход: если верно второе утверждение, то верно и третье. Значит, третье утверждение тоже верно. Сделав еще один такой шаг, мы получим, что вернои четвертое утверждение. Затем - пятое, шестое... десятое... сотое... тысячное... миллионное... В общем, верно утверждение ряда со сколь угодно большим номером, то есть любое, то есть каждое - что и требовалось доказать.
Такой ряд утверждений, где у каждого утверждения есть свой порядковый номер ("первое", "второе" и т.п.) по-научному называется "ряд утверждений, занумерованных натуральными числами". И факт наличия в задаче такого ряда следует понимать весьма творчески. Часто имеется одно утверждение (У), но в нем есть какой-то параметр (например, n), являющийся натуральным числом. Тогда первое утверждение ряда (У₁) - это утверждение У при n=1. Второе утверждение ряда (У₂) - это утверждение У при n=2... сотое (У₁₀₀) - это утверждение У при n=100 и т.д. Часто утверждение У - это тождество с одной натуральной переменной (иногда и с несколькими - но об этом ниже). Иногда в задаче просят доказать только одно конкретное утверждение ряда (например, У₅, У₇ или У₁₀) - но это нельзя сделать проще, чем доказать весь ряд по индукции (см. примеры ниже).

Пример. Из квадрата 16x16 клеток вырезали одну клетку. Докажите, что полученную фигуру можно разрезать на уголки из трех клеток.
Решение № 1. Что делать, если не хочется рассматривать кучу разных случаев вырезания клетки из квадрата 16x16 (как ни сокращай, но 36 принципиально разных случаев там есть)? Давайте посмотрим на квадраты поменьше (но тоже со стороной, равной степени двойки): 8x8, 4x4, 2x2. Для 2x2 доказывать нечего: вырезали любую клетку, и остался один уголок. А вот теперь посмотрим на квадрат 4x4 - он составлен из 4-х квадратов 2x2 (см. рис.). В один из них попадет вырезанная клетка (черная на рис.) - и он разрежется на уголки (т.е., как сказано выше, там будет ровно 1 уголок). Что же делать с тремя другими? (это и есть самый сложный для момент в задаче!) А давайте возьмем в этих трех квадратах уголок, прилежащий к центру большого квадрата - и отрежем его (серые клетки на рис.). Тогда у нас останется три квадратика 2x2 с вырезанной клеткой - а их мы уже умеем разрезать на уголки.



Теперь перейдем от 4x4 к 8x8: квадратик 8x8 составен из четырех квадратиков 4x4. В одном из них есть вырезанная клетка, а в остальных трех мы вырежем по клетке, отрезав прилежащий к центру уголок (аналогично предыдущему). Теперь образуется 4 квадратика 4x4, в каждом из которых вырезана клетка. Каждый из них мы умеем разрезать на уголки - значит, разрежем и весь квадрат 8x8. А от квадрата 8x8 можно точно так же перейти к квадрату 16x16, составив его из четырех частей - получаем ч.т.д (пример разрезания всего квадрата 16x16 на уголки - см. рис. внизу).



Решение №2. (то же самое, но с волшебным словом "индукция") Докажем по индукции следующее утверждение: квадрат 2ⁿx2ⁿ с одной вырезанной клеткой можно разрезать на уголки из трех клеток.(На самом деле, здесь спрятан бесконечный ряд утверждений: про квадрат 2x2, 4x4, 8x8, 16x16... 1024x1024 и т.д.)
База: Квадрат 2x2 с одной вырезанной клеткой можно разрезать на уголки. Это верно, т.к. после вырезания клетки от квадрата 2x2 остается один уголок.
Переход: Если квадрат 2ⁿx2ⁿ с одной вырезанной клеткой можно разрезать на уголки, то можно разрезать и квадрат 2ⁿ⁺¹x2ⁿ⁺¹. Действительно, квадрат 2ⁿ⁺¹x2ⁿ⁺¹ составлен из четырех квадратов 2ⁿx2ⁿ. В одном из них вырезана клетка, а в остальных трех квадратах вырежем по клетке, отрезав уголок, прилежащий к центру исходного квадрата. Тогда каждый из этих четырех квадратов можно будет разрезать на уголки по предположению индукции, значит, можно разрезать и исходный квадрат, ч.т.д.

Замечание: предположением индукции называется предположение о верности очередного утверждения ряда, из верности которого мы в переходе индукции доказываем верность следующего утверждения ряда.

(!) Когда задача решается по индукции, то решение записывается в стиле, похожем на решение №2. Но придумывается оно часто в стиле решения №1 - так бывает удобнее, особенно для начинающих ;-)
А настоящее овладение методом- это умение придумывать решение сразу таким, как оно будет записано ;-)

Пример. Докажите, что число из 243 единиц делится на 243.
Решение №1: Давайте опять попробуем что-нибудь попроще. Например, 111 делится на 3, а число 111111111 - на 9. Это, конечно, правда, по общеизвестным признакам делимости на 3 и на 9 (на 3 и на 9 делится сумма цифр этих чисел). Но дальше признаки делимости заканчиваются :(Что же делать? Давайте по-другому докажем, что 111111111 делится на 9 - так, чтобы можно было из этого сделать переход в общем виде. Конечно, надо пользоваться тем, что в общем виде будет предположением индукции: 111 делится на 3. А давайте 111111111 на него поделим - в частном будет 1001001. Это частное, конечно, делится на 3 (по тому же признаку). А произведение двух чисел, делящихся на 3, делится на 9.
Идем дальше: почему число из 27 единиц делится на 27? Поделим его на 111111111 и получим в частном 10¹⁸+10⁹+1. Это частное опять делится на 3 (его сумма цифр 3), а делитель, как мы уже знаем, на 9. Поэтому число из 27 единиц делится на 9*3=27. Само это число будет делителем числа из 81 единицы, и в частном получается уже 10⁵⁴+10²⁷+1 - все равно оно на 3 делится, по тем же причинам. А число из 81 единицы поделится тогда на 27*3=81, что и следовало ожидать. Еще один такой же переход - и мы получим, что число из 243 единиц делится на 243, ч.т.д.
(!) Важная мысль: здесь, переходя к предыдущим шагам, мы уменьшаем уже не один, а оба параметра: число, которое должно делится, и число, на которое оно должно делится.

Решение №2: (опять то же самое, но сторого индуктивно записанное) Докажем по индукции утверждение: число из 3ⁿ единиц делится на 3ⁿ (т.е. бесконечный ряд утверждений при разных натуральных n).

База: 111 делится на 3 (n=1). Святая правда. В частном 37 получается.
Переход: Заметим, что число из 3ⁿ⁺¹ единиц делится на число из 3ⁿ единиц, и в частном будет 10^2*3n+10³ⁿ+1 (т.е. число из трех единиц и кучи нулей). Делитель, по предположению индукции, делится на 3ⁿ, а частное - на 3 (т.к. его сумма цифр 3). Значит, число из 3ⁿ⁺¹ единиц делится на 3ⁿ*3=3ⁿ⁺¹, ч.т.д.
Замечание: Можно доказать, опять же по индукции, что число из 3ⁿ единиц содержит 3 в степени ровно n. При n=1 это верно (база), а дальше заметим, что частное от деления числа из 3ⁿ⁺¹ единиц на число из 3ⁿ единиц делится только на 3, но не на 9, т.к. его сумма цифр равна 3 (переход).

Мы заметили некоторую закономерность в значениях изучаемой последовательности. Проверяем эту закономерность для n=1. Предполагаем, что формула справедлива при некотором n и доказываем, что она справедлива для n=n+1. Подставляем в формулу n+1 и получаем формулу, которой соответствует (n+1) – ый член. Затем получаем (n+1) – ый член, исходя из общего принципа построения последовательности. Получим формулу для n+1. Если эти формулы совпадают, то закономерность считается доказанной.

Пример:

S , при n=1 эта формула справедлива: Пусть она справедлива при некотором n. Если она справедлива для n+1, то должно быть S .

Получим эту формулу из общих соображений.

S_n+1 = S_n + n +1 = + n+1 = (n+1) ( +1) =

Что и требовалось доказать.

Пример. Докажите, что 1+2+...+N=N(N+1)/2 (такие числа называются "треугольными": 1, 3, 6, 10, 15, 21, 28...).

Решение: Докажем по индукции (обычно говорят "докажем индукцией по N", т.е. по переменной, значением которой нумеруются утверждения в ряду).
База: N=1 - и действительно, 1=1(1+1)/2.

Переход: Пусть тождество верно для какого-то значения N, которое мы теперь тоже обозначим за N. Надо доказать, что оно верно и для значения, на 1 большего, т.е. (в новом смысле буквы N) для N+1. Теперь предположение индукции будет выглядеть, как 1+2+...+N=N(N+1)/2, а то, что надо доказать - как результат подстановки сюда N+1 вместо N, т.е. 1+2+...+N+(N+1)=(N+1)(N+2)/2.

Техническая часть - из одного равенства вывести другое - трудностей не представляет: 1+2+...+N+(N+1) = N(N+1)/2+(N+1) - по предположению индукции (т.е. по первому равенству). А это равно (N+1)(N/2+1) = (N+1)(N+2)/2, ч.т.д.

Пример. Докажите, что 1+3+...+(2N-1)=N² - сумма первых N нечетных чисел равна N².
Решение: Докажем индукцией по N, но теперь эту идейную подтасовку будет опускать.
База: N=1 - действительно, 1=1².

Переход: Предположение индукции: 1+3+...+(2N-1)=N² - так и пишут в индуктивных доказательствах, скрывая ту подтасовку, которая была продемонстрирована в решении предыдущей задаче (и сбивая с толку тех, кто плохо понимает метод индукции!). Утверждение, которое надо доказать: 1+3+...+(2N-1)+(2*(N+1)-1) = (N+1)² - т.е. 1+3+...+(2N-1)+(2N+1) = (N+1)². Его левая часть, по предположению индукции - это N²+2N+1, что, конечно же, равно (N+1)², ч.т.д.

Пример. Докажите, что 2^N>N при любом натуральном N.
Решение: Докажем индукцией по N (и тут, и далее в переходе применяется все та же идейная подтасовка!).

База: N=1 - действительно, 2¹=2>1.

Переход: Предположим, что при некотором N 2^N>N. Теперь докажем, что 2^N+1>N+1. Действительно, 2^N+1=2*2^N>2N по предположению. А 2N>=N+1 при всех N (очевидно), откуда 2^N+1>N+1, ч.т.д.

Доказательство делимости по индукции мы уже видели в задаче 2. Вот еще один типичный пример:

Пример. Докажите, что 3^2N+2+8N-9 делится на 16 при любом натуральном N.
Решение: Докажем индукцией по N.

База: N=1 - действительно, 3^2*1+2+8*1-9=80 - делится на 16.

Переход: Уже известная махинация сводит доказательство перехода к следующему утверждению: если 3^2N+2+8N-9 делится на 16, то 3^2(N+1)+2+8(N+1)-9 делится на 16. Последнее число равно 3^2N+4+8N+8-9 = 9*3^2N+2+8N+8-9 = 8*3^2N+2+3^2N+2+8N+8-9 = 8*(3^2N+2+1)+3^2N+2+8N-9 Сумма последних трех слагаемых делится на 16 по предположению, а первое - как произведение 8 и четного числа 3^2N+2+1, ч.т.д.

Лекция 17. Генерирование К-элементных подмножеств данного множества
Существует набор задач, решение которых заключается в генерации всех элементов таких комбинаторных объектов как множество всех подмножеств, перестановки, сочетания, размещения, перестановки с повторениями, сочетания с повторениями.

Для каждого сгенерированного элемента затем проверяются какие-то свойства для конкретной задачи. Задачи, в которых требуется определить количество возможных операций, называется комбинаторными. Пусть имеется группа некоторых объектов , , которые мы будем называть элементами.

Из этой группы элементов будем образовывать подгруппы. Такие подгруппы будем называть соединениями.

Из этих соединений выделим классы, которые будем называть размещениями.