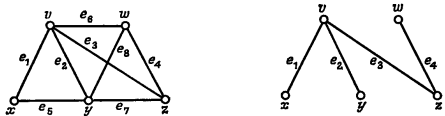Смежность и инцидентность
Пусть v1, v2 - вершины, е = (v1, v2) - соединяющее их ребро. Тогда вершина v1 и ребро е инцидентны, вершина v2 и ребро е также инцидентны. Два ребра, инцидентные одной вершине, называются смежными; две вершины, инцидентные одному ребру, также называются смежными.
Степенью вершины v графа G(V,E) называется число ребер, инцидентных данной вершине. Обозначение: 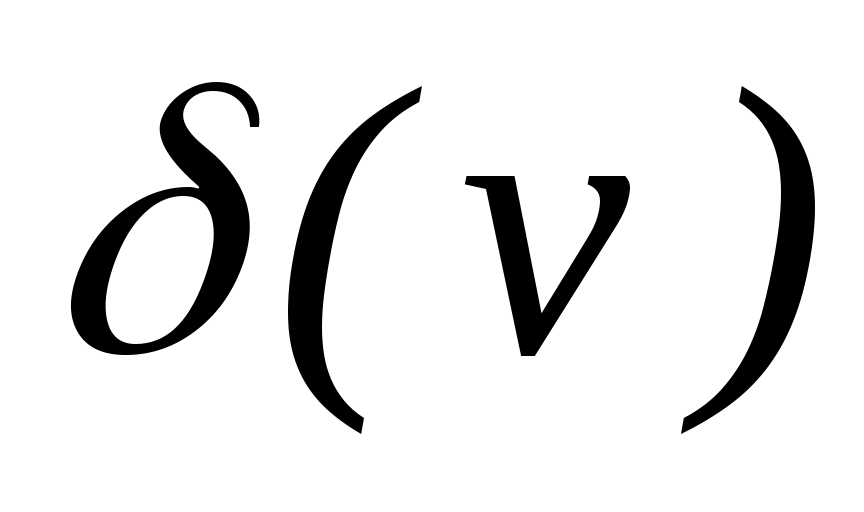 . .
Вершина, имеющая степень 0 называется изолированной, имеющая степень 1 – висячей.
Пример. Для графа, изображенного на рис. 3: вершина 3 – изолированная, вершины 1 и 4 - висячие.
Пример. Для графа, изображенного на рис. 1.
Ребро e1 инцидентно вершинам v1 и v2. Вершина v1 инцидентна ребрам e1 и e2. Ребра e1 и e2 – смежны. Вершины v1 и v2 – смежны.
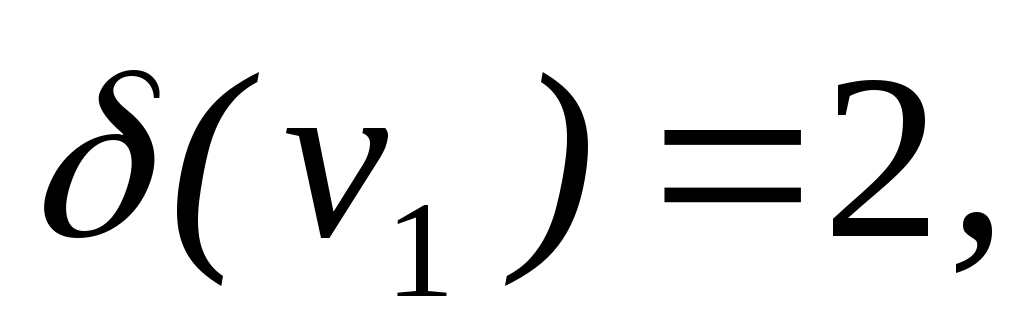 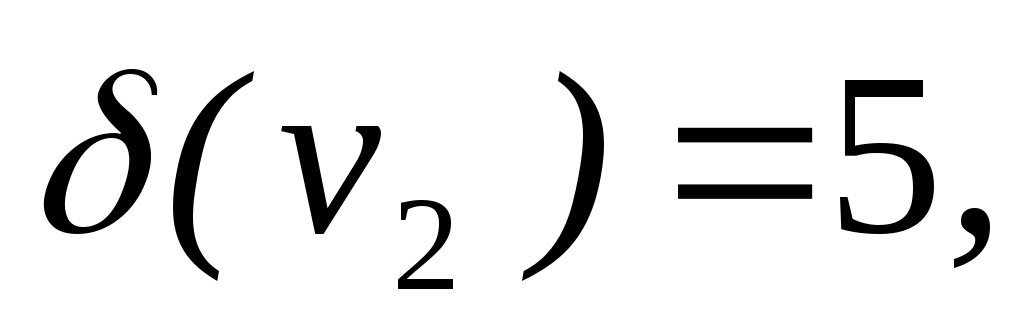 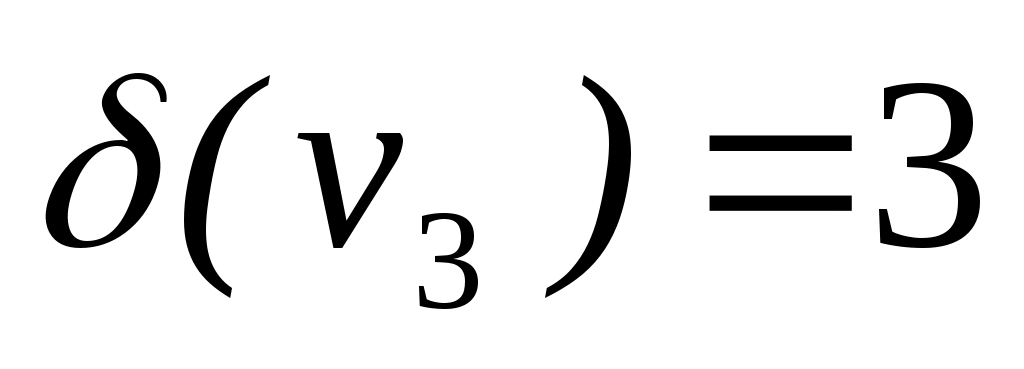 . p(G)=3, q(G)=5. . p(G)=3, q(G)=5.
Т.о. можно заметить, что 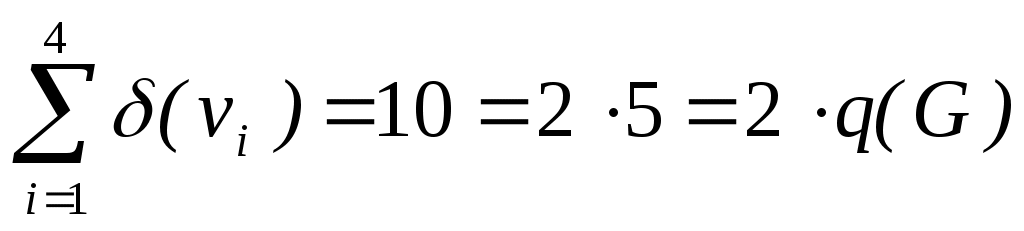 . .
Теорема Эйлера:  . .
Доказательство данной теоремы вытекает из того, что каждое ребро дает двойной вклад в сумму степеней вершин.
Лекция 19. Изоморфные графы. Эйлеровы графы.
Изоморфизм графов
Говорят, что два графа G1(V1,E1) и G2(V2,E2) изоморфны (обозначается G1
G2), если существует биекция h: V1 V2, сохраняющая смежность. V2, сохраняющая смежность.
Графы рассматриваются с точностью до изоморфизма.
Пример
Три внешне различные диаграммы, приведенные на рис. 1, являются диаграммами одного и того же графа К3,3.
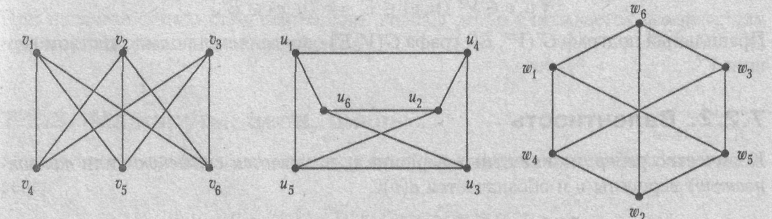
Рис. 1. Диаграммы изоморфных графов
Числовая характеристика, одинаковая для всех изоморфных графов, называется инвариантом графа. Так, p(G) и q(G) - инварианты графа G.
Не известно никакого набора инвариантов, определяющих граф с точностью до изоморфизма.

Рис. 2. Диаграммы неизоморфных графов с совпадающими инвариантами
Требования к представлению графов
Известны различные способы представления графов в памяти компьютера, которые различаются объемом занимаемой памяти и скоростью выполнения операций над графами.
Представление выбирается, исходя из потребностей конкретной задачи. Далее приведены два из наиболее часто используемых представления.
Указанные представления пригодны для графов и орграфов, а после некоторой модификации также и для псевдографов, мультиграфов.
Представления иллюстрируются на конкретных примерах графа G и орграфа D, диаграммы которых представлены на рис.3.
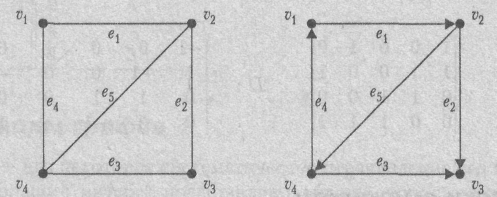
Рис. 3. Диаграммы графа (слева) и орграфа (справа), используемых в качестве примеров
Эйлеровы графы Вернемся к историческому примеру о Кенигсбергских мостах. В каком случае в графе можно найти цикл, в котором каждое ребро участвует ровно один раз?
Цикл, содержащий каждое ребро ровно один раз, называется эйлеровым. Граф, содержащий эйлеровый цикл, называется эйлеровым графом.
Теорема (критерий эйлеровости графа): конечный граф G(V,E) является эйлеровым, тогда и только тогда, когда он связен и степени всех его вершин – четны.
Цепь, содержащая каждое ребро ровно один раз, называется эйлеровой. Граф, содержащий эйлерову цепь, называется полуэйлеровым графом.
Теорема (критерий полуйлеровости графа): конечный граф G(V,E) является полуэйлеровым, тогда и только тогда, когда он связен и точно две го вершины имеют нечетную степень.
Лекция 20. Плоские графы. Деревья и их свойства
Важным частным случаем ориентированнных ациклических графов являются деревья. Класс деревьев занимает в теории графов особое положение. С одной стороны, это достаточно просто устроенные графы, и многие задачи, весьма сложные в общей ситуации, для деревьев решаются легко. С другой стороны, деревья часто встречаются в областях, на первый взгляд не имеющих отношения к теории графов.
Деревом называется связный граф, не содержащий циклов. Любой граф без циклов называется ациклическим (или лесом). Таким образом, компонентами леса являются деревья. На рисунке 1 изображены все деревья шестого порядка.
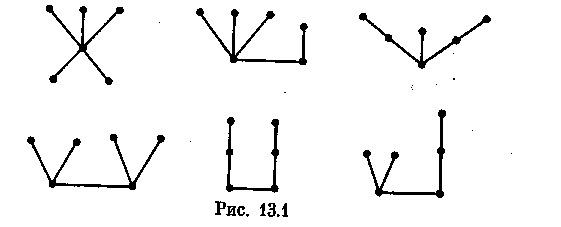
Рис. 1 Деревья шестого порядка.
В следующей теореме перечислены некоторые простые свойства деревьев.
Теорема. Пусть граф Т имеет n вершин. Тогда следующие утверждения эквивалентны: (i) Т является деревом; (ii) Т не содержит циклов и имеет n — I ребер; (iii) Т связен и имеет n — 1 ребер; (iv) Т связен и каждое его ребро является мостом; (v) любые две вершины графа Т соединены ровно одной простой цепью; (vi) Т не содержит циклов, но, добавляя к нему любое новое ребро, мы получаем ровно один цикл.
Доказательство. Если n = 1, утверждение очевидно. Предположим поэтому, что п> 2.
(i) =>(ii). По определению Т не содержит циклов; тогда удаление любого ребра разбивает Т на два графа, каждый из которых является деревом. По индуктивному предположению число ребер в каждом из этих деревьев на единицу меньше числа вершин. Отсюда выводим, что полное число ребер графа Т равно n — 1.
(ii) => (iii). Если граф Т несвязен, то каждая его компонента представляет собой связный граф без циклов. Из предыдущей части доказательства следует, что число вершин в каждой из компонент больше числа ее ребер на единицу. Значит, полное число вершин графа Т больше полного числа его ребер по крайней мере на 2, а это противоречит тому, что Т имеет n — 1 ребер.
(iii) => (iv). Удаление любого ребра приводит к графу с n вершинами и n — 2 ребрами, который не может быть связным.
(iv) =>(v). Так как Т связен, то каждая пара его вершин соединена по крайней мере одной простой цепью. Если же данная пара вершин соединена двумя простыми цепями, то они замыкаются в цикл, а это противоречит тому, что каждое ребро в Т является мостом.
(v)=>(vi). Если T содержит цикл, то любые две вершины этого цикла соединены по крайней мере двумя простыми цепями. Добавим теперь к графу Т какое-то ребро е. Тогда мы получим цикл, поскольку инцидентные ребру е вершиныуже соединены в Т простой цепью.
(vi)=>(i). Предположим, что Т несвязен; тогда добавление любого ребра, соединяющего вершину одной компоненты с вершиной другой компоненты, не приводит к образованию цикла. ▪
Следствие. Пусть G — лес с п вершинами и k компонентами; тогда G имеет п — k ребер.
Доказательство. Применим к каждой компоненте графа G предложение (ii) теоремы 1. ▪
Заметим, что по лемме о рукопожатиях сумма степеней всех n вершин дерева равна удвоенному числу его ребер(2n — 2); отсюда следует, что при n> 2 дерево, имеющее n вершин, всегда содержит не менее двух висячих вершин. Известно, что в связном графе G удаление одного ребра, принадлежащего некоторому выбранному циклу, не нарушает связности оставшегося графа. Применим эту процедуру к одному из оставшихся циклов, и так до тех пор, пока не останется ни одного цикла. В результате получим дерево, связывающее все вершины графа G; оно называется остовным деревом(или остовом, каркасом) графа G. Пример графа и одного из его остовных деревьев дан на рисунке 2.
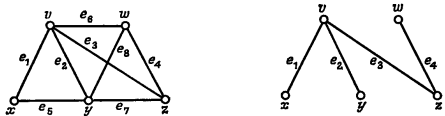
Рис. 2. Граф и одно из его остовных деревьев
В общем случае обозначим через G произвольный граф с n вершинами, m ребрами и k компонентами. Применяя описанную выше процедуру к каждой компоненте G, получим в результате граф, называемый остовным лесом. Число удаленных в этой процедуре ребер называется циклическим рангом (или цикломатическим числом) графа G и обозначается через γ(G). Очевидно, что γ (G) = m — n + k и является неотрицательным целым числом.
Таким образом, циклический ранг дает меру связности графа: циклический ранг дерева равен нулю, а циклический ранг циклического графа равен единице, удобно также определить коциклический ранг (или ранг разреза) графа G как число ребер в его остовном лесе; коциклический ранг обозначается через χ(G) и равен n — k.
Докажем два простых результата, касающихся остовных лесов. В этой теореме дополнением остовного леса Т некоторого (необязательно простого) графа G является граф, полученный из G удалением ребер Т.
Теорема 3. Если Т — остовный лес графа G, то (i) всякий разрез в G имеет общее ребро с Т; (ii) каждый цикл в G имеет общее ребро с дополнением Т.
Доказательство. (i) Пусть С* — разрез графа G, удаление которого разбивает одну из компонент G на два подграфа H и К. Поскольку Т — остовный лес, в нем должно содержаться ребро, соединяющее вершину из H с вершиной из К; это и есть требуемое ребро.
(ii) Пусть С — цикл в графе G, не имеющий ни одного общего ребра с дополнением Т; тогда С содержится в Т, что невозможно. ▪
C понятием остовного леса 7 графа О тесно связано понятие фундаментальной системы циклов, ассоциированной с Т. Оно определяется следующим образом: если добавить к Т любое не содержащееся в нем ребро графа G , то по предложению (vi) теоремы 1 получим единственный цикл; множество всех циклов, получаемых таким способом (т. е. путем добавления по отдельности каждого ребра из G, не содержащегося в Т), называется фундаментальной системой циклов, ассоциированной с T. В том случае, когда нас не интересует, какой остовный лес рассматривается, мы говорим о фундаментальной системе циклов графа G. Ясно, что циклы данной фундаментальной системы должны быть различными и что их число должно равняться циклическому рангу графа G. На рисунке 3 показана фундаментальная система циклов графа ассоциированная с остовным деревом:
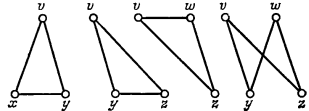
Рис. 3. Фундаментальная система циклов графа ассоциированная с остовным деревом:
Можно определить фундаментальную систему разрезов графа G, ассоциированную с данным остовным лесом Т. Покажем, что это действительно можно сделать. По предложению (iv) теоремы 1 удаление любого ребра из Т разбивает множество вершин дерева Т на два непересекающихся подмножества V1 и V2. Множество всех ребер графа G, каждое из которых соединяет вершину из V1 с вершиной из V2, является разрезом графа G. Множество всех разрезов, полученных таким способом (т. е. удалением по отдельности каждого ребра из Т), называется фундаментальной системой разрезов, ассоциированной с Т. Ясно, что разрезы данной фундаментальной системы должны быть различными и что их число должно равняться коциклическому рангу графа G. Фундаментальной системой разрезов графа, изображенного на рис., ассоциированной с остовным деревом, изображенным на рис, является такая система: {e1, е5}, {е2 ,е5, е7 ,е8}, {е3, е6, е7, е8} и {е4, е6, е8}.
Лекция 21. Понятие ориентированного графа
Орграфом D называется пара (V(D), A(D)), где V(D) - непустое конечное множество элементов, называемых вершинами, и A(D) - конечное семейство упорядоченных пар элементов из V(D), называемых дугами; V(D) и A(D) называются соответственно множеством вершин и семейством дуг орграфа D. Так, на рис. 1 представлен орграф, дугами которого являются (u, v), (v, v), (v, w), (v, w), (w, v), (w, u) и (z, w); порядок вершин на дуге указан стрелкой.
Граф, полученный из орграфа D «удалением стрелок» (т.е. заменой каждой дуги вида (v, w) на соответствующее ребро {v,w}), называется основанием орграфа D (рис. 2).
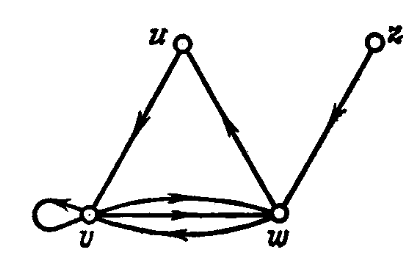
Рис. 1 Орграф
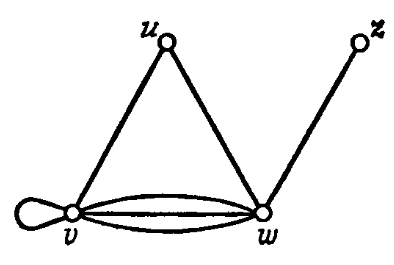
Рис. 2. Основание орграфа
Две вершины v и w орграфа D называются смежными, если в A(D) существует дуга вида (v, w) или (w, v); при этом вершины v и w называются инцидентными любой такой дуге (а дуга — инцидентной соответствующим вершинам).
Два орграфа называются изоморфными, если существует изоморфизм между их основаниями, сохраняющий порядок вершин на каждой дуге. Матрицей смежности орграфаG множеством вершин {v1,…, vn} является матрица А = (aij), в которой aij равно числу дуг вида (vi, vj) в семействе A(D). Матрица, показанная на рис.3, является матрицей смежности для орграфа, изображенного на рис. 1. Простой орграф определяется очевидным образом.
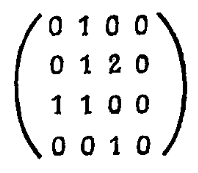
Рис. 1 Матрица смежности
Ориентированный маршрут в орграфе D представляет собой конечную последовательность дуг вида (v0, vj, (vl, v2), vm). Можно записывать эту последовательность в виде v0 ->v1 ->... ->vm и говорить об ориентированном маршруте из v0 в vm. Аналогичным образом можно определить ориентированные цепи, ориентированные простые цепи и ориентированные циклы, или орцепи, простые орцепи и орциклы.
Заметим, что хотя орцепь не может содержать данную дугу (v, w) более одного раза, она может содержать одновременно (v, w) и (w, v); например, на рис. 1 z ->w ->v ->w ->u является орцепью. Теперь мы в состоянии определить связность. Точнее, мы определим здесь два наиболее естественных и полезных типа связности орграфов, которые возникают в соответствии с тем, хотим мы или нет принимать во внимание ориентацию дуг.
Говорят, что орграф Dсвязен (или слабо связен), если он не может быть представлен в виде объединения двух различных орграфов (определенного обычным образом); это эквивалентно тому, что связно основание орграфа D. Предположим дополнительно, что для любых двух вершин v и w орграфа D существует простаяорцепь из v в w; тогда D называется сильно связным (этот термин настолько устоялся, что мы использовали его вместо более естественного «орсвязный»). Ясно, что любой сильно связный граф связен, но обратное неверно: на рис. 1 изображен связный орграф, не являющийся сильно связным.
Различие между связным и сильно связным орграфом станет яснее, если мы рассмотрим план города, по всем улицам которого допускается только одностороннее движение. Тогда связность соответствующего орграфа означает, что мы можем проехать из любой части города в любую другую, не обращая внимания на правила одностороннего движения; если же этот орграф сильно связен, то мы можем проехать из любой части города в любую другую, следуя всегда «правильным путем» вдоль улиц с односторонним движением. Важно, чтобы система с односторонним движением была сильно связной, и естественно возникает вопрос: при каких условиях карту улиц можно превратить в систему с односторонним движением таким способом, чтобы можно было проехать из любой части города в любую другую? Если, к примеру, город состоит из двух частей, связанных одним мостом, то мы никогда не сможем сделать все его улицы односторонними, поскольку какое бы направление мы ни приписали мосту, одна часть города будет отрезана. (Заметим, что сюда включается и тот случай, когда в городе имеется тупик.) С другой стороны, если мостов нет, то всегда найдется подходящая односторонняя система.
Для удобства будем называть граф G ориентируемым, если каждое его ребро (рассматриваемое как пара вершин) может быть упорядочено таким образом, что полученный в результате орграф будет сильно связным. Этот процесс упорядочения ребер будем называть «заданием ориентации графа» или «приписыванием направлений ребрам». Если, например, G - граф, изображенный на рис. 4, то его можно ориентировать и получить сильно связный орграф, изображенный на рис. 5.
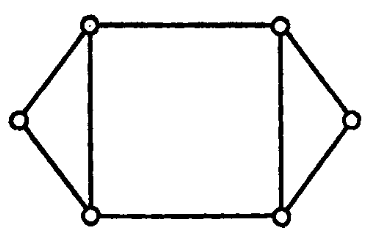
Рис. 4. Граф
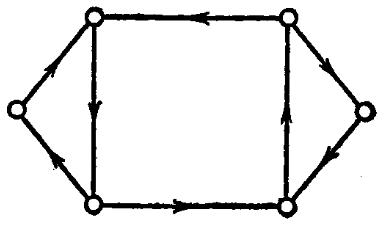
Рис. 5. сильно связный орграф
Теорема. Пусть G — связный граф; он ориентируем тогда и только тогда, когда каждое его ребро содержится по крайней мере в одном цикле.
Орграфы и матрицы
Матрицей смежностей А(D) орграфа D называется (р×р)-матрица ||aij||, у которой aij= 1, если ViVj- дуга орграфа D, и aij=0 в противном случае. Матрица смежностей которого имеет вид (рис. 6):
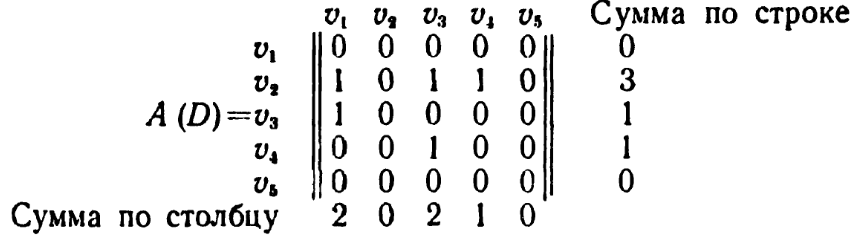
Рис. 6. Матрица смежности графа
Легко проверить, что суммы элементов по строкам матрицы A(D) равны полустепеням исхода вершин орграфа D, а суммы элементов по столбцам - полустепеням захода.
Как и в случае графов, степени матрицы смежностей А орграфа дают полную информацию о числе маршрутов, идущих из одной вершины в другую. Теорема. (i, j)-й элемент аijn матрицы А" равен числу маршрутов длины n, идущих из вершины vi в вершину vj.
Упомянем здесь вкратце еще о трех матрицах, связанных с орграфом Ds - о матрице достижимостей, матрице расстояний и матрице обходов. В матрице достижимостей R элемент rij равен 1,если вершина vi достижима из vj и равен 0 в противном случае. В матрице расстояний (i, j)-й элемент равен расстоянию из вершины vi в вершину vj; если же из vi в vj нет путей, то соответствующий элемент полагаем равным бесконечности. В матрице обходов (i, j)-й элемент равен длине наиболее длинного пути из vi в vj, а если таких путей нет, то опять-таки полагаем этот элемент равным бесконечности. Для орграфа D, показанного на рис. 7.
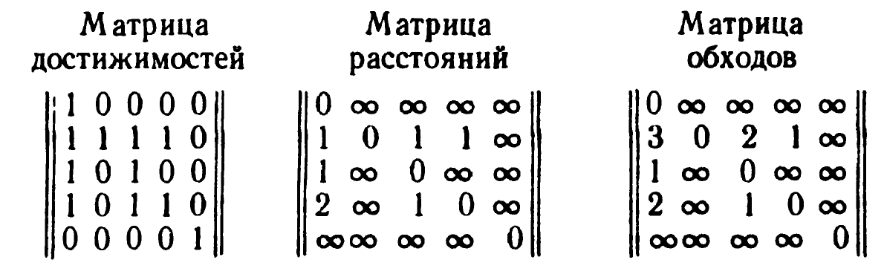
Рис. 7. Матрицы.
Следствие. Элементы матриц достижимостей и расстояний связаны со степенями матрицы А следующими соотношениями:
1) rii = 1 и dii = 0 для всех i;
2) rij = 1 тогда и только тогда, когда aijn> 0 для некоторого n;
3) d(vi,vj) равно наименьшему из чисел n, для которых aijn> 0
Эффективных методов для нахождения элементов матрицы обходов не существует. Эта проблема тесно связана с некоторыми другими давно поставленными алгоритмическими проблемами теории графов, такими, как нахождение остовных циклов и контуров, а также решение задачи о коммивояжере.
Поэлементное произведение В×С матриц B=||bij|| и C=||cij|| имеет своим (i, j)-м элементом bijcij. Матрицу достижимостей орграфа можно использовать для нахождения его сильных компонент.
Лекция 22. Сильносвязный орграф. Эйлеровы орграфы
Ориентированные эйлеровы графы
Ориентированной эйлеровой цепью ориентированного графа G называется замкнутая ориентированная цепь, содержащая все дуги G.
Открытой ориентированной эйлеровой цепью называется открытая ориентированная цепь, содержащая все дуги графа G.
Ориентированный граф, обладающий ориентированной эйлеровой цепью, называется ориентированным эйлеровым графом (рис. 1).
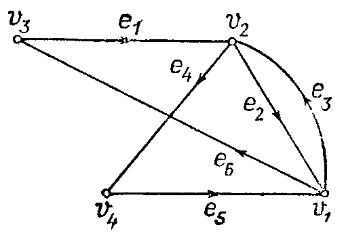
Рис. 1. Эйлеровы цепи.
Ориентированным эйлеровым графом является граф, изображенный на рис. 28, поскольку дуги е1 e2, е3, е4, е5, е6 образуют в графе G ориентированную эйлерову цепь.
Теорема. Для связного ориентированного графа G следующие утверждения равносильны:
1) G - ориентированный эйлеров граф;
2) для любой вершины v графа G справедливо равенство d - (v) = d+(v);
3) G - объединение нескольких реберно-непересекающихся контуров.
Рассмотрим, например, ориентированный эйлеров граф G на рис. 28. Легко проверить, что он обладает свойством, сформулированным в п. 2 теоремы, и является также объединением реберно-непересекающихся контуров {е2, е3) и {e1, e4, e5, e6}.
Легко доказать и следующую теорему:
Теорема. Связный ориентированный граф содержит открытую ориентированную эйлерову цепь тогда и только тогда, когда выполняются условия:
1) в графе G имеются такие две вершины v1 и v2, что d+ (v1)=d- (v1)+1 и d- (v2) = d+(v2)+1;
2) для любой вершины v, отличной от v1 и v2, справедливо равенство d- (v) - d+ (v).
Например, условиям этой теоремы удовлетворяет граф на рис. 2. Открытой ориентированной эйлеровой цепью графа G является последовательность e1, е2, e3, e4, е5, е6.
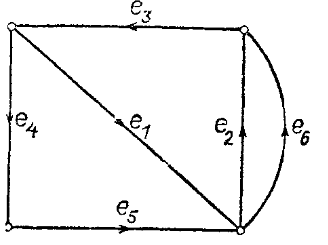
Рис. 2. Открытая ориентированная эйлеровая цепь.
Эйлеров контур в орграфе D — это замкнутый остовный маршрут, в котором каждая дуга орграфа D встречается по одному разу. Орграф называется эйлеровым, если в нем есть эйлеров контур.
Лекция 23. Базовые множества и принцип работы автоматов
Автомат– дискретный преобразователь информации, который на основе входных сигналов, поступающих в дискретные моменты времени, и с учетом своего состояния вырабатывает выходные сигналы и изменяет свое состояние.
В данном разделе рассматриваются абстрактные автоматы, т.е. некоторая математическая модель. Вопросы практической реализации не рассматриваются. В связи с этим при построении автоматов будем иметь в виду, что:
Автомат функционирует в абстрактном времени.
Все переходы происходят мгновенно.
Автомат представляет собой кортеж 6 –го порядка:
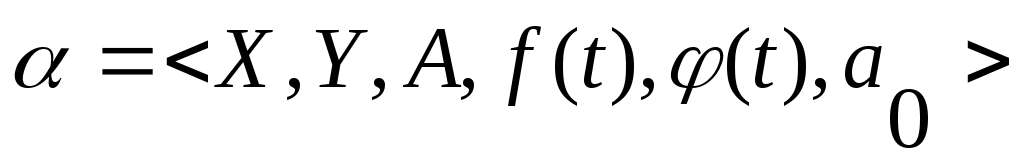 , ,
где 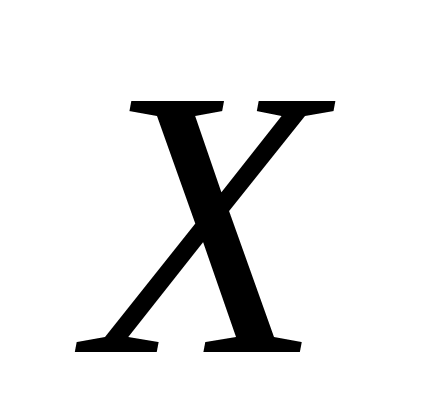 – множество входных сигналов (входной алфавит), – множество входных сигналов (входной алфавит),
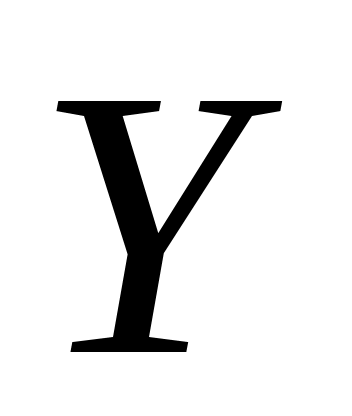 – множество выходных сигналов (выходной алфавит), – множество выходных сигналов (выходной алфавит),
 – множество внутренних состояний, – множество внутренних состояний,
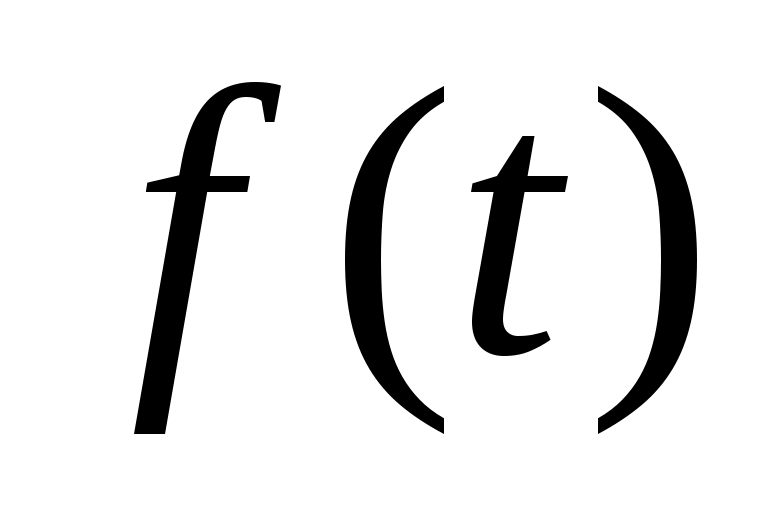 – функция перехода, – функция перехода,
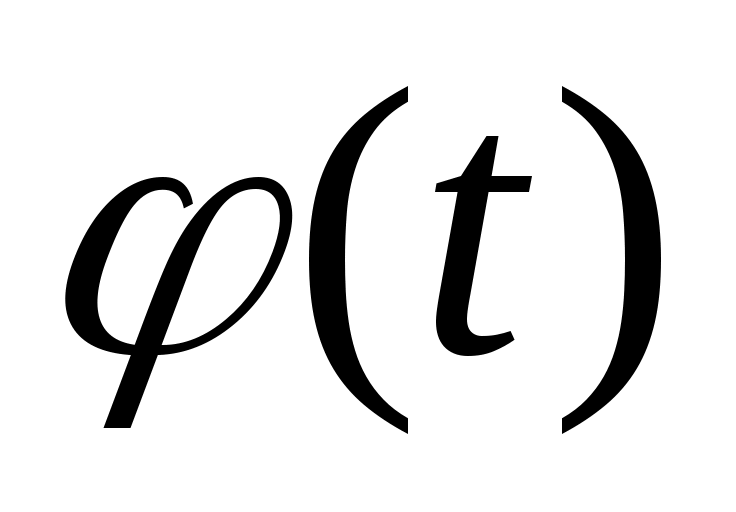 – функция выхода, – функция выхода,
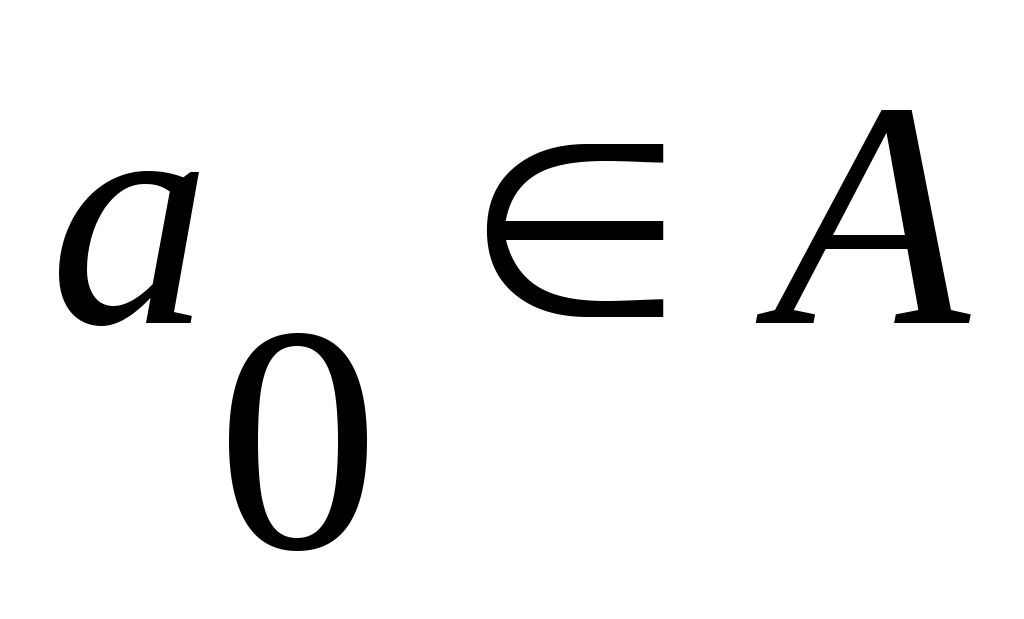 - начальное состояние автомата. - начальное состояние автомата.
Законы функционирования автоматов.
В зависимости от законов функционирования различают 3 вида автоматов:
Автоматы первого рода, или автоматы Мили:

Автоматы второго рода

Правильные автоматы второго рода, или автоматы Мура:
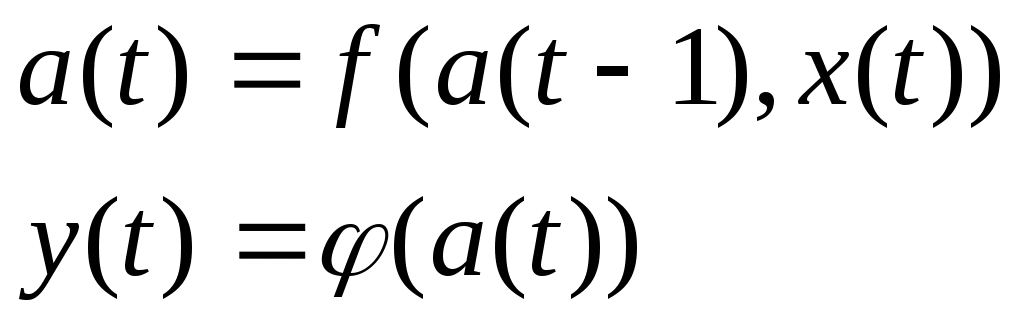
На практике наибольшее распространение получили автоматы Мили и автоматы Мура.
Задание автоматов
Автоматы могут быть заданы следующими способами:
В виде графа
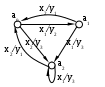
Рис. 1. Автомат Мили
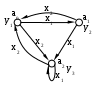
Рис.2. Автомат Мура.
При построении автомата Мили каждая дуга, соединяющая вершины  и и  , имеет обозначение , имеет обозначение 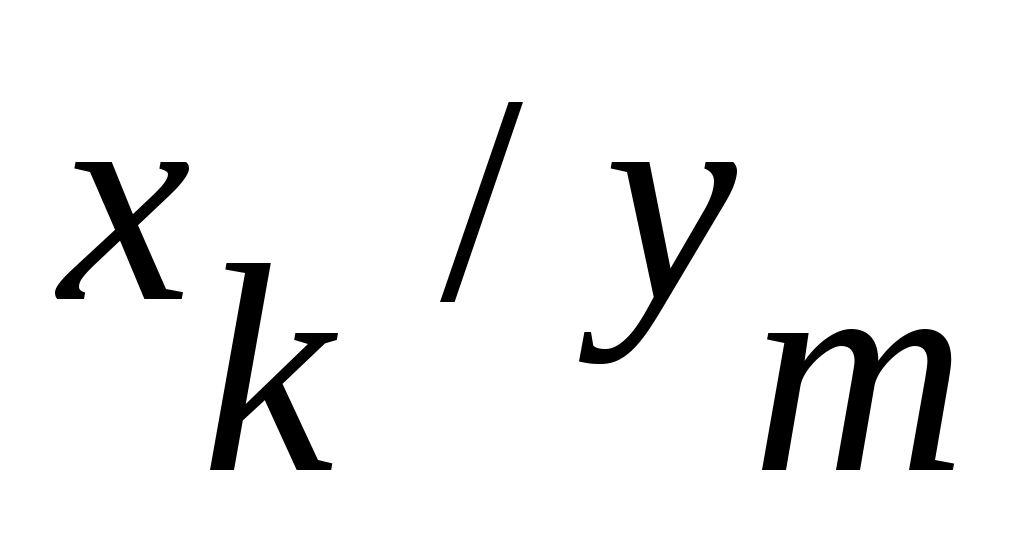 . Это означает следующее: находясь, в состоянии . Это означает следующее: находясь, в состоянии  автомат, отрабатывая входной сигнал автомат, отрабатывая входной сигнал 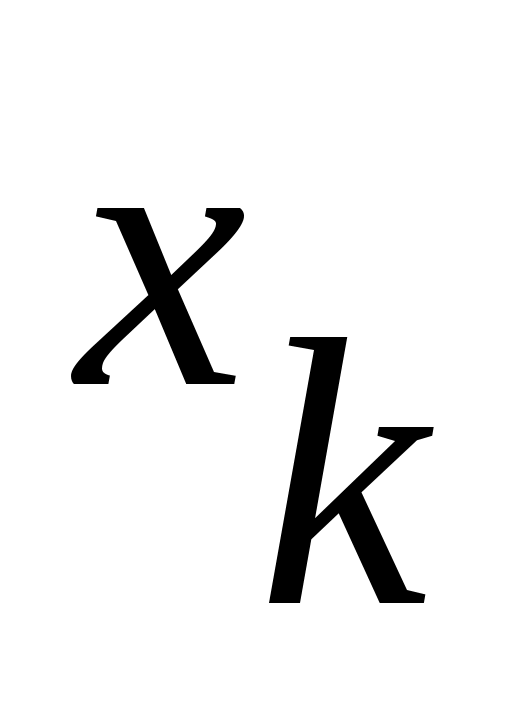 , выдает выходной сигнал , выдает выходной сигнал 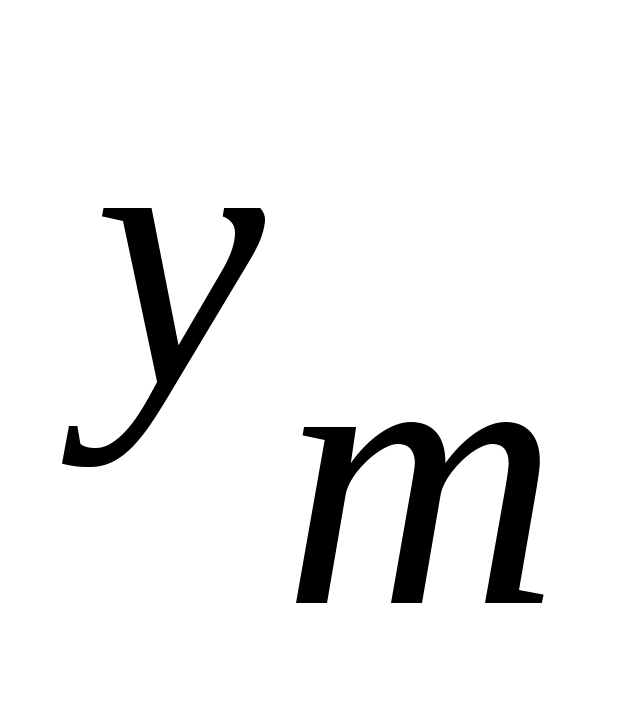 и переходит в состояние и переходит в состояние 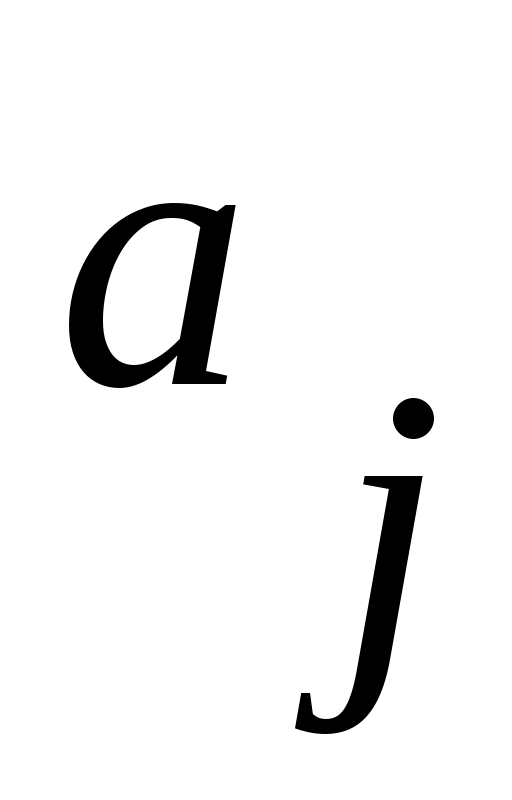 . .
Так как в автомате Мура выходной сигнал 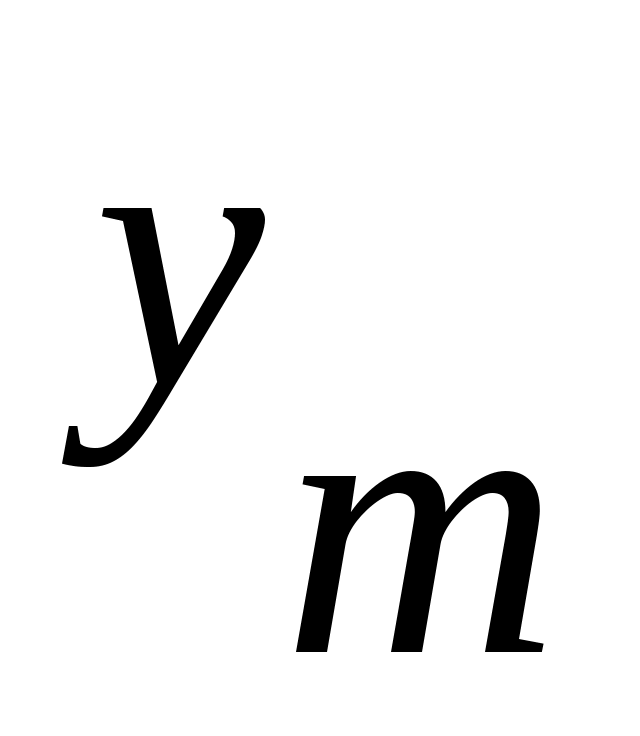 зависит только от текущего состояния зависит только от текущего состояния 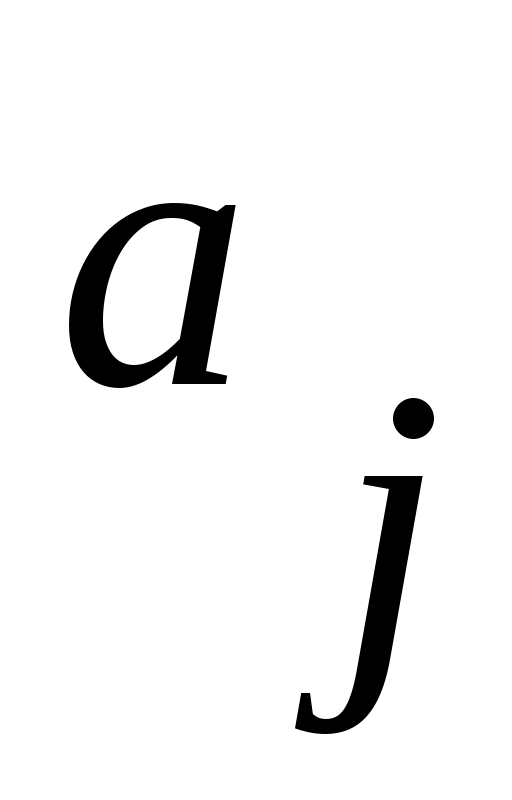 , то каждая дуга, соединяющая вершины , то каждая дуга, соединяющая вершины  и и 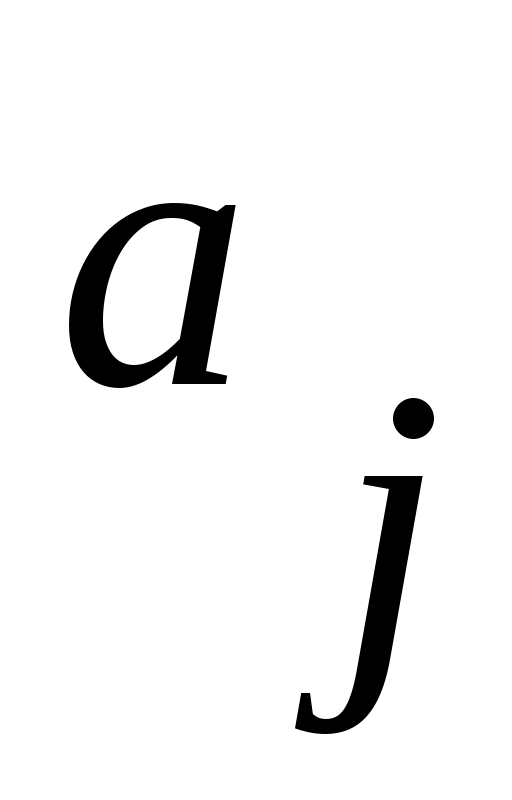 , имеет обозначение , имеет обозначение 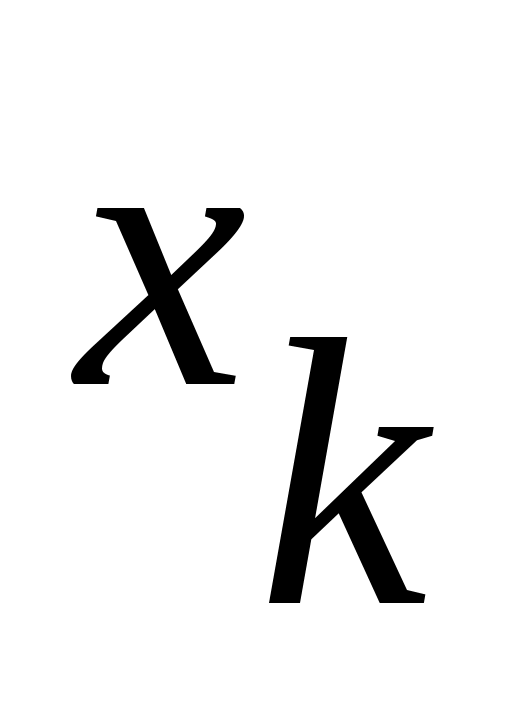 . .
В виде таблиц перехода и выхода (автомат Мили); отмеченной таблицы перехода (автомат Мура).
Автомат Мили описывается с помощью двух таблиц: таблицы перехода и таблицы выхода:
Таблица переходов (ТП) Таблица выходов (ТВ)
Автомат Мура описывается с помощью отмеченной таблицы перехода:
Таблица переходов (ТП)
-
Пример. Синтезировать автомат, на вход которого подаются монеты номинальной стоимостью 1, 2 и 3 копейки, а на выходе автомат выдает билет, если сумма набранных монет составляет 3 копейки, если сумма меньше 3 копеек, то автомат ничего не выдает, если сумма больше 3 копеек, то автомат возвращает деньги.
Определим входной, выходной алфавиты и множество внутренних состояний:
входной алфавит  - монеты номинальной стоимостью 1, 2 и 3 копейки - монеты номинальной стоимостью 1, 2 и 3 копейки
выходной алфавит 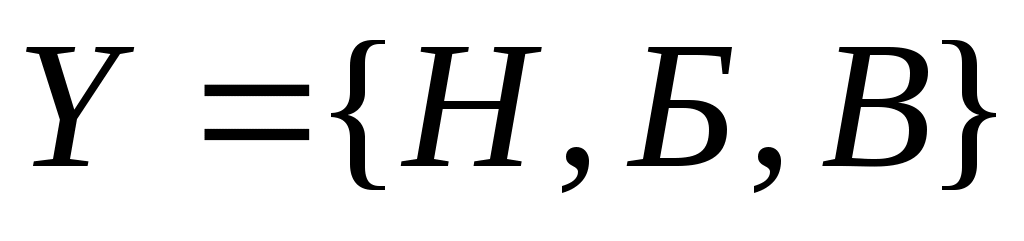 - на выходе возможны выходные символы: - на выходе возможны выходные символы:  - ничего; - ничего;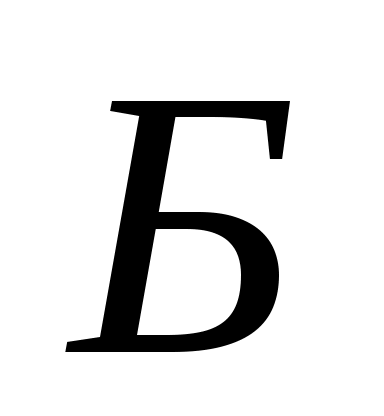 - билет; - билет;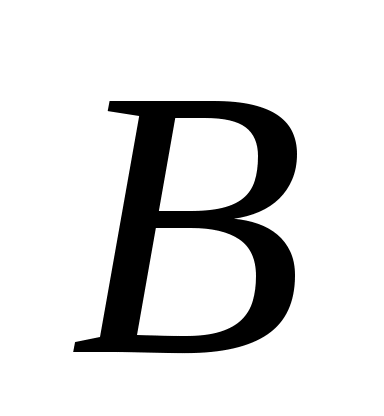 - возврат. - возврат.
множество внутренних состояний 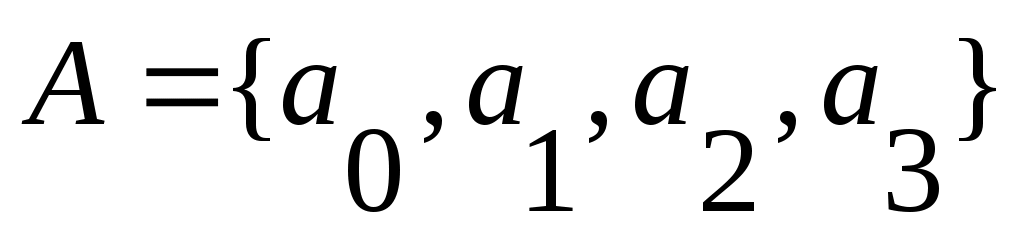 , ,
где 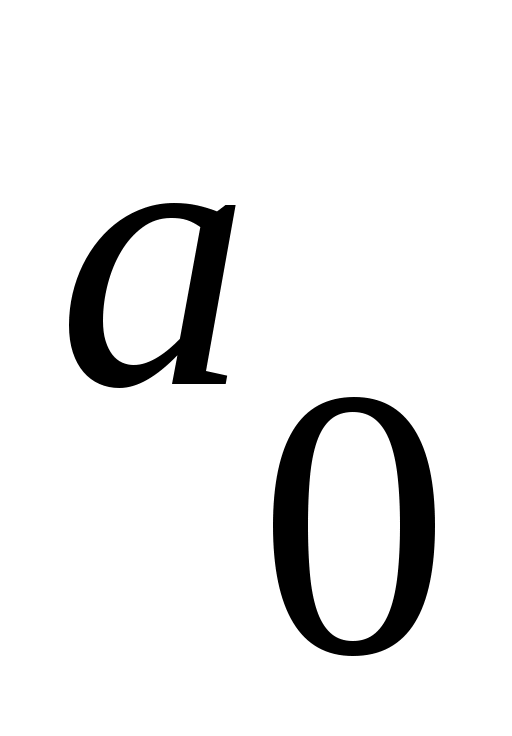 - начальное состояние автомата « в автомате ничего нет»; - начальное состояние автомата « в автомате ничего нет»;
 - «в автомате 1 копейка»; - «в автомате 1 копейка»;
 - «в автомате 1 копейка»; - «в автомате 1 копейка»;
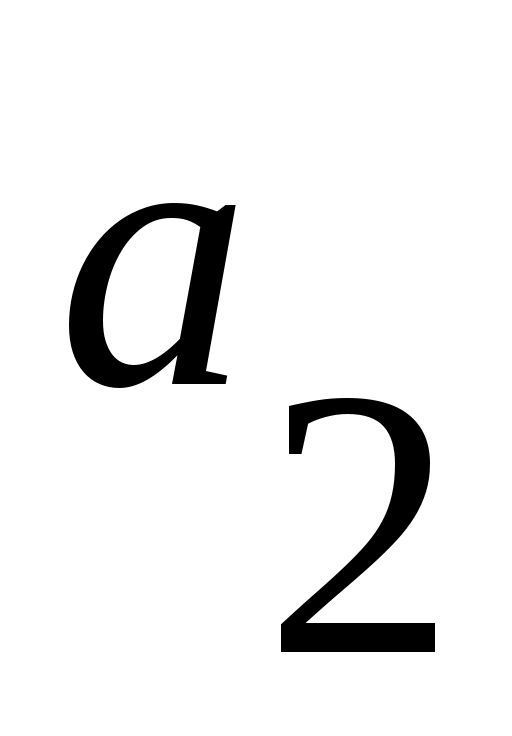 - «в автомате 2 копейки»; - «в автомате 2 копейки»;
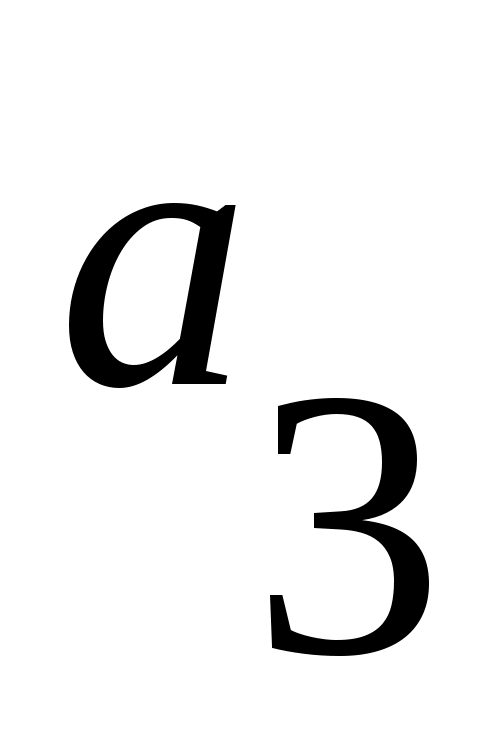 - «в автомате 3 копейки». - «в автомате 3 копейки».
Г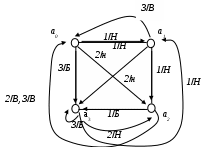 раф автомата имеет вид: раф автомата имеет вид:
Рис.3. Автомат Мили
Таблицы перехода и выхода представлены в виде:
Таблица переходов (ТП) Таблица выходов (ТВ)
|
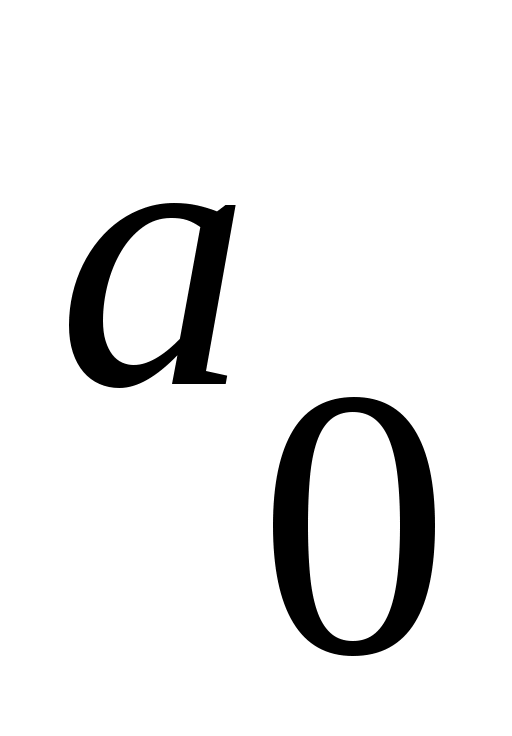
|

|
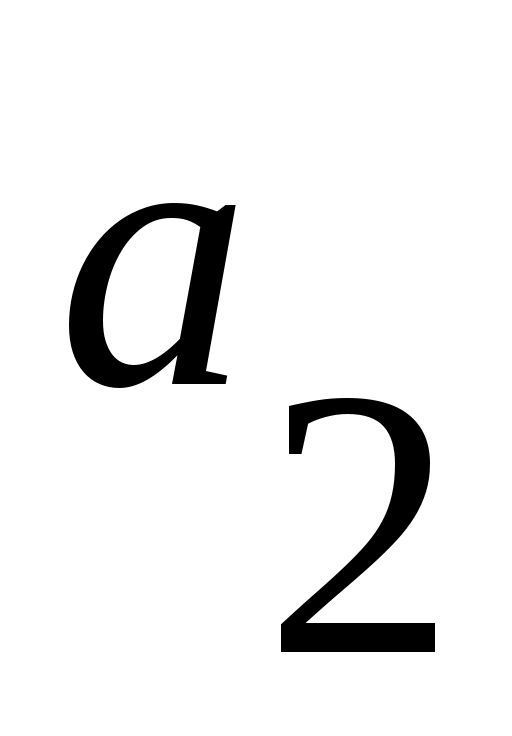
|
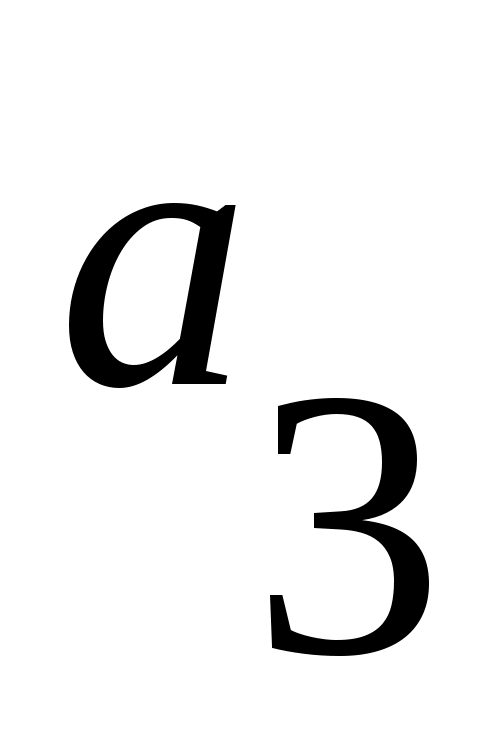
|
|
|
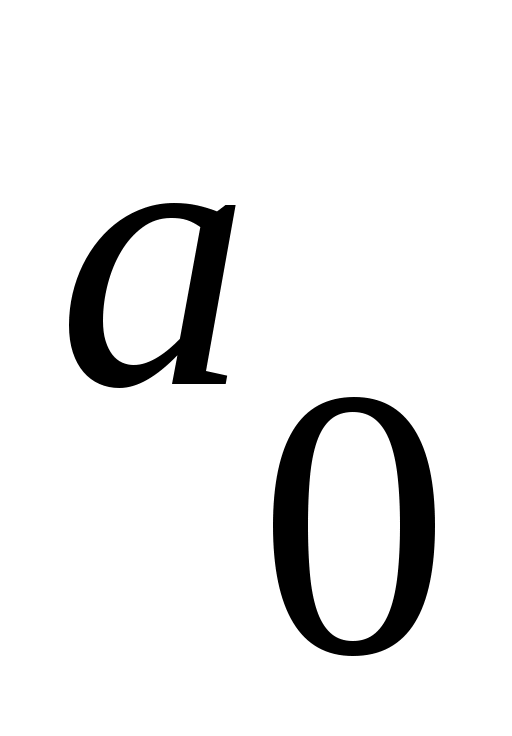
|

|
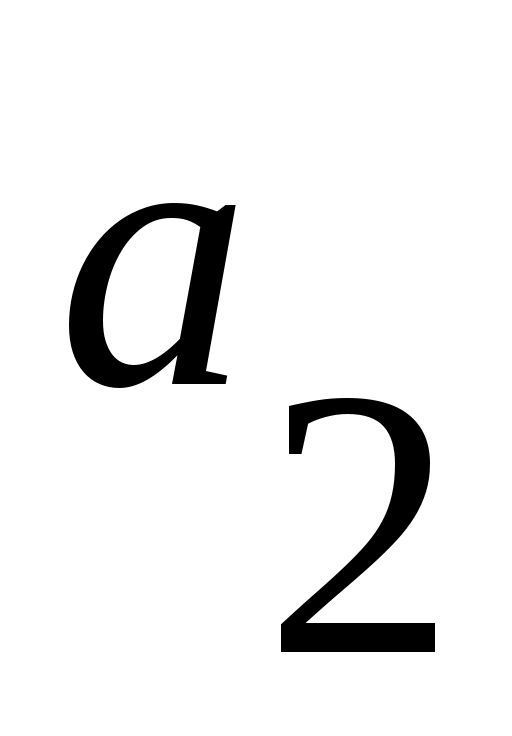
|
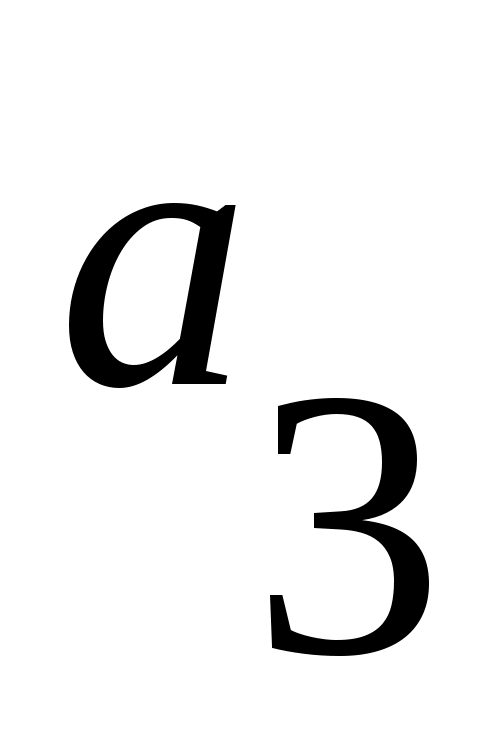
|
1
|

|
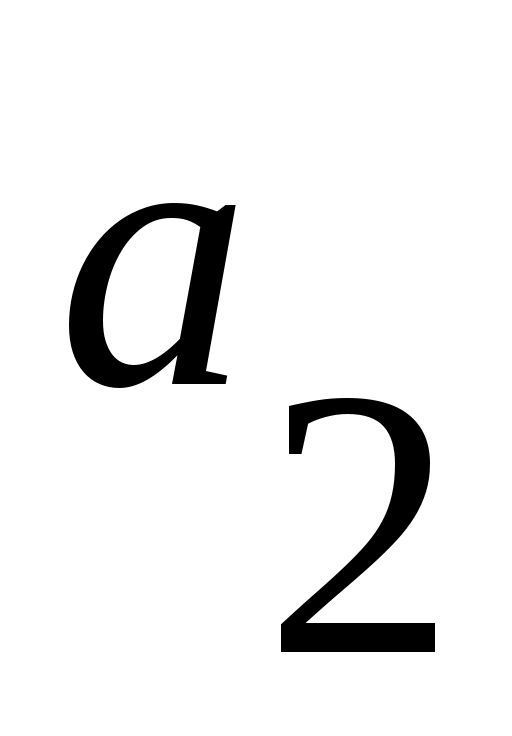
|
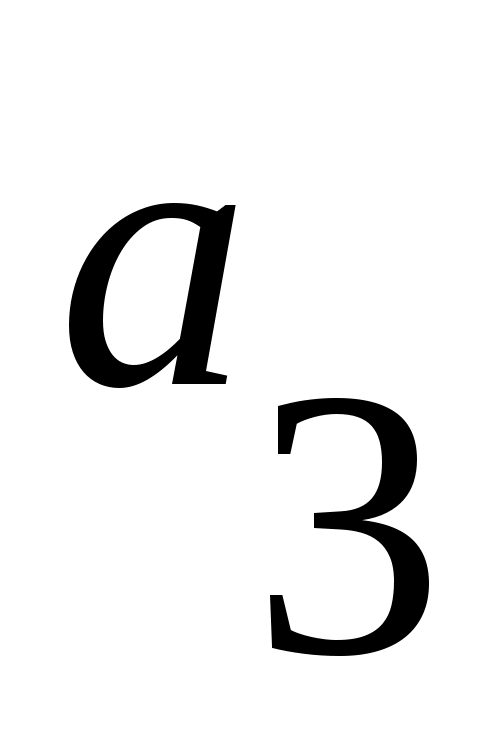
|

|
|
1
|
Н
|
Н
|
Б
|
Н
|
2
|
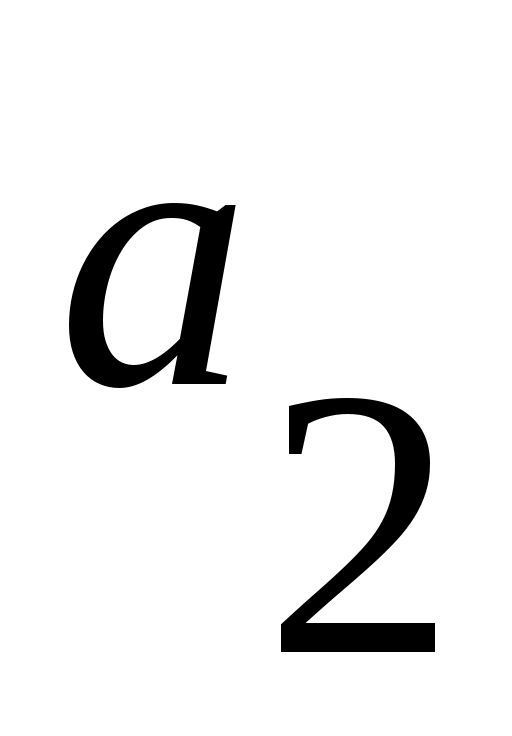
|
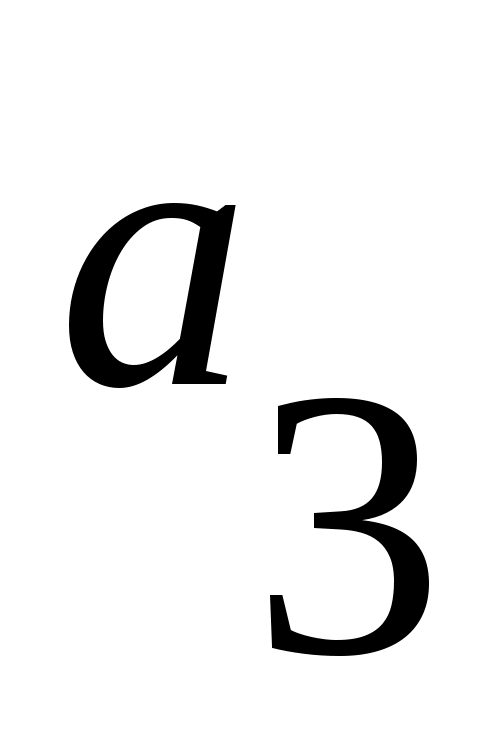
|
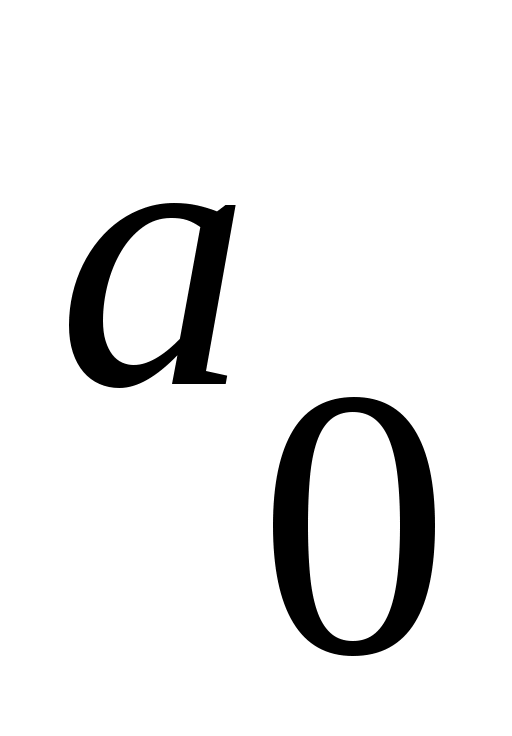
|
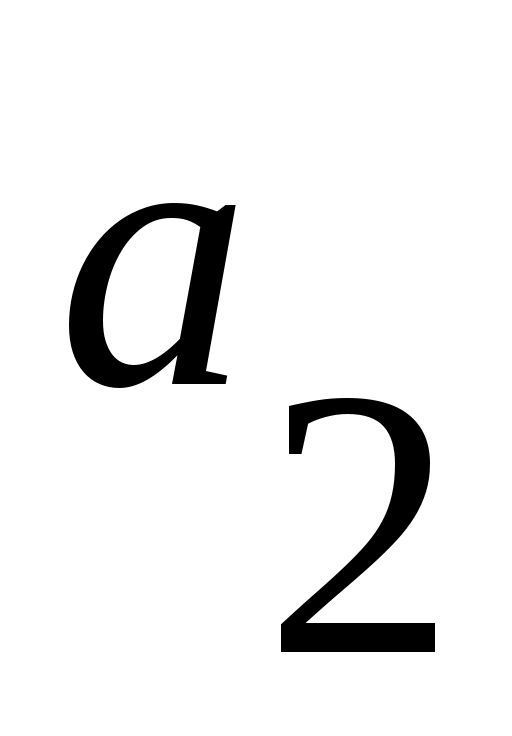
|
|
2
|
Н
|
Б
|
В
|
Н
|
3
|
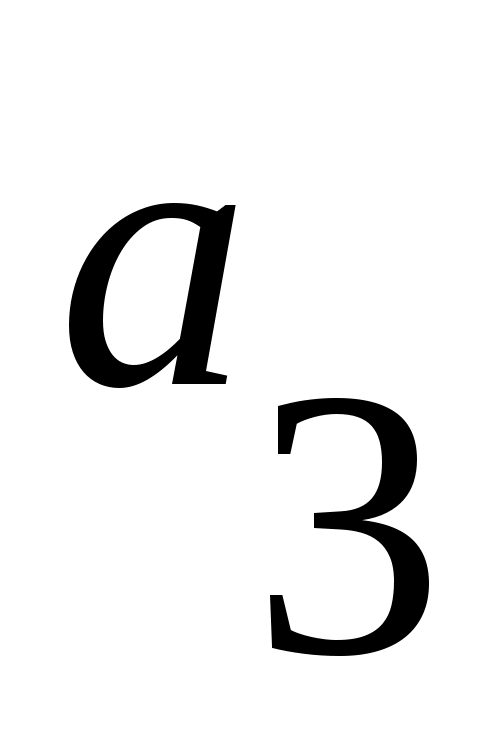
|
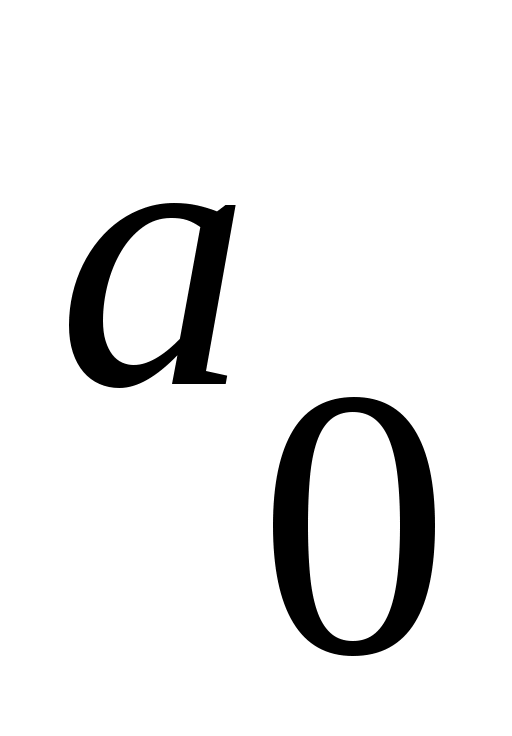
|
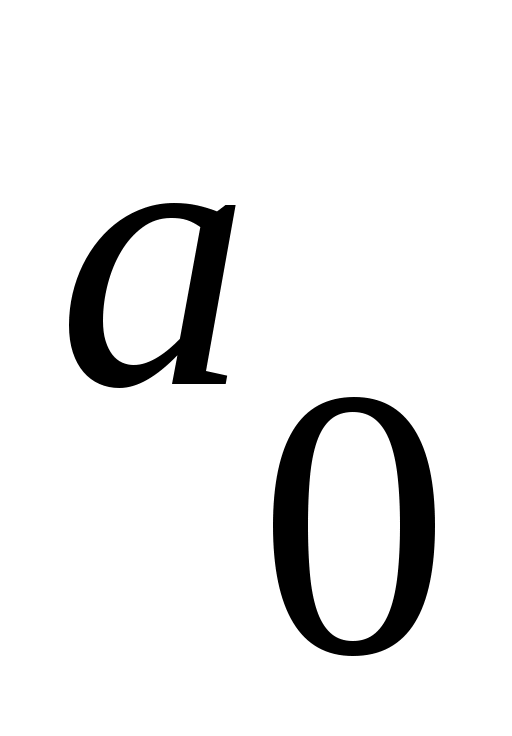
|
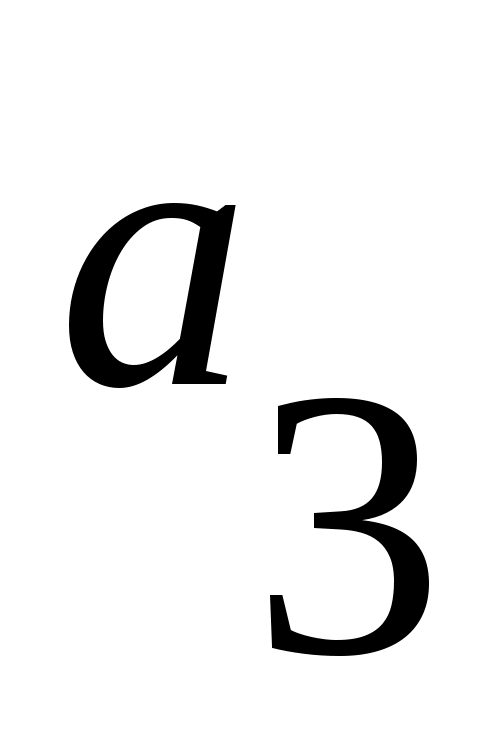
|
|
3
|
Б
|
В
|
В
|
Б
|
Неопределенным состоянием называется несуществующее состояние.
Частичным автоматомназывается автомат, в котором некоторые состояния в таблице перехода не определены. Для дальнейшего исследования неопределенное состояние некоторым образом доопределяют.
Минимизация автоматов
Входным словомназывается совокупность сигналов, поступающих на вход.
Выходным словомназываются совокупность сигналов на выходе.
Два автомата называются эквивалентными, если они имеют одинаковый входной и выходной алфавит, и на одинаковые входные слова выдают одинаковые выходные слова.
Два состояния одноэквивалентными , если на одинаковое входное слово выдается одинаковый выходной сигнал.
Два состояния k-эквивалентными, если на одинаковое входное слово длиной в k-единиц выдается одинаковый выходной сигнал длиной в k-единиц.
Эквивалентнымисостояниями называются k-эквивалентные состояния для любых k.
Эквивалентные состояния объединяются в класс эквивалентности.
Минимальный автомат – это автомат, состоящий из наименьшего числа состояний, каждое из которых является классом эквивалентности исходного автомата.
Алгоритм минимизации автомата Мили
По таблице выхода находятся состояния с одинаковыми выходными сигналами. Данные состояния объединяются в класс одноэквивалентных состояний. Проводится перекодировка.
По таблице перехода определяются классы двухэквивалентных состояний: для любого класса выделяется состояние, которое на одинаковый входной сигнал переходит в одинаковое состояние. Объединяем двухэквивалентные состояния в классы двухэквивалентных состояний. Проводится перекодировка.
Алгоритм выполняется, пока в классах k-эквивалентных состояний не находятся одинаковые состояния.
Вводятся новые состояния, соответствующие классам эквивалентных состояний.
С учетом новых состояний переписываются таблицы перехода и выхода.
|
 Скачать 2.15 Mb.
Скачать 2.15 Mb. раф автомата имеет вид:
раф автомата имеет вид: