Дискретная математика (1). Лекция Составные высказывания
 Скачать 2.15 Mb.
|
Сочетания с повторениями.Пример. На почте имеются открытки четырех видов: красные, желтые, зеленые и синие. Требуется 10 открыток. Сколькими способами можно их скомбинировать? Решение: Пусть мы отобрали 4 красных, 2 желтых, 2 зеленых и 2 синих открытки. Составим кортеж из 0 и 1. Выпишем столько единиц, сколько красная открытка встречается в нашем наборе, и поставим 0: 11110. Затем добавим кортеж для желтых -110. Получим 11110110. Добавим кортеж для зеленых и синих открыток. В последнем 0 не ставим. Получим кортеж 1111011011011. В нем 10 единиц и 3 нуля. Общая длина кортежа – 13. Таких кортежей можно составить столько, сколько перестановок с повторениями из 13.  (10,3)=  =286 – это и будет число сочетаний с повторениями из 4 по 10. (10,3)=  Таким образом, Ĉ .В общем случае. Пусть мы имеем n элементов  , , из которых создаются сочетания с повторениями, и каждое сочетание содержит k элементов. Составим кортеж, который запишем вначале столько единиц, сколько элемент входит в сочетание, затем запишем 0. припишем кортеж из единиц и нуль для элемента  и т.д. без последнего нуля. Получим: 111…1011…10…11…1Единиц – k. Нулей – n-1. Длина кортежа n+k-1 Общее число сочетаний с повторениями Ĉ  = (k,n-(k-1))=  = ,Итак, Ĉ = ,Лекция 18. Понятие графа. Способы задания графа. Методика выделения компонента связности в графе Графом G(V,E) называется совокупность двух множеств - непустого множества V (множества вершин) и множества Е неупорядоченных пар различных элементов множества V (Е - множество ребер). G(V,E):  , E VxV.Число вершин графа G обозначим р, а число ребер – q. р(G) = |V| q(G) = |E|. Часто рассматриваются следующие родственные графам объекты. 1. Если элементами множества Е являются упорядоченные пары, то граф называется ориентированным (или орграфом). В этом случае элементы множества V называются узлами, а элементы множества  - дугами (G(V, )).2. Если элементом множества Е может быть пара одинаковых (не различных) элементов V, то такой элемент множества Е называется петлей, а граф называется графом с петлями (или псевдографом). 3. Если Е является не множеством, а набором, содержащим несколько одинаковых элементов, то эти элементы называются кратными ребрами, а граф называется мультиграфом. Далее выражение: граф G(V,E) означает неориентированный граф без петель и кратных ребер. Обычно граф изображают диаграммой: вершины - точками (или кружками), ребра - линиями. Примеры. 1.  .  .Т.о. это неориентированный граф с петлей и кратными ребрами. 2 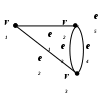 .  .  .Рис. 1. Неориентированный граф с петлей и кратными ребрами. Т.о. это ориентированный граф с петлей и кратными ребрами. 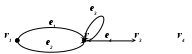 Рис. 2. Ориентированный граф с петлей и кратными ребрами. 3  .  .  , т.о.  Рис. 3. Неориентированный граф с петлей. |