мат мет-лекции-ИНТЕРНЕТ. Математические методы в психологии
 Скачать 2.19 Mb. Скачать 2.19 Mb.
|
Нормальное распределениеОдним из важнейших в математической статистике является понятие нормального распределения. Нормальное распределение (называемое также распределением Гаусса), характеризуется тем, что крайние значения признака в нем встречаются достаточно редко, а значения, близкие к средней величине – часто. Нормальное распределение возникает, когда данная случайная величина представляет собой сумму большого числа независимых случайных величин, каждая из которых играет в образовании всей суммы незначительную роль. Нормальное распределение имеет колоколообразную форму, значения моды, медианы и среднего арифметического равны между собой. Было установлено, что многие биологические параметры распределены подобным образом (рост, вес и так далее). Впоследствии психологи выяснили, что и большинство психологических свойств (показатели интеллекта, темпераментных особенностей, способностей и другие психические явления) также имеют нормальное распределение. Этот принцип учитывается при стандартизации тестовых методик. При этом, чем больше объем выборки, тем более полученное эмпирическое распределение приближается к нормальному. Характерное свойство нормального распределения состоит в том, что 68,26 % из всех его наблюдений всегда лежат в диапазоне 1 стандартное отклонение от среднего арифметического (какова бы ни была величина стандартного отклонения). 95,44 % - в пределах двух стандартных отклонений и 99,72 – в пределах трех стандартных отклонений. 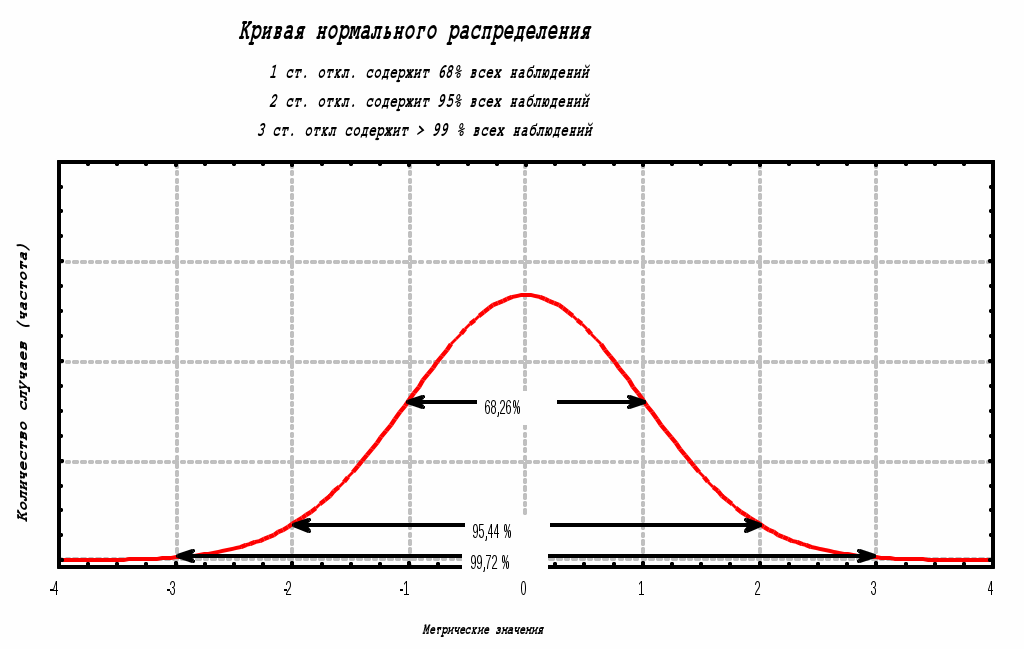 Асимметрия и эксцесс. Проверка нормальности распределения.Асимметрия – это показатель симметричности / скошенности кривой распределения, а эксцесс определяет ее островершинность. При левостронней асимметрии ее показатель является положительным и в распределении преобладают более низкие значения признака. При правостронней – показатель положительный и преобладают более высокие значения. У всех симметричных распеделений (в том числе и у нормального распределения) величина асимметрии равна нулю. Формула показателя асимметрии является следующей: Если в распределении преобладают значения близкие к среднему арифметическому, то формируется островершинное распределение. В этом случае показатель эксцесса стремится к положительной величине. У нормального распределения эксцесс равен нулю. Если у распределения 2 вершины (бимодальное распределение), то тогда эксцесс стремится к отрицательной величине. Показатель эксцесса определяется по формуле: Распределение оценивается как предположительно близкое к нормальному, если установлено, что от 50 до 80 % всех значений располагаются в пределах одного стандартного отклонения от среднего арифметического, и коэффициент эксцесса по абсолютной величине не превышает значения равного двум. Распределение считается достоверно нормальным если абсолютная величина показателей асимметрии и эксцесса меньше их ошибок репрезентативности в 3 и более раз. Постановка задачи: определить или опровергнуть факт нормальности распределения показателей субтеста «аналогии» из Таблицы данных Приложения (взято первые 20 случаев).
Для обработки данных понадобятся следующие последовательные шаги: вычисление Mx, , А, Е по уже известным формулам. Необходимо также определение ошибок репрезентативности асимметрии и эксцесса: В нашем случае: Как уже было сказано выше, принцип определения нормальности-ненормальности распределения является следующим: Поскольку оба показателя не превышают в 3 раза свою собственную ошибку репрезентативности, можно заключить, что распределение показателей субтеста «аналогии» соответствует нормальному. |
