Биометрия. Материалы для практического занятия. Предметом биометрии

• Название: Материалы для практического занятия. Предметом биометрии
• Анкор: Биометрия.docx
• Дата: 26.04.2017
• Размер: 1.29 Mb.
• Имя файла: Биометрия.docx
• Тип: Документы; #5939
• страница: 9 из 11

t-критерий Стьюдента (t-распределение).Использование формулы Гаусса—Лапласа (44) для сравнительной оценки средних величин затруднено тем, что в качестве аргументов в эту формулу входят генеральные параметры µ и σ (которые, как правило, остаются неизвестными), тогда как при обработке и сравнении выборочных групп приходится пользоваться не генеральными, а выборочными характеристикамииУчитывая это обстоятельство, английский математик В. Госсет (печатавшийся под псевдонимом Стьюдент), в 1908 г. Нашел закон распределения величины, в которой генеральный параметрзаменен на его выборочную характеристикут. е. нашел закон распределения значений



Оказалось, что отношение разности между выборочной и генеральной средними к ошибке выборочной средней непрерывно распределяется согласно следующей формуле:

для гдеС — константа, зависящая только от числа степеней свободы

Открытый Стьюдентом и теоретически обоснованный Р. Фишером закон t-распределения служит основой так называемой теории малой выборки, которая характеризует распределение выборочных средних в нормально распределяющейся совокупности в зависимости от объема выборки, t-распределение зависиттолько от числа степеней свободы k = n—1, причем с увеличением объема выборки пt-распределениебыстро приближается к нормальному с параметрами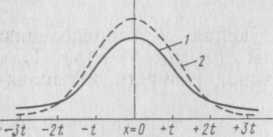ии уже при не отличается от него. Это видно из табл. 34, в которой наряду с табулированными значениями функции нормальногораспределения приведены табулированные значения t-распределения для разных значений t.



Рис. 20. Кривая t -распределения (1) при п—3 на фоне нормальной кривой (2)

Более наглядное представление о характере t-распределения дает рис. 20, на котором на фоне нормальной кривой изображена (более пологая) кривая t-распределения при п—3.t-распределение симметрично и отражает специфику распределения средней арифметической в случае малой выборки в зависимости от ее объема (п). Для выборок, объем которых превышает 30 единиц, величина / распределяется нормально и не зависит от числа наблюдений. Если жехарактер t-распределения находится в зависимости от числа наблюдений п.

Таблица 34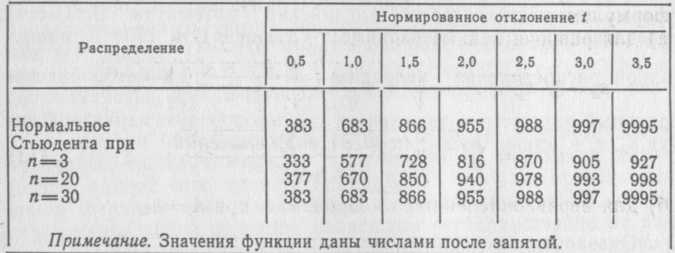



Для практического использования t-распределения составлена специальная таблица (см. табл. V Приложений), в которой содержатся критические точки(от англ.standard — норма, образец) для разных уровней значимостии чисел степеней свободы k. Как пользоваться этой таблицей в разных случаях применения /-критерия, будет показано ниже.

Оценка разности средних. Сравнивая друг с другом две независимые выборки, взятые из нормально распределяющихся совокупностей с параметрамииможно предположить, чтоа дисперсия этой разностиЗначения генеральных параметров неизвестны, однако несложно найти величины выборочных средних и разность между ними Нулевая гипотеза сводится к предположению, что Критерием для проверки-гипотезы служит отношение



где t— переменная величина, следующая t-распределению Стьюдента с числом степеней свободы k = (п₁ —1) + (п ₂—1) = = п₁ + п₂—2, а—ошибка указанной разности, обозначаемая в дальнейшем символом

Так как, согласно -гипотезе,то /-критерий выражается в виде отношения разности выборочных средних к своей ошибке, т. е.



-гипотезу отвергают, если фактически установленная величина t-критерия (обозначаемая символом) превзойдет или окажется равной критическому (стандартному) значению этой величины для принятого уровня значимостии числа степеней свободы k = п₁ + п₂—2, т. е. при условии

Ошибку разности среднихопределяют по следующим формулам:

а) для равночисленных выборок, т. е. при п₁ = п₂,





б) для неравночисленных выборок, т. е. при





В этой формуле вместоможно использовать

Пример 1. Изучали влияние кобальта на массу тела кроликов. Опыт проводили на двух группах животных: опытной и контрольной. Были исследованы кролики в возрасте от полутора до двух месяцев, массой тела 500—600 г. Опыт продолжался полтора месяца. Животных обеих групп содержали на одном и том же кормовом рационе. Однако опытные кролики в отличие от контрольных ежедневно получали добавку к рациону в виде водного раствора по 0,06 г хлористого кобальта на

1. 
   кг живой массы тела. За время опыта животные дали следующие прибавки живой массы тела (табл. 35).
   

Таблица 35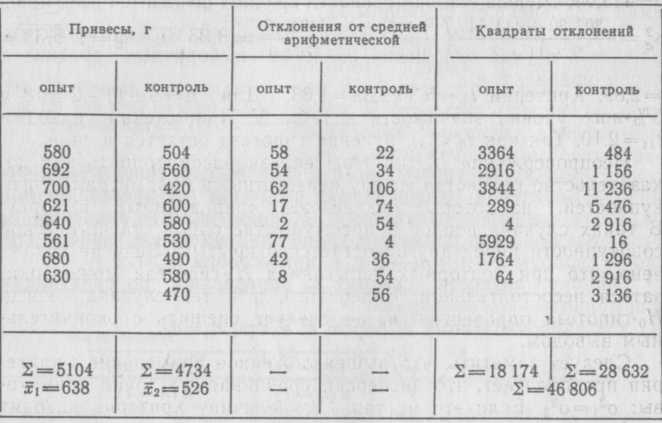



Средние арифметические привесов: в опыте =. в контроле Разница Чтобы установить, достоверна или случайна эта разница, нужно определить ошибку разности средних по формуле (74):



Отсюда По табл. V Приложений для 1%-ного уровня значимости и числа степеней свободы 6 = 9 + 8—2=15 находимТак какнулевая гипотеза опровергается на высоком уровне значимости (Р<0,01). Разница между средними величинами опыта и контроля оказалась в высшей степени достоверной.

Пример 2. На двух группах лабораторных мышей — опытнойи контрольной— изучали воздействие на организм нового препарата. После месячных испытаний масса тела животных, выраженная в граммах, варьировала следующим образом:



Разница между среднимиДля определения ошибки этой разности предварительно рассчитаем девиаты:

и Отсюда ошибка разности средних выразится величиной

иКритерий Для k=9+11—2=18 и 5%-ного уровня значимости в табл. V Приложений находим Так какнулевая гипотеза остается в силе.

НеопровержениеHо-гипотезы нельзя рассматривать как доказательство равенства между неизвестными параметрами совокупностей, из которых извлечены сравниваемые , выборки. В таких случаях вопрос о преимуществе одной статистической совокупности перед другой остается открытым. Ведь не исключено, что при повторных испытаниях H₀-гипотеза может оказаться несостоятельной. Более того, и в тех случаях, когда Hо-гипотеза опровергается, не следует спешить с окончательным выводом.

Следует заметить, что вышеизложенное применение t-критерия предполагает, что дисперсии сравниваемых групп одинаковы: Если это не так, то величину критерия находят по формуле



а число степеней свободы — по следующим формулам:

а) при

б) при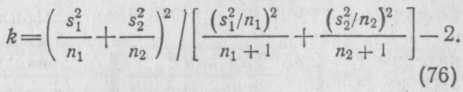

Так, при изучении влияния кобальта на массу тела кроликов (см. пример 1) дисперсии равныи(см. табл. 35). Видно, что

Следовательно, величину критерия необходимо определять с учетом неравенства дисперсий. Предварительно найдемиВеличина t-критерия равнаЗатем определяем .и В результате Дляив табл. V Приложений находим

Так както H₀-гипотеза отвергается.

Правильное применение t-критерия предполагает нормальное распределение совокупностей, из которых извлечены сравниваемые выборки, и равенство генеральных дисперсий. Если эти условия не выполняются, то t-критерий применять не следует. В таких случаях более эффективными будут непараметрические критерии.

Оценка средней разности между выборками с попарно связанными вариантами. Сравниваемые выборки нередко представляют собой ряды попарно связанных вариант, т. е. являются зависимыми выборками.В таких случаяхоценкой разности между генеральными средствамибудет средняя разность, определяемая из суммы разностей между попарно связанными вариантами сравниваемых групп, т. е.



Оценкой генеральной дисперсииразности среднихбудет выборочная дисперсия



В формулах (77) и (78) п — число парных наблюдений;величинаидентична разности средних, т. е.

Ошибку средней разностиобозначаемую символом определяют по формулам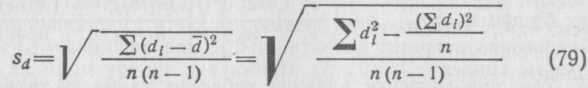



или

Если члены генеральной совокупности распределяются нормально, то и разности между нимибудут распределяться нормально и случайная