Биометрия. Материалы для практического занятия. Предметом биометрии

Название	Материалы для практического занятия. Предметом биометрии
Анкор	Биометрия.docx
Дата	26.04.2017
Размер	1.29 Mb.
Формат файла
Имя файла	Биометрия.docx
Тип	Документы #5939
страница	10 из 11

1 2 3 4 5 6 7 8 9 10 11

величина

будет иметь распределение Стьюдента с

степенями свободы. Hо-гипотеза сводится к предположению, что

Отсюда /-критерий выразится в виде отношения средней разности к своей ошибке, т. е.

Если

для принятого уровня значимости и числа степеней свободы k = n—1, то нулевая гипотеза должна быть отвергнута.

Пример 3. На протяжении ряда лет в условиях Одесской опытной станции изучали влияние черного и апрельского пара на урожай ржи. Результаты опыта учитывали по массе 1000 зерен (табл. 36).

Таблица Зв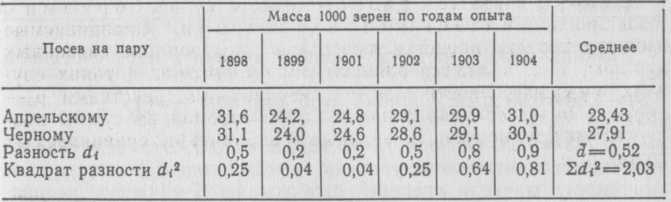

В табл. 36 приведены выборки с попарно связанными вариантами: несомненно, что каждый год имел свои специфические условия, которые одинаково влияли на урожай ржи, посеянной как по черному, так и по апрельскому пару. Поэтому обрабатывать полученные данные нужно с учетом тех условий, в которых проводили эксперимент. Из табл. 36 видно, что урожай ржи по апрельскому пару несколько выше, чем по черному. Средняя разность

Определяем ошибку этой разности:

Критерий

Для

(см. табл. V Приложений). Так как

то Н₀-гипотезу отвергают на высоком уровне значимости

Следовательно, с вероятностью

можно утверждать, что

разница между сравниваемыми выборками статистически достоверна.

Пример 4. В результате семилетних исследований урожайности ячменя и овса в условиях нечерноземной зоны РСФСР были получены следующие данные (табл. 37).

Таблица 37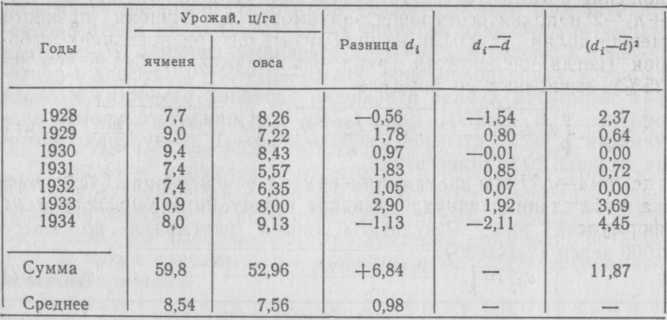

Разница между средним урожаем ячменя и овса составила 8,54—7,56 = 0,98 ц/га. Ошибка этой разницы

Отсюда

Эта величина не превышает критический уровень

для 5%-ного уровня

значимости и числа степеней свободы k= (7—1)=6. Следовательно, нулевую гипотезу здесь отбросить нельзя.

Оценку средней разности можно произвести по доверительномуинтервалу, построенному на основании полученной разностии ее ошибкиЕсли нижняя граница доверительного интервала окажется с положительным знаком, это будет свидетельствовать о достоверности разницы. Если же нижняя граница доверительного интервала будет с отрицательным знаком, это будет служить указанием на случайный характер наблюдаемой средней разности.

Так, в примере

Нижняя

граница 95%-ного доверительного интервала (0,52—0,24 = 0,28) оказалась с положительным знаком, тогда как в примере 4

и нижняя граница доверительного интервала (0,98—1,04= —0,06) оказалась с отрицательным знаком, что не дает основания для отклонения нулевой гипотезы.

Оценка разности между долями. Выборочная доля зависит от числа единиц в выборке, имеющих учитываемый признак, а общее число таких единиц в генеральной совокупности определяет генеральнуюдолюОценкой разности между генеральными долями

служит разность между выборочными долями

Отношение этой разностик своей ошибке дает случайную величину

котораяследует t-распределению Стьюдента. H₀-гипотезу, или предположение о том, что

отвергают, если

для k = п₁ + п₂—2 и принятого уровня значимостиОшибка разности между долями, взятыми из приблизительно равновеликих выборок (когда численности групп различаются не более чем на 25%), вычисляют по формуле

где

Если доли выражены в процентах от общего числа наблюдений, ошибку разности между ними определяют по формуле

Сопоставляемые группы п₁и п₂могут быть выражены абсолютными числами т₁и m₂. Ошибка наблюдаемой между ними разности определяется по следующей формуле:

но так как

то формулу (81) можно представить и в таком виде:

Когда сравнивают доли из неравновеликих выборок и при

ошибку разности между ними определяют по формуле

р определяют как средневзвешенную из и долей, или же из абсолютных численностей групп:

В этих формулах n₁ и n₂ — численности групп, на которых определяют доли

Если доли выражают в процентах от п, то вместо

нужно брать

Если же неравновеликие группы выражены абсолютными числамииошибку разности между ними определяют по формуле

Тема № 7.Регрессионный анализ.

Цель– познакомиться с регрессионным анализом.

Краткое содержание.

График корреляционной зависимости по уравнению функции ỹ_x=f(x) или ẍ_y,=f(у). Условные средние. Регрессия как изменение функции в зависимости от изменений одного или нескольких аргументов. Уравнения регрессии, эмпирические и теоретически вычисленные ряды регрессии, их графики, линии регрессии, коэффициенты линейной и нелинейной регрессии. Задача регрессионного анализа - предвидеть возможные изменения одного признака Y на основании известных изменений другого X, связанного с первым корреляционно. Основная характеристика коэффициента регрессии. Расчет коэффициентов регрессии, составление уравнений регрессии. Работа в среде Ехсеl. Расчет коэффициентов регрессии, составление уравнений регрессии с помощью средств электронных таблиц и функций Ехсеl, а также при использовании пакета «Анализ данных».

Тема № 8.Дисперсионный анализ.

Цель– познакомиться с дисперсионным анализом.

Краткое содержание. Результативные признаки. Факторы как причины изменения величины результативного признака. Регулируемые или организованные факторы и нерегулируемые. Градации регулируемого фактора. Дисперсионный анализ - разложение общей изменчивости признака на составные части: вариацию, определяемую действием изучаемого конкретного фактора, и вариацию, вызываемую случайными факторами. Дисперсионный однофакторный комплекс - действие на признак одного регулируемого фактора. Дисперсионные комплексы равномерные, пропорциональные (ортогональные) и неравномерные (неортогональные). Группировка совокупности по признаку-фактору. Выявление степени влияния признака-фактора на признак-результат по расчету нескольких видов дисперсий: общей, межгрупповой и внутригрупповой. Правило сложения дисперсий. Отношение межгрупповой дисперсии (факториальной дисперсии) к внутригрупповой, или остаточной, дисперсии - критерий оценки влияния, регулируемых в опыте факторов на результативный признак. Двух-, трех-и многофакторный анализ - действие на признак двух, трех или большего числа регулируемых факторов. Общие схемы дисперсионного анализа двухфакторных ортогональных комплексов. Анализ двухфакторных комплексов - действие каждого фактора в отдельности и их совместное действие на результативный признак. Неортогональные комплексы. Работа в среде Ехсеl. Анализ однофакторных и двухфакторных комплексов - действие каждого фактора в отдельности и их совместное действие на результативный признак с помощью средств электронных таблиц и функций Ехсеl, а также при использовании пакета «Анализ данных». Расчет силы влияния факторов.

Тема № 9.Вопросы планирования исследования

Цель– изучить вопросы планирования исследования.

Задачи. Приближенные оценки основных статистических показателей. Определение необходимого объема выборки.

Краткое содержание. Классические работы Р. Фишера открыли новую страницу в истории биометрии: они показали, что планирование экспериментов и обработка их результатов — это две тесно связанные между собой задачи статистического анализа. Это открытие легло в основу разработки теории планирования экспериментов, которая в настоящее время находит применение не только при проведении сельскохозяйственных опытов, на базе которых она возникла, но и в различных областях биологии, медицины, антропологии, в сфере других научно-практических дисциплин, включая и социально-экономические исследования.

Планирование экспериментов, как уже отмечалось в предисловии к этой книге, стало самостоятельным разделом биометрии, которому посвящена огромная литература. В начальном курсе биометрии невозможно осветить все аспекты теории экспериментов. Здесь будут рассмотрены лишь некоторые общие положения, относящиеся к этой сложной и многогранной проблеме.

Термин «эксперимент» (от лат. experimentum — опыт) означает искусственно организуемый комплекс условий, в которых испытывают воздействие того или иного фактора или одновременно нескольких факторов на результативный признак. В земледелии это полевые опыты; в животноводстве — опыты по кормлению животных, по уходу за ними; в педагогике — опыты по проверке новых методов обучения и воспитания учащихся; в фармакологии — испытание эффективности новых лечебных препаратов; в медицине— проверка разных способов лечения больных и т. д.

Исследовательская работа не только сводится к экспериментам; ее проводят и вне их на основе непосредственных наблюдений. Так что выражение «планирование исследований» оказывается более емким, а следовательно, и более подходящим, чем введенный Р. Фишером (1930) термин «планирование экспериментов». Конечно, и термин «эксперимент» можно применять в более широком смысле, понимая под ним любые испытания, проводимые исследователем в отношении изучаемого объекта. При всем разнообразии методов исследовательской работы задача планирования сводится к тому, чтобы при возможно минимальных объемах наблюдений получать достаточно полную информацию об изучаемых объектах.

С варьированием результатов наблюдений связана повторность вариантов опыта, позволяющая повысить точность оценок генеральных параметров, надежность выводов, которые делает исследователь на основании выборочных.показателей. Под повторностью в полевом опыте понимают число одноименных делянок для каждого варианта опыта. В лабораторных условиях повторность может выражаться числом одинаковых проб серий одновременных испытаний, измерений и т. п. повторений одного и того же варианта опыта. Очевидно, чем шире диапазон варьирования признака, тем больше должна быть и повторность опыта, и, наоборот, при слабом варьировании учитываемого признака число вариантов опыта, т. е. их повторность, уменьшается. В такой же зависимости от размаха варьирования признаков находится и организация планирования минимально допустимого числа испытаний.

Приближенные оценки основных статистических показателей.

Прежде чем наметить необходимый объем выборки, надо определить среднюю величину и ее ошибку для варьирующего признака— характеристики, которые позволяют использовать показатель точности выборочной средней при решении этой задачи. Приближенное значение средней арифметической х можно определить по полусумме лимитов:

$d:\тгу\дисциплины\1семестр\биометрия\media\image1.jpeg$

а среднее квадратическое отклонение— по разности лимитов, отнесенной к коэффициентуК, который устанавливают в зависимости от объема выборки (п) с помощью табл. 136 (по Н. А. Плохинскому, 1970), т. е. по формуле

$d:\тгу\дисциплины\1семестр\биометрия\media\image5.jpeg$

Пример 1. Зная лимиты $d:\тгу\дисциплины\1семестр\биометрия\media\image6.jpeg$ и $d:\тгу\дисциплины\1семестр\биометрия\media\image7.jpeg$

кальция в сыворотке крови обследованной группы обезьян (я= = 100), можно определить основные характеристики для этой выборки:

$d:\тгу\дисциплины\1семестр\биометрия\media\image8.jpeg$ и $d:\тгу\дисциплины\1семестр\биометрия\media\image9.jpeg$

Эти величины близки к фактически найденным: $d:\тгу\дисциплины\1семестр\биометрия\media\image11.jpeg$ и $d:\тгу\дисциплины\1семестр\биометрия\media\image10.jpeg$

Таблица 136

$d:\тгу\дисциплины\1семестр\биометрия\media\image3.jpeg$

Величину ошибки среднейможно определить по следующей приближенной формуле:

$d:\тгу\дисциплины\1семестр\биометрия\media\image4.jpeg$

Так, в данном случае $d:\тгу\дисциплины\1семестр\биометрия\media\image13.jpeg$ . Эта же величина получается и при использовании основной формулы $d:\тгу\дисциплины\1семестр\биометрия\media\image14.jpeg$ $d:\тгу\дисциплины\1семестр\биометрия\media\image15.jpeg$ . Отсюда показатель точностивыборочной

средней $d:\тгу\дисциплины\1семестр\биометрия\media\image18.jpeg$ Это очень высокая точность. Намечаемый таким образом объем выборки можно считать вполне достаточным для получения надежных оценок генеральных параметров (при условии , что совокупность, из которой взята выборка, распределяется по нормальному закону).

Определение необходимого объема выборки.

Элементарная логика и практический опыт подсказывают, что неразумно стремиться к неоправданно большому числу испытаний, если убедительный результат можно получить при минимально допустимом объеме выборки. Необходимая численность выборки

1 2 3 4 5 6 7 8 9 10 11