Биометрия. Материалы для практического занятия. Предметом биометрии

• Название: Материалы для практического занятия. Предметом биометрии
• Анкор: Биометрия.docx
• Дата: 26.04.2017
• Размер: 1.29 Mb.
• Имя файла: Биометрия.docx
• Тип: Документы; #5939
• страница: 7 из 11

Требования, предъявляемые к точечным оценкам. Выборочные характеристики как величины случайные, варьирующие вокруг своих генеральных параметров, в основном не совпадают с ними по абсолютной величине. Оценки должны удовлетворять по меньшей мере следующим требованиям: быть состоятельными, эффективными и несмещенными.

Для пояснения смысла этих свойств необходимо рассмотреть понятие выборочного распределения некоторой статистики. Пусть из бесконечно большой генеральной совокупности случайным образом извлекается большое число выборок, каждая из которых включает одно и то же количество наблюдений п. В каждой из этих выборок вычисляют значение статистики и. В силу случайных причин эти величины будут варьировать, образуя некоторое распределение, которое называют выборочным распределением статистики.

В тех случаях, когда распределение анализируемого признака не слишком сильно отличается от нормального вида, а объем выборок не слишком мал, очень часто выборочные распределения многих статистик оказываются нормальными. Поэтому их свойства можно описать только двумя параметрами: математическим ожиданием статистики µ_ии ее дисперсией σ_и².

Точечная оценка статистики называется состоятельной, если при увеличении объема выборки она стремится к величине генерального параметра. Так, для генеральной средней µ состоятельной оценкой является выборочная средняя х_ср, для генеральной дисперсии σ_х² состоятельной оценкой будет выборочная дисперсия Sx². Точечная оценка называется эффективной, если она имеет наименьшую дисперсию выборочного распределения по сравнению с другими аналогичными оценками, т. е. обнаруживает наименьшую случайную вариацию. Так, из трех показателей, описывающих положение центра нормального распределения некоторого признака X (средней арифметической, медианы и моды), наиболее эффективной оказывается первая х_ср, наименее эффективной —последняя Мо, так как для дисперсий этих оценок характерно σ²_хср< σ ²ме< σ ²м₀. Оценка называется несмещенной, если математическое ожидание ее бесконечного распределения совпадает со значением генерального параметра.

Выборочная средняя является несмещенной оценкой генеральной средней, тогда как выборочная дисперсия представляет собой смещенную оценку относительно генерального параметра на величину п/(п—1). Чтобы получить несмещенную оценку генеральной дисперсии, нужно при вычислении выборочной дисперсии, а следовательно, и среднего квадратического отклонения сумму квадратов отклонений (девиату) относить не к числу наблюдений п, а к числу степеней свободы (k=n—1).

Статистические ошибки. Выборочные характеристики, как правило, не совпадают по абсолютной величине с соответствующими генеральными параметрами. Величину отклонения выборочного показателя от его генерального параметра называют статистической ошибкой или ошибкой репрезентативности. Статистические ошибки присущи только выборочным характеристикам, они возникают в процессе отбора вариант из генеральной совокупности.

Для измерения ошибки репрезентативности некоторой статистики может служить дисперсия выборочного распределения σ_и² или найденное на ее основе значение среднего квадратического отклонения, которое называют также квадратической ошибкой статистики σ_и. Его величина показывает, насколько велика случайная вариация отдельных оценок по отношению к центру выборочного распределения, совпадающего со значением генерального параметра, если статистика несмещенная.

Из теории математической статистики известно, что в том случае, когда распределение исходного признака X не слишком сильно отличается от нормального вида, а объем выборки не слишком мал (на практике п≥30), квадратическая ошибка репрезентативности средней арифметической может быть найдена по формуле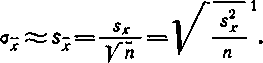

52

Sx=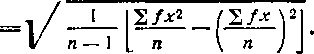

Ошибку средней арифметической обозначают также буквой т.

Приведенные формулы применяют при вычислении ошибки средней арифметической способом произведений. Они показывают, что при простой случайной выборке величина ошибки зависит как от объема выборки, так и от размаха варьирования признака в генеральной совокупности.

Тема № 4.КОРРЕЛЯЦИОННЫЙ АНАЛИЗ

Цель– научиться применять корреляционный анализ

Задачи. Функциональная зависимость и корреляция.Коэффициент корреляции.Ковариация.Вычисление коэффициента корреляции. Малые выборки.Множественная корреляция.Частная корреляция. Ошибка коэффициента корреляции.

Краткое содержание.

Функциональная зависимость и корреляция. Еще Гиппократ в VI в. до н. э. обратил внимание на наличие связи между телосложением и темпераментом людей, между строением тела и предрасположенностью к тем или иным заболеваниям. Определенные виды подобной связи выявлены также в животном и растительном мире. Так, существует зависимость между телосложением и продуктивностью у сельскохозяйственных животных; известна связь между качеством семян и урожайностью культурных растений и т. д. Наличие связей между варьирующими признаками обнаруживается на всех уровнях организации живого. Поэтому естественно стремление использовать эту закономерность в интересах человека, придать ей более или менее точное количественное выражение.

Для описания связей между переменными величинами применяют математическое понятие функции f, которая ставит в соответствие каждому определенному значению независимой переменной X, называемой аргументом, определенное значение зависимой переменной У: y = f(x). Здесь х—аргумент, а y соответствующее ему значение функции f(x). Такого рода однозначные зависимости между переменными величинами У и X называют функциональными. Примеров функциональной зависимости между переменными величинами много. Известно, что повышение температуры на 10 °С ускоряет химическую реакцию в два раза, объем куба однозначно определяется по длине одного из его ребер и т. д.

Однако такого рода однозначные, или функциональные, связи между переменными величинами встречаются далеко не всегда. Известно, например, что между ростом и массой тела у человека существует положительная связь: более высокие индивиды имеют обычно и большую массу тела, чем индивиды низкого роста. То же наблюдается и в отношении качественных признаков: блондины, как правило, имеют голубые глаза, а брюнета — карие. Однако из этого правила существуют исключения, когда сравнительно низкорослые индивиды оказываются тяжелее высокорослых, и среди населения, хотя и не часто, встречаются кареглазые блондины и голубоглазые брюнеты.

Причиной таких «исключений» является тот факт, что каждый биологический признак представляет собой функцию многих переменных: на него влияют и генетические, и средовые факторы, что и обусловливает варьирование признаков. Поэтому зависимость между биологическими признаками имеет не функциональный, а статистический характер, когда в массе однородных индивидов определенному значению одного признака, рассматриваемого в качестве аргумента, соответствует не одно и то же числовое значение, а целая гамма распределяющихся в вариационный ряд числовых значений другого признака, рассматриваемого в качестве зависимой переменной, или функции. Такого рода зависимость между переменными величинами называется корреляционной или корреляцией.

Функциональные связи легко обнаружить и измерить на единичных и групповых объектах, однако этого нельзя проделать с корреляционными связями, которые можно изучать только на групповых объектах методами математической статистики. Корреляционная связь между признаками бывает линейной и нелинейной, положительной и отрицательной. Задача корреляционного анализа сводится к установлению направления и формы связи между варьирующими признаками, измерению ее тесноты и, наконец, к проверке достоверности выборочных показателен корреляции.

Зависимость между переменными Y и X можно выразить аналитически (с помощью формул и уравнений) и графически (как геометрическое место точек в системе прямоугольных координат). График корреляционной зависимости строят по уравнению функции _x=f(x) или _у=f(у), которая со времен Гальтона получила название регрессии. Здесь _х и _у — средние арифметические, найденные при условии, что X или Y примут некоторые значения х или у. Эти средние называются условными. Регрессионному анализу посвящена следующая глава. Здесь же будут рассмотрены параметрические и непараметрические способы анализа линейных и нелинейных статистических связей.

ПАРАМЕТРИЧЕСКИЕ ПОКАЗАТЕЛИ СВЯЗИ

Коэффициент корреляции. Сопряженность между переменными величинами Y и X можно установить, сопоставляя числовые значения одной из них с соответствующими значениями другой. Если при увеличении одной переменной увеличивается другая, это указывает на положительную связь между этими величинами, и, наоборот, когда увеличение одной переменной сопровождается уменьшением значений другой, это указывает на отрицательную связь. Подобную взаимосвязь устанавливают при наличии однозначных отношений между переменными У и X, когда речь идет о приращении или уменьшении функции по заданным значениям аргумента. Иная ситуация наблюдается в случае варьирующих признаков. Здесь приходится исследовать собственно не приращение или уменьшение функции, а сопряженную вариацию (ковариацию), выражая ее в виде взаимно связанных отклонений вариант отих средних

Ковариация () есть усредненная величина произведений отклонений каждой пары наблюдений от их средних, т. е.. Очевидно, что величина этого показателя будет в значительной мере зависеть от того, насколько часто в общем ряду произведениебудет иметь один знак — плюс или минус.В первом случае пары вариант должны отклоняться от своих средних в одном направлении (т. е.иилии. В другом случае, если, тоили наоборот. При этом преобладание величин одного знака в принципе способствует большему абсолютному значению коэффициента ковариации, так как величины с разными знаками в сумме дают меньшую абсолютную величину. Среднее значение всех произведений указывает, в какой мере большим (или меньшим) значениямсоответствуют большие (или меньшие) значения.

Недостаток коэффициента ковариации заключается в том, что этот коэффициент не учитывает случаи, когда коррелируемые признаки выражаются разными единицами измерения. Например, масса тела может коррелировать с его линейными размерами, длина колосьев — с массой содержащихся в них зерен и т. д. Недостаток, присущий ковариации, устраняется, если вместо отклоненийиспользовать их отношения к средним

квадратическим отклонениями. В результате получается показатель, который называют эмпирическим коэффициентом корреляции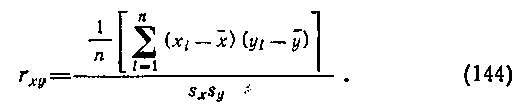

Коэффициент корреляции можно вычислить, не прибегая к расчету среденихквадратических отклонений, что упрощает вычислительную работу, по следующей аналогичной формуле:

Ё11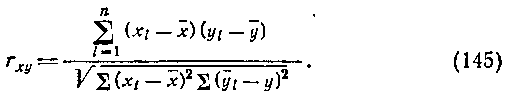

Коэффициент корреляции — отвлеченное число, лежащее в пределах от —1 до +1. При независимом варьировании признаков, когда связь между ними полностью отсутствует, г =0. Чем сильнее сопряженность между признаками, тем выше значение коэффициента корреляции. Следовательно, при | г | >0 этот показатель характеризует не только наличие, но и степень сопряженности между признаками. При положительной или прямой связи, когда большим значениям одного признака соответствуют большие же значения другого, коэффициент корреляции имеет положительный знак и находится в пределах от 0 до +1, при отрицательной или обратной связи, когда большим значениям одного признака соответствуют меньшие значения другого, коэффициент корреляции сопровождается отрицательным знаком и находится в пределах от 0 до —1.

Коэффициент корреляции нашел широкое применение в практике, но он не является универсальным показателем корреляционных связей, так как способен характеризовать только линейные связи, т. е. выражаемые уравнением линейной регрессии. При наличии нелинейной зависимости между варьирующими признаками применяют другие показатели связи,

о которых речь пойдет ниже.

Вычисление коэффициента корреляции. Это вычисление производят разными способами и по-разному в зависимости от числа наблюдений (объема выборки). Рассмотрим отдельно специфику вычисления коэффициента корреляции при наличии малочисленных выборок и выборок большого объема.

Малые выборки. При наличии малочисленных выборок коэффициент корреляции вычисляют непосредственно по значениям сопряженных признаков, без предварительной группировки выборочных данных в вариационные ряды. Для этого служат приведенные выше формулы (144) и (145). Более удобными, особенно при наличии многозначных и дробных чисел, которыми выражаются отклонения вариант я,- и г/* от средних хну, служат следующие рабочие формулы:











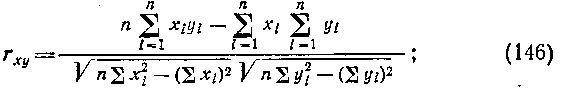
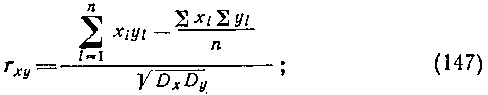
. МНОЖЕСТВЕННАЯ И ЧАСТНАЯ КОРРЕЛЯЦИЯ

Множественная корреляция. Наряду с анализом двумерных совокупностей в биологии широкое применение находит статистический анализ многомерных корреляционных связей. Простейшим случаем множественной корреляции является зависимость между тремя признаками: X, Y и Z. Тесноту связи одного из них (X) с двумя другими признаками (Y и Z) измеряют с помощью коэффициента множественной корреляции:






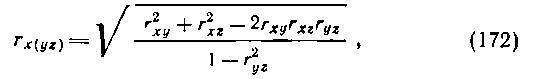
Где r_ху, r_хг и r_уг — коэффициенты линейной корреляции между парами признаков X и Y, X и Z, Y и Z.

Коэффициент множественной корреляции принимает значения от нуля до единицы (0≤r≤l). Значимость этого совокупного показателя корреляции оценивают по величине t-критерия Стьюдента с числом степеней свободы k=n—3 и принятым уровнем значимости.

Пример 18. Из снопа озимой ржи случайным способом было отобрано 10 колосьев. Затем измерили длину каждого колоса X, подсчитали число колосков Y и количество зерен Z в каждом колосе. Собранные данные и их первичная обработка приведены в табл. 115.

Чтобы определить коэффициент множественной корреляции между этими признаками, необходимо сначала рассчитать парные коэффициенты корреляции. Используя итоги табл. 115, на ходим суммы квадратов отклонений вариант отих средних арифметических, т. е. девиаты:







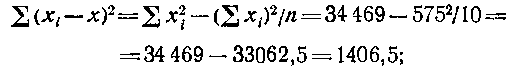
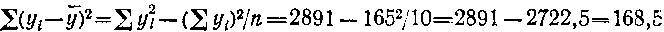
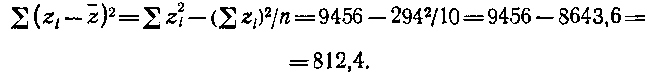
Таблица 115

Отсюда;

Затем рассчитываем величины сопряженной вариации:







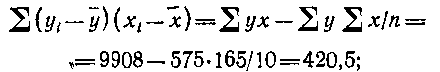
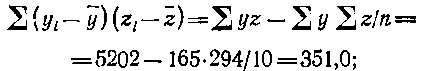
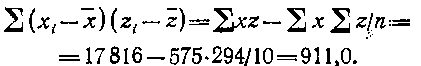
Наконец, определяем парные коэффициенты корреляции:







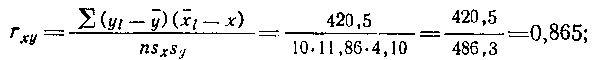
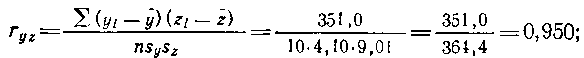
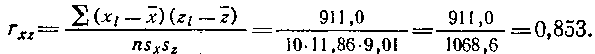
Подставляем известные величины в формулу (172):



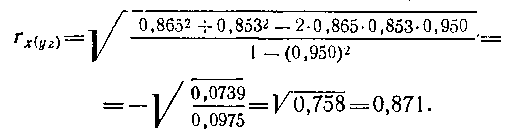
Критерий достоверности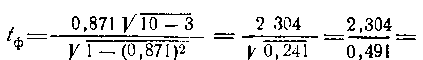

;дляи_ (см. табл. V Приложе

ний). Нулевая гипотеза отвергается на 1%-ном уровне значимости