Биометрия. Материалы для практического занятия. Предметом биометрии

• Название: Материалы для практического занятия. Предметом биометрии
• Анкор: Биометрия.docx
• Дата: 26.04.2017
• Размер: 1.29 Mb.
• Имя файла: Биометрия.docx
• Тип: Документы; #5939
• страница: 8 из 11

Частная корреляция.Если известна связь между признаками X, У и Z, можно определить частные или парциальные коэффициенты корреляции, показывающие корреляционную зависимость между двумя варьирующими признаками при постоянной величине третьего признака. Для определения частного коэффициента корреляции между признаками XиУ при постоянной величине признака Z применяют формулу



Заключение знака Z в скобки обозначает, что влияние признака Z на корреляцию между X и У исключено.

Соответственно формула для определения частного коэффициента корреляции между признаками X и Z при исключении влияния на эту связь признака У будет выглядеть так:



И наконец, частный коэффициент корреляции между признаками У и Z при постоянной величине признака X определяется по формуле



Тема № 5.Метод хи-квадрат

Цель– научиться применять критерий хи-квадрат.

Задачи. Функция χ².Число степеней свободы.Уровень значимости.Проверка независимости.Проверка гипотезы о равновесии Харди—Вайнберга.

Краткое содержание.

Полезным методом, позволяющим судить о том, соответствуют ли результаты экспериментов той или иной гипотезе, является метод хи-квадрат (χ²). Функция χ² определяется как

χ²=∑[(Н-О)²/О]

где Н-наблюдаемое значение, О-ожидаемое значение, а символ ∑ означает суммирование по всем сериям экспериментов.

Рассмотрим эксперимент, в котором Мендель скрещивал высокие растения (ТТ) с низкими (tt).В поколении F, скрещиваются гетерозиготыTtх Tt.Согласно гипотезе Менделя, в поколении F₂соотношение высоких (ТТ и Tt)и низких (tt)растений должно быть 3 :1. Было получено 787 высоких и 277 низких растений. Расчет значений хи-квадрат для этого эксперимента приведен в табл. П.1. В результате χ²= 0,59. Подтверждает ли это значение исходную гипотезу? Иными словами, можно ли разность между теоретически ожидаемой и реально наблюдаемой величинами отнести за счет случайности? Чтобы ответить на этот вопрос, мы должны познакомиться с двумя понятиями: число степеней свободы и уровень значимости (достоверности).

Число степеней свободы легко определить как число «классов», объемы которых должны быть известны, для того, чтобы подсчитать объемы всех классов исходя из общего объема выборки. В рассматриваемом примере число степеней свободы равно единице, так как если мы знаем объем одного класса (например, 787 высоких растений), то можем определить объем другого класса вычитанием объема первого класса из общего объема (1064 — 787 = 277). Вообще, в экспериментах

Таблица 1.П.1. Вычисление χ² для эксперимента Менделя с высокими и низкими растениями гороха





Таблица 2.П.1. Значения χ², соответствующие различным уровням значимости и степеням свободы

Число степеней		Уровень значимости
свободы	0,05	0,01	0,001
1	3,84	6,64	10,83
2	5,99	9,21	13,82
3	7,82	11,34	16,27
4	9,49	13,28	18,47
5	11,07	15,09	20,52
6	12,59	16,81	22,46
7	14,07	18,48	24,32
8	15,51	20,09	26,13
9	16,92	21,67	27,88
10	18,31	23,21	29,59

такого типа число степеней свободы на единицу меньше числа классов, т. е. k — 1, поскольку последний класс может быть подсчитан вычитанием суммы всех остальных классов из их общего числа. (Ниже мы увидим, что в экспериментах другого типа число степеней свободы может отличаться от k — 1.)

Уровень значимости отражает риск того, что мы отвергнем истинную гипотезу. Различия между ожидаемыми и наблюдаемыми значениями могут варьировать в силу случайных причин, но если вероятность того, что расхождение объясняется случайными причинами, очень мала, то гипотеза отвергается, хотя и не исключено, что она верна. Обычно в качестве уровня значимости выбирается значение 5%. Это означает, что гипотезу решено считать не соответствующей наблюдениям, если вероятность того, что расхождение между теоретически ожидаемыми и наблюдаемыми в эксперименте данными, обусловленное только случайными причинами, составляет не более 5%. Значения χ² для различного числа степеней свободы и уровней значимости 5, 1 и 0,1% приведены в табл. П.2.

Возвратимся к вопросу о том, соответствуют ли данные эксперимента Менделя его гипотезе. Значение χ² равно 0,59, степень свободы одна. Расхождение между теоретическими и экспериментальными значениями допустимо, поскольку оно меньше значения хи-квадрата для одной степени свободы и 5%-ного уровня значимости (последнее равно 3,84; см. табл. П.2). Следовательно, мы вправе утверждать, что данные эксперимента согласуются с гипотезой Менделя и что различие между ожидаемыми и наблюдаемыми значениями объясняются случайными причинами.



Таблица З.П.1. Вычисление χ^2. Для гипотезы независимого расщепления двух локусов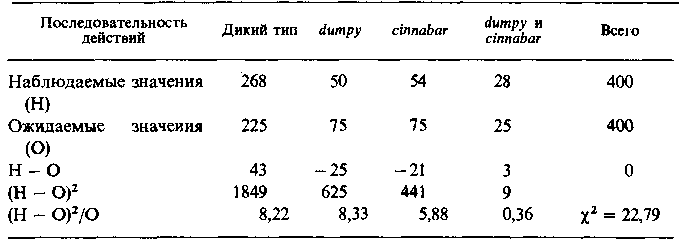



мух наблюдалось следующее распределение:

Дикий тип 268

Короткие крылья 50

Яркие глаза 54

Короткие крылья и яркие глаза 28

Нам нужно определить, соответствуют ли эти результаты гипотезе о независимости расщепления локусов. Расчет хи-квадрат приведен в табл. П.З. Число степеней свободы равно k —1 = 3, поскольку, зная число мух трех типов и общее число мух, мы можем определить число мух четвертого типа. Для трех степеней свободы значение хи-квадрат на 95% уровне значимости равно 7,82 (табл. П.2). Следовательно, мы должны отвергнуть гипотезу о независимом расщеплении. В данном случае мы должны были бы отвергнуть эту гипотезу даже на 99,9%-ном уровне значимости, поскольку на этом уровне при трех степенях свободы хи- квадрат равно 16,27.

Проверка независимости. Иногда желательно определить, зависят ли друг от друга результаты двух серий наблюдений над одними и теми же особями. Например, 256 пар близнецов классифицировались по двум признакам: монозиготность-дизиготность и конкордантность-дискордантность (в отношении бронхиальной астмы). Пара близнецов называется конкордантной, когда оба близнеца страдают этим заболеванием, и дискордантной, когда болен один из близнецов. Случаи, когда оба близнеца здоровы, из рассмотрения исключаются. Были получены следующие результаты:




В данном случае мы не располагаем никакой гипотезой, позволяющей нам рассчитать ожидаемые частоты для каждого класса, однако можно проверить, зависят ли друг от друга рассматриваемые признаки, с помощью следующей таблицы 2x2. Сначала составим таблицу наблюдаемых результатов:

Теперь мы можем рассчитать теоретически ожидаемые результаты для каждого из четырех классов, исходя из предположения, что тип близнецов и конкордантность - это независимые признаки. Для этого необходимо перемножить соответствующие значения в строке и столбце «всего» и поделить полученное число на общую сумму. Например, теоретически ожидаемое число монозиготных конкордантных близнецов равно (64 х 76)/256 = 19,00. Таблица теоретически ожидаемых значений имеет вид

Значение χ², рассчитанное так же, как и в предыдущем примере, равно 12,08. Хотя в данном случае имеются четыре класса, число степеней свободы тем не менее равно единице, а не трем. Это объясняется тем, что для определения всех четырех значений в таблице 2x2 нам достаточно, кроме значений в графах «всего», знать хотя бы одно из четырех. Например, число монозиготных дискордантных близнецов равно 64 — 30 = 34 и т. п. Такие таблицы могут иметь любое число строк (г) и столбцов (с). При этом, разумеется, строка и столбец «всего» не учитываются. В общем случае число степеней свободы равно (г — 1)(с — 1).

Поскольку значение χ² = 12,08 больше допустимого значения хи-квадрата для одной степени свободы и 5%-ного уровня значимости, мы приходим к заключению, что тип близнецов, с одной стороны, и конкордантность или дискордантность в отношении бронхиальной астмы-с другой, нельзя считать независимыми друг от друга. Отсутствие независимости, возможно, обусловлено существованием наследственной составляющей в предрасположенности к бронхиальной астме.

Проверка гипотезы о равновесии Харди—Вайнберга. У людей имеются два аллеля в локусе pGM. В выборке из 200 представителей белой расы обладатели различных генотипов распределились следующим образом: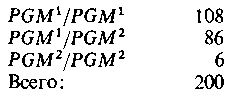






Мы хотим установить, соответствуют ли эти данные частотам, которых следует ожидать, исходя из равновесия Харди—Вайберга. Сначала рас считаем частоту раллеляPGM:

Р=[(108х2)+86]/400=302/400=0,755

Теоретически ожидаемые частоты и численность генотипов составляют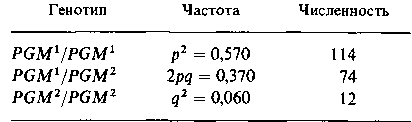

Рассчитывая значение хи-квадрат, как и выше, получаем χ² = 5,26. Каково число степеней свободы в этом случае? Оно равно единице, а не двум, как могло показаться по аналогии с рассмотренным выше случаем менделевского расщепления. Дело в том, что по исходным данным мы рассчитывали, что частота аллеляр равна 0,755. Зная это значение и общий объем выборки, мы можем определить ожидаемые численности двух генотипических классов, если знаем число особей в одном из этих трех классов.

Это позволяет сформулировать еще одно правило (аналогичное приведенному выше) для определения числа степеней свободы: число степеней свободы равно разности между числом классов и числом независимых величин, полученных на основе данных, использованных для расчета ожидаемых значений. В рассматриваемом выше случае менделевского расщепления общее число растений было единственным значением, полученным из исходных данных. Зная это значение и законы Менделя, мы можем рассчитать ожидаемое число растений каждого фенотипического класса. В случае проверки равновесия Харди—Вайнберга мы на основе исходных данных рассчитаем два значения: общее число людей в выборке и частоте аллеляр. Заметим, что величина χ², равная 5,26, статистически достоверна при 5%-ном уровне значимости и одной степени свободы, но статистически не достоверна для двух степеней свободы. Если бы мы ошибочно предположили, что существуют две степени свободы, то не отвергли бы гипотезу о соответствии частот указанных трех генотипов равновесию Харди—Вайнберга.

Предостережение. Метод хи-квадрат-это приблизительный метод, дающий хорошие результаты, только если общий объем выборки и теоретически ожидаемые численности в каждом классе достаточно велики; если же они малы, то данный метод неэффективен. Практически следует руководствоваться двумя правилами: 1) если имеется только одна степень свободы, то ожидаемые значения численности для каждого класса должны быть не меньше пяти; 2) если число степеней свободы больше единицы, то ожидаемые значения численности в каждом классе должны быть не меньше единицы. Существуют, однако, приемы, которыми можно воспользоваться, когда эти условия не выполняются.

Если число степеней свободы равно единице, а численность одного из классов меньше пяти, то следует применять поправку Йетса. Она состоит в том, что, прежде чем вычислить значения хи-квадрат, каждую из разностей между наблюдаемыми и ожидаемыми значениями приближают к нулю на 0,5 единицы. В табл. П.4 приведен расчет значения

Таблица 4.П.1. Вычисление χ² с учетом и без учета поправки Йетса для результатов возвратного скрещивания между кроликами-альбиносами (с^ас^а) и кроликами, гетерозиготными по гену альбинизма (с⁺с^а)




хи-квадрат для результатов возвратного скрещивания между кроликами-альбиносами (с^ас^а) и кроликами дикого типа, гетерозиготными по гену альбинизма (с ⁺ /с^а), без учета и с учетом поправки Йетса. Без учета поправки х²= 4, что означает статистическую достоверность при 5%-ном уровне значимости. С учетом поправки Йетса χ²= 3,06, что означает отсутствие статистической достоверности. Таким образом, мы приходим к заключению, что результаты эксперимента соответствуют ожидаемым.

Если число степеней свободы больше единицы, но имеются классы, в которых ожидаемые значения меньше единицы, то можно объединить эти классы таким образом, чтобы значения во всех новых классах были не меньше единицы. При этом не следует забывать о том, что при определении числа степеней свободы нужно использовать число новых (объединенных) классов. В табл. П.5 приводятся результаты исследования, в котором определялись хромосомные перестройки в выборке из 50 личинок Drosophilapseudoobscura. Прежде всего мы подсчитываем частоты каждой последовательности генов в популяции.

Таблица 5.П.1. Вычисление χ² с объединением и без объединения малочисленных классов при проверке равновесия Харди-Вайнберга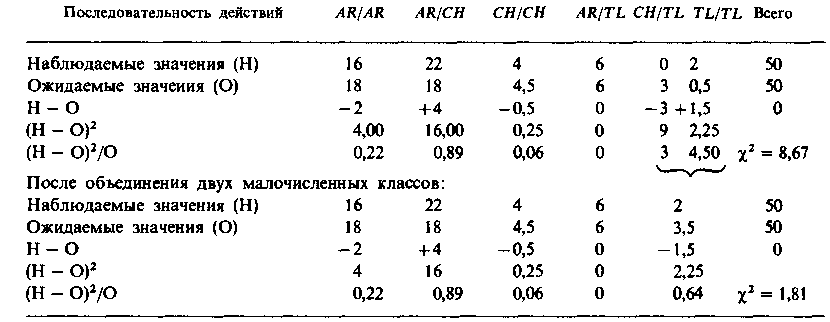






Ожидаемые частоты генотипов можно подсчитать путем разложения квадрата суммы (р + q + г)², ожидаемые численности генотипических классов получают умножением общего числа особей в выборке (50) на ожидаемые частоты. Все это проделано в табл. П.5. Из исходных данных определяют три независимые величины: частоты р, q(г не является независимой величиной, а рассчитывается просто как разность г = I — p — q) и общее число особей. Поскольку имеется шесть классов, число степеней свободы равно 6 — 3 независимых значения = 3. Величина χ² составляет 8,67, что статистически достоверно для 5%-ного уровня значимости и трех степеней свободы. В нижней части табл. П.5 два класса с минимальными ожидаемыми значениями объединены. Теперь мы имеем пять классов и, следовательно, 5 — 3 = 2 степени свободы. Новое значение χ² равно 1,81, что означает отсутствие статистической достоверности на 5%-ном уровне значимости.

Тема № 6.Статистические гипотезы и их проверка

Цель–научиться применять t-критерий Стьюдента, F-критерий Фишера.

Задачи.Параметрические критерии. t-критерий Стьюдента (t-распределение).Оценка разности средних. Оценка средней разности между выборками с попарно связанными вариантами. Ошибка средней разности. Оценка разности между выборочной и генеральной долями.F-критерий Фишера (F-распределение).

Краткое содержание. Ниже будут обсуждаться сравнительные оценки генеральных параметров по разности, наблюдаемой между сравниваемыми выборками. Это важно, так как ни одно исследование не обходится без сравнений. Сравнивать приходится данные опыта с контролем, урожайность одной культуры с урожайностью другой, продуктивность одной группы животных с продуктивностью другой и т. д.

О преимуществе той или иной из сравниваемых групп судят обычно по разности между средними долями и другими выборочными показателями — величинами случайными, сопровождаемыми ошибками репрезентативности.

Вопрос о достоверности выборочной разности с ее ошибкой приходится решать исходя из той или иной гипотезы, т. е. предположения или допущения относительно параметров сравниваемых групп, которое выражено в терминах вероятности и может быть проверено по выборочным характеристикам.

В области биометрии широкое применение получила так называемая нулевая гипотеза (Н₀). Сущность ее сводится к предположению, что разница между генеральными параметрами сравниваемых групп равна нулю и что различия, наблюдаемые между выборочными характеристиками, носят не систематический, а исключительно случайный характер. Так, если одна выборка извлечена из нормально распределяющейся совокупности с параметрамии, а другая — из совокупности с параметрамии, то нулевая гипотеза исходит из того, чтои, т. е.и(отсюда и на

звание гипотезы — нулевая).

Противоположная нулевой — альтернативная гипотеза (Н_а) — исходит из предположения, чтои

Для проверки принятой гипотезы, а следовательно, и достоверности оценки генеральных параметров по выборочным данным используют величины, функции распределения которых известны. Эти величины, называемые критериями достоверности, позволяют в каждом конкретном случае выявить, удовлетворяют ли выборочные показатели принятой гипотезе. Функции распределения указанных величин табулированы, т. е. сведены в специальные таблицы, где содержатся значения функции для разных чисел степеней свободы k или объема выборки п и уровней значимости

Уровень значимости, или вероятность ошибки, допускаемой при оценке принятой гипотезы, может различаться. Обычно при проверке статистических гипотез принимают три уровня значимости: 5%-ный (вероятность ошибочной оценки Р = 0,05), 1%-ный (Р = 0,01) и 0,1%-ный (Р = 0,001). В биологических исследованиях часто считают достаточным 5%-ный уровень значимости. При этом нулевую гипотезу не отвергают, если в результате исследования окажется, что вероятность ошибочности оценки относительно правильности принятой гипотезы превышает 5%, т. е.Если жето принятую гипотезу следует отвергнуть на взятом уровне. Ошибка при этом возможна не более чем в 5% случаев, т. е. она маловероятна.

При более ответственных исследованиях уровень значимости может быть уменьшен до 1 или даже до 0,1%. Трем упомянутым уровням значимостиотвечают (при нормальности распределения используемого критерия) нормированные отклонения ( t ): при(Р = 0.05) нормированное отклонение при(Р=0,01)—при('Р = 0,001)—I; и

соответственно пороги доверительной вероятности равны P₁ = 0,95, Р₂ = 0,99 и Р₃ = 0,999.

В области биометрии применяют два вида статистических критериев: Iпараметрические, построенные наосновании параметров данной совокупности (например,и) и представляющие функции этих параметров, и непараметрические, представляющие собой функции, зависящие непосредственно от вариант данной совокупности с их частотами. Первые служат для проверки гипотез о параметрах совокупностей, распределяемых по нормальному закону, вторые — для проверки рабочих гипотез независимо от формы распределения совокупностей, из которых взяты сравниваемые выборки. Применение параметрических критериев связано с необходимостью вычисления выборочных характеристик — средней величины и показателей вариации, тогда как при использовании непараметрических критериев такая необходимость отпадает.

При нормальном распределении признака параметрические критерии обладают большей мощностью, чем непараметрические критерии. Они способны более безошибочно отвергать нулевую гипотезу, если она не верна. Поэтому во всех случаях, когда сравниваемые выборки взяты из нормально распределяющихся совокупностей, следует отдавать предпочтение параметрическим критериям.

В случае очень больших отличий распределений признака от нормального вида следует применять непараметрические критерии, которые в этой ситуации оказываются часто более мощными. В ситуациях, когда варьирующие признаки выражаются не числами, а условными знаками, применение непараметрических критериев оказывается единственно возможным.

Из параметрических критериев в биометрии применяют t-критерий Стьюдента и F-критерий Фишера. Первый используют для сравнительной оценки средних величин, второй — для оценки дисперсий. Ниже рассмотрен отдельно каждый из этих критериев.

Параметрические критерии