Биометрия. Материалы для практического занятия. Предметом биометрии

Название	Материалы для практического занятия. Предметом биометрии
Анкор	Биометрия.docx
Дата	26.04.2017
Размер	1.29 Mb.
Формат файла
Имя файла	Биометрия.docx
Тип	Документы #5939
страница	3 из 11

1 2 3 4 5 6 7 8 9 10 11

Таблицы. Наиболее распространенной формой группировки являются статистические таблицы; они бывают простыми и сложными. К простым относятся, например, четырехпольные таблицы, применяемые при альтернативной группировке, когда одна группа вариант противопоставляется другой; например, здоровые — больным, высокие — низким и т. д. В качестве примера такой группировки могут служить результаты обследования 265 учащихся младших классов на состояние нёбных миндалин (табл. 1).

Таблица 1

Обнаружено детей

Школьные классы

Всего

здоровых

больных

Третьи и четвертые

63

92

155

Пятые и шестые

71

39

110

Всего

134

131

265

Из табл. 1 видно, что заболевание нёбных миндалин, по-видимому, чаще встречается среди учащихся третьих и четвертых классов.

К сложным относятся многопольные таблицы, применяемые при изучении корреляционной зависимости и при выяснении причинно-следственных отношений между варьирующими признаками. Примером корреляционной таблицы служат классические данные Гальтона, показывающие наличие положительной зависимости между ростом родителей и ростом их детей (табл. 2).

В качестве примера группировки, применяемой при выяснении причинно-следственных отношений между признаками, приведены данные, полученные в Научно-исследовательском институте имени В. В. Докучаева при испытании гречихи сорта «Богатырь» на урожайность в зависимости от предшественников табл. 3.

Богатырь» на урожайность в зависимости от предшественников (табл. 3).

Таблица 2.

Рост

родителей,

дюймы

Рост детей, дюймы

Всего

60,7

62,7

64,7

66,7

68,7

70,7

72,7

74,7

74

4

4

72

1

4

11

17

20

6

62

70

1

2

21

48

83

66

22

8

251

68

1

15

56

130

148

69

11

430

66

1

15

19

56

41

11

1

144

64

2

7

10

14

4

37

Всего

5

39

107

255

387

163

58

14

928

Из табл. 3 ясно, что в данных условиях лучшим предшественником для гречихи является, по-видимому, ячмень.

Таблица 3

Предшественники

Урожай гречихи по повторностям, ц/га

Средний

урожай

I

2

3

Горох раннезеленый

23,7

20,1

20,5

21,4

Чечевица

23,6

25,1

21,1

23,2

Чина степная № 21

26,7

23,2

23,8

24,6

Ячмень

26,0

24,9

25,3

25,4

Приведенными таблицами не исчерпывается их многообразие. Здесь рассмотрены лишь типичные для курса биометрии примеры. Из этих примеров видно, что статистические таблицы имеют не только иллюстративное, но и аналитическое значение, позволяя обнаруживать связи между варьирующими признаками.

Статистические ряды. Особую форму группировки представляют так называемые статистические ряды. Статистическим называется ряд числовых значений признака, расположенных в определенном порядке. В зависимости от того, какие признаки изучаются, статистические ряды делят на атрибутивные, вариационные, ряды динамики и регрессии, а также ряды ранжированных значений признаков и ряды накопленных частот, являющихся производными вариационных рядов. Примером атрибутивного ряда могут служить данные, показывающие зависимость между содержаниемгемоглобина Нb в крови и высотой организации позвоночных животных:

$c:\docume</h2>1\1\locals</h2>1\temp\finereader11\media\image1.jpeg$

Среди группировок видное место занимают вариационные ряды. На их описании следует остановиться более подробно. Ряды регрессии, динамики и другие будут рассмотрены в последующих главах.

Вариационным, рядом или рядом распределения называют двойной ряд чисел, показывающий, каким образом числовые значения признака связаны с их повторяемостью в данной статистической совокупности. Например, из урожая картофеля, собранного на одной из опытных делянок, случайным способом, т. е. наугад, отобрано 25 клубней, в которых подсчитывали число глазков. Результаты подсчета оказались следующие: 6, 9, 5, 7, 10, 8, 9, 10, 8, 11, 9, 12, 9, 8, 10, 11, 9, 10, 8, 10, 7, 9, 11, 9, 10. Чтобы разобраться в этих данных, расположим их в ряд (в порядке регистрации результатов наблюдений) с учетом повторяемости вариант в этой совокупности:

$c:\docume</h2>1\1\locals</h2>1\temp\finereader11\media\image2.jpeg$

Это и есть вариационный ряд. Числа, показывающие, сколько раз отдельные варианты встречаются в данной совокупности, называются частотами или весами вариант и обозначаются строчной буквой латинского алфавита f. Общая сумма частот вариационного ряда равна объему данной совокупности, т. е.

$c:\docume</h2>1\1\locals</h2>1\temp\finereader11\media\image3.jpeg$ (греческая буква сигма прописная) обозначает действие суммирования, в данном случае суммирование частот вариационного ряда от первого $c:\docume</h2>1\1\locals</h2>1\temp\finereader11\media\image4.jpeg$ класса, а п — общее число наблюдений, или объем совокупности.

Частоты (веса) выражают не только абсолютными, но и относительными числами — в долях единицы или в процентах от общей численности вариант, составляющих данную совокупность. В таких случаях веса называют относительными частотами или частостями. Общая сумма частостей равна единице, т. е.

$c:\docume</h2>1\1\locals</h2>1\temp\finereader11\media\image5.jpeg$ , если частоты выражены в процентах от общего числа наблюдений п. Замена частот частостями не обязательна, но иногда оказывается полезной и даже необходимой в тех случаях, когда приходится сопоставлять друг с другом вариационные ряды, сильно отличающиеся по их объемам.

Распределение исходных данных в вариационный ряд преследует определенные цели. Одна из них — ускорение работы при вычислении по вариационному ряду обобщающих числовых характеристик— средней величины и показателей вариации. Другая сводится к выявлению закономерности варьирования учитываемого признака. Приведенный ряд удовлетворяет первой, но не удовлетворяет достижению второй цели. Чтобы ряд распределения полностью удовлетворял предъявляемым к нему требованиям, его нужно строить по ранжированным значениям признака.

Под ранжированием (от франц. $c:\docume</h2>1\1\locals</h2>1\temp\finereader11\media\image6.jpeg$ —выстраивать в ряд по ранжиру, т. е. по росту) понимают расположение членов ряда в возрастающем (или убывающем) порядке. Так, в данном случае результаты наблюдений следует распределить так:

$c:\docume</h2>1\1\locals</h2>1\temp\finereader11\media\image7.jpeg$

Этот упорядоченный ряд распределения в равной мере удовлетворяет достижению и первой, и второй целей. Он хорошо обозрим и наилучшим образом иллюстрирует закономерность варьирования признака.

В зависимости от того, как варьирует признак — дискретно или непрерывно, в широком или узком диапазоне, — статистическая совокупность распределяется в безынтервальный или интервальный вариационные ряды. В первом случае частоты относятся непосредственно к ранжированным значениям признака, которые приобретают положение отдельных групп или классов вариационного ряда, во втором — подсчитывают частоты, относящиеся к отдельным промежуткам или интервалам (от — до), на которые разбивается общая вариация признака в пределах от минимальной до максимальной варианты данной совокупности. Эти промежутки, или классовые интервалы, могут быть равными и не равными по ширине. Отсюда различают равно- и неравноинтервальные вариационные ряды. Примером неравноинтервального ряда распределения могут служить данные А. Ф. Ковшарь (1966), показывающие зависимость между числом стай сизых голубей и количеством особей в стае в гнездовой (с 15 марта по 15 августа) и послегнездовой (с 15 августа по 15 марта) периоды их жизни (табл. 4).

В неравноинтервальных рядах характер распределения частот меняется по мере изменения ширины классовых интервалов. Поэтому в качестве числовых характеристик таких рядов используют особые показатели.

Неравноинтервальную группировку в биологии применяют сравнительно редко. Как правило, биометрические данные распределяются в равноинтервальные ряды, что позволяет не только выявлять закономерность варьирования, но и облегчает вычисление сводных числовых характеристик вариационного ряда, сопоставление рядов распределения друг с другом.

Таблица 5

Число наблюдений п (от —до)

Число классов

К

25-40

5-6

40—60

6-8

60-100

7—10

100—200

8—12

>200

10-15

Приступая к построению равноинтервального вариационного ряда, важно правильно наметить ширину классового интервала. Дело в том, что грубая группировка (когда устанавливают очень широкие классовые

Таблица 4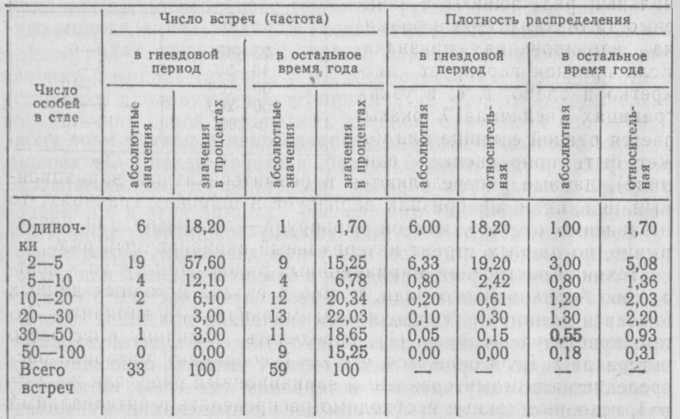

$c:\docume</h2>1\1\locals</h2>1\temp\finereader11\media\image1.jpeg$

интервалы) искажает типичные черты варьирования и ведет к снижению точности числовых характеристик ряда. При выборе чрезмерно узких интервалов точность обобщающих числовых характеристик повышается, но ряд получается слишком растянутым и не дает четкой картины варьирования.

Для получения хорошо обозримого вариационного ряда и обеспечениядостаточной точности вычисляемых по нему числовых характеристик следует разбить вариацию признака (в пределах от минимальной до максимальной варианты) на такое число групп или классов, которое удовлетворяло бы обоим требованиям. Эту задачу решают делением размаха варьирования признака на число групп или классов, намечаемых при построении вариационного ряда:

$c:\docume</h2>1\1\locals</h2>1\temp\finereader11\media\image2.jpeg$ (1)

где— величина классового интервала; $c:\docume</h2>1\1\locals</h2>1\temp\finereader11\media\image4.jpeg$ — максимальная и минимальная варианты совокупности; К — число классов, на которые следует разбить вариацию признака.

Число классов (К) можно приблизительно наметить, пользуясь табл. 5.

Более точно величинуК можно определить по формуле Стерджеса: $c:\docume</h2>1\1\locals</h2>1\temp\finereader11\media\image5.jpeg$ При наличии в совокупности большого числа членов $c:\docume</h2>1\1\locals</h2>1\temp\finereader11\media\image6.jpeg$ можно использовать формулуК $c:\docume</h2>1\1\locals</h2>1\temp\finereader11\media\image7.jpeg$ .

Вопрос о том, распределять ли собранные данные в интервальный или безынтервальный ряд, решают в зависимости от характера и размаха варьирования признака.

Если признак варьирует дискретно и слабо, т. е. в узких границах (величинаК оказывается равной единице или может быть приравнена к единице), данные распределяются в безынтервальный вариационный ряд. Если же признак варьирует в широких границах, то независимо от того, как он варьирует — дискретно или непрерывно, по данным строят интервальный вариационный ряд.
1 2 3 4 5 6 7 8 9 10 11