Биометрия. Материалы для практического занятия. Предметом биометрии
 Скачать 1.29 Mb.
|
Техника построения вариационных рядов. Приступая к пост роению вариационного ряда, нужно в сводке исходных данных отыскать минимальнуюи максимальнуюварианты. За тем, используя формулу (1), определить величину классового интервала. Если окажется, что, собранный материал рас пределяется в безынтервальный вариационный ряд; если же, исходные данные необходимо распределять в интервальный ряд. При этом точность величины классового интервала должна соответствовать точности, принятой при измерении признака. Например, жирномолочность коров (я=60), содержащихся на ферме, варьирует от 3,21 до 4,55%. В таком случае классовый интервал устанавливается следующим образом:  Если точность измерения данного признака ограничить десятыми долями единицы, величина классового интервала окажется сле дующей:  В обоих случаях результаты наблюдений должны распределяться в интервальный вариационный ряд. При построении интервального вариационного ряда следует поступать так, чтобы минимальная варианта совокупности попа дала примерно в середину первого классового интервала. Выпол нение этого требования гарантирует построение вариационного ряда, наиболее полно отвечающего природе изучаемого явления, а следовательно, и наименьшие потери информации о точности вычисляемых статистических характеристик ряда. Этому требо ванию удовлетворяет формула  где—нижняя граница первого классового интервала;— минимальная варианта исследуемой совокупности;—величина классового интервала. Так, при  нижняя граница первого класса Прибавив к этой величине = 0,19, определяем верхнюю границу первого класса: 3,12+ +0,19=3,31. Затем находим верхнюю границу второго класса: 3,31+0,19 = 3,50 и т. д., пока не получим интервал, в который попадает максимальная варианта совокупности .Наметив классовые интервалы, остается распределить по ним все варианты совокупности, т. е. определить частоты каждого класса. Тут, однако, возникает вопрос: в какие классы относить варианты, которые по своей величине совпадают с верхней гра ницей одного и нижней границей другого, соседнего класса? Например, в какой класс следует отнести варианту 3, 31 — в пер вый или во второй? Этот вопрос решается по-разному. Можно помещать в один и тот же класс варианты, которые больше ниж ней, но меньше или равны его верхней границе, т. е. по принципу «от и до включительно». Чаще, однако, поступают таким обра зом: верхние границы классов уменьшают на величину, равную точности, принятой при измерении признака, чем и достигается необходимое разграничение классов. Следующий шаг ведет к замене классовых интервалов на их центральные или срединные значения. В результате интерваль ный вариационный ряд превращается в безынтервальный ряд. Необходимость такой замены вызывается тем, что обобщающие числовые характеристики (средняя, дисперсия и др.) вычисляют ся по безынтервальный рядам. Срединные значения классовых интервалов Xi, как это следует из формулы (2), отстоят от их нижних границ хв на величину, равную половине классового ин тервала. Наиболее точно центральную величину классового интервала можно получить по формуле  где—конечная точка интервала, равная  т. е. началу следующего класса, уменьшенному на точность измерения приз нака.Середины классов приобретают значения отдельных вари ант и называютсяклассовыми вариантами в отличие от кон кретных вариант, составляющих данную совокупность. Описанную методику можно продемонстрировать на конкретных при мерах. Пример 1. На свиноферме зарегистрировано 64 опороса. Ко личество поросят, полученных от каждой свиноматки, варьиро вало следующим образом:  В этой совокупности хmin и хmaxОтсюда  Так как признак варьирует дискретно и, совокупность наблюдений следует распределить в безынтервальный вариаци онный ряд, т. е. непосредственно по ранжированным значени ям признака, которые и будут классами данного ряда. Чтобы при определении частот каждого класса не.сбиться со счета, нужно построить вспомогательную (расчетную) таб лицу, в которой первая графа заполняется классами (в данном случае ранжированными значениями признака), а вторая — служит для учета частот, распределяемых по этим классам. Разноску частот по классам производят следующим обра зом. Просматривая сводку результатов наблюдений, во второй графе расчетной таблицы с помощью условных знаков отмеча ют повторяемость вариант для каждого класса. При этом ре комендуется не выискивать одинаковые варианты в общей сово купности чисел, а разносить их по классам, что не одно и то же. Пренебрежение этой рекомендацией приводит к ошибкам, лишней затрате труда и времени на выполнение работы. Услов ными знаками при разноске наблюдений по классам могут быть точки, черточки и другие условные знаки. Удобным, особенно при обработке больших совокупностей, оказывается следующий шифр частот:  Наилучшим способом разноски вариант является расклад ка бланков, каждый из которых соответствует отдельному наб людению и содержит значения признаков. В этом случае зна чения признака, попадающие в один класс ряда, образуют от дельную стопку бланков. Всего таких стопок окажется столь ко, сколько образовано интервалов вариационного ряда. После окончания разноски ее результаты можно неоднократно прове рить просмотром каждой из стопок бланков, т. е. просмотром тех вариант, которые попали в каждый класс ряда. Это позво ляет полностью исключить ошибки, возможные при иных спо собах подсчета классовых частот. Закончив разноску вариант по классам, переводят шифр частот в числа. В результате получается третья графа вспомо гательной таблицы, содержащая частоты безынтервального ва риационного ряда (табл. 6). Таблица 6 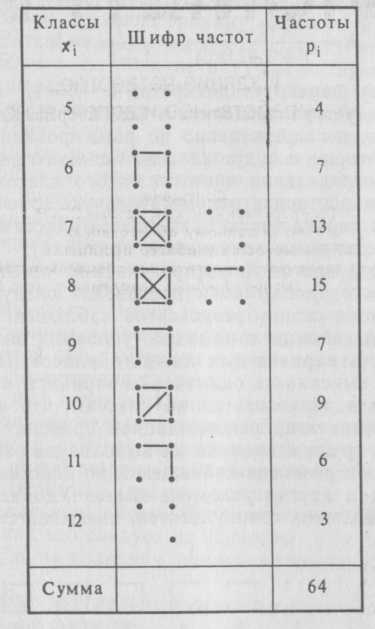 Полученный вариационный ряд выражает зависимость меж ду отдельными вариантами и частотой их встречаемости в дан ной совокупности, т. е. закономерность варьирования учитывае мого признака. Пример 2. На основании многолетних клинических наблю дений, проводившихся в Сухумском питомнике обезьян, состав лена следующая выборка, включающая 100 анализов на содер жание кальция (мг%) в сыворотке крови низших обезьян (павианов-гамадрилов):
Нужно сгруппировать эти данные в вариационный ряд. В данном случае признак варьирует непрерывно в пределах от 9,0 до 14,7 мг%. Устанавливаем величину классового интер вала:  Так как выборку приходится группировать в интервальный вариационный ряд, определяем нижнюю границу первого класса:  Затем намечаем следующие классовые интервалы:   Получилось восемь ин тервалов. Разграничиваем их на величину, равную точности из мерения признака, т. е. уменьшаем верхние границы интервалов на 0,1 мг%. Строим вспомогательную расчетную таблицу и раз носим все 100 вариант по намеченным классовым интервалам (табл. 7).Переводим шифр частот в числа, сумма которых должна быть равна объему данной выборки, т. е  . В резуль тате получается интервальный вариационный ряд.Срединные значения классов, приведенные в табл. 7, полу чены прибавлением к нижним границам классов ½ классово го интервала — величины, равной  , т. е., по формуле (3), и т. д. Таким образом, интервальный вариационный ряд превращен в ряд безынтервальный.Пример 3. В результате учета яйценоскости 80 кур, содер жащихся на птицеферме, было установлено, что признак варь ирует от 208 до 250 яиц, полученных от несушки за 1 год. Оп ределяем классовый интервал:  Так как классовый интервал не равен единице, результаты на блюдений нужно распределять в интервальный вариационный ряд, несмотря на то что признак варьирует дискретно. Уста навливаем нижнюю границу первого класса: 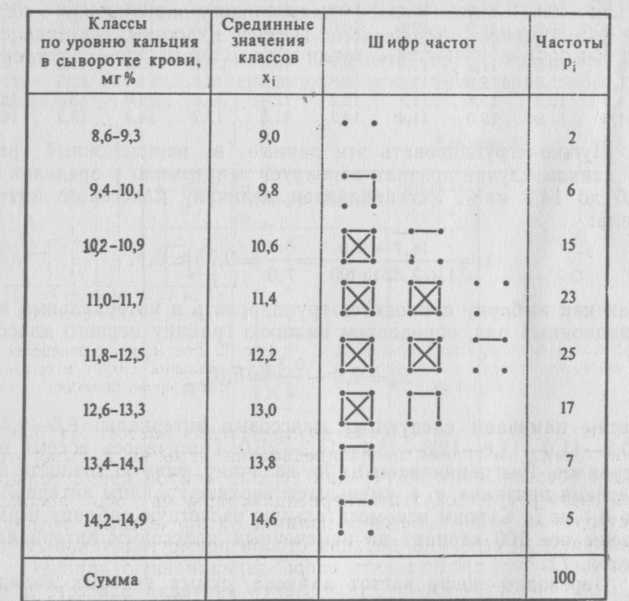 205. Намечаем классовые интервалы:   , Уменьшаем верхние границы классов на единицу:  Дальнейшие действия, относя щиеся к построению вариационного ряда, понятны из предыду щих примеров. |