Биометрия. Материалы для практического занятия. Предметом биометрии

• Название: Материалы для практического занятия. Предметом биометрии
• Анкор: Биометрия.docx
• Дата: 26.04.2017
• Размер: 1.29 Mb.
• Имя файла: Биометрия.docx
• Тип: Документы; #5939
• страница: 6 из 11

Коэффициент вариации. Дисперсия и среднее квадратическое отклонение применимы и для сравнительной оценки одноименных средних величин. В практике же довольно часто приходится сравнивать изменчивость признаков, выраженных разными единицами. В таких случаях используют не абсолютные, а относительные показатели вариации. Дисперсия и среднее квадратическое отклонение как величины, выражаемые теми же единицами, что и характеризуемый ими признак, для оценки изменчивости разноименных величин непригодны. Одним из относительных показателей вариации является коэффициент вариации. Этот показатель представляет собой среднее квадратическое отклонение, выраженное в процентах от величины средней арифметической:



Пример 13. Сравнивают два варьирующих признака. Один характеризуется средней=2,4 кг и средним квадратическим отклонением=0,58 кг, другой — величинами=8,3 см и = 1,57 см. Следует ли отсюда, что второй признак варьирует сильнее, чем первый? Нет, не следует, так как среднее квадратическое отклонение определяют по отклонениям от средних, а они различны по величине. Кроме того, не вполне корректно сравнивать величины, выраженные разными единицами меры. Именно поэтому в подобных случаях уместно использовать безразмерные значения коэффициентов вариации. Сравнивая их в приводимом примере, находим, что сильнее варьирует не второй, а первый признак:



Различные признаки характеризуются различными коэффициентами вариации. Но в отношении одного и того же признака значение этого показателяостается более или менее устойчивым и при симметричных распределениях обычно не превышает 50%. При сильно асимметричных рядах распределения коэффициент вариации может достигать 100% и даже выше. Варьирование считается слабым, если не превосходит 10%, средним, когдасоставляет 11—25%, и значительным при



Применяя коэффициент вариации в качестве характеристики варьирования, следует учитывать единицы размерности изучаемого признака: линейные или весовые (объемные). Акад. И. И. Шмальгаузен (1936) отмечал, что в таких случаях коэффициент вариации оказывается неодинаковым. Иллюстрацией тому могут служить данные Ю. Г. Артемьева (1939), исследовавшего варьирование величины внутренних органов у малых сусликов в зависимости от того, какими единицами меры выражены признаки (табл.10).

Данные, приведенные в табл. 10, показывают, что при линейном выражении величины признака коэффициент вариации оказывается примерно в три раза меньше, чем При кубическом выражении того же признака. Причина такого явления — в математических свойствах, которые надо учитывать, чтобы избежать возможных ошибок.

Таблица 10.

Органы	Коэффициент вариации при разном выражении признаков
	линейном	кубическом
Сердце	3,4	10,2
Легкие	9,6	29,5
Селезенка	9,8	29,8
Почка	3,1	9,4
Печень	3,0	9,3

Нормированное отклонение t.Отклонение той или иной варианты от средней арифметической, отнесенное к величине среднего квадратического отклонения, называют нормированным отклонением-.



Этот показатель позволяет «измерять» отклонения отдельных вариант от среднего уровня и сравнивать их для разных признаков.

Пример 14. При обследовании группы подростков в возрасте от 15 до 16 лет установлено, что средний рост юношей характеризуется следующими показателями:=164,8 см и= = 5,8 см. В группе оказался юноша, рост которого равен 172,4 см. Спрашивается: как велико отклонение роста этого юноши от средней величины данного признака в этой группе?

Нормируя рост юноши (=172,4), находим = + 1,31.

Получая значения нормированных отклонений для разных признаков, можно сравнить места, занимаемые особью, индивидом и т. п. по каждому из этих признаков в их распределениях. Пусть, например, нормированное -отклонение у рассматриваемого юноши по ширине плеч равно — 0,41. Тогда можно утверждать что у него длина тела отклоняется от средней в сторону больших величин этого признака, а ширина плеч — в сторону малых, т. е. характерен относительно узкоплечий тип телосложения.

Нормированное отклонение используют также при работе с так называемым нормальным распределением.

СТРУКТУРНЫЕ СРЕДНИЕ И СПОСОБЫ ИХ ВЫЧИСЛЕНИЯ

Медиана (Me). Средняя арифметическая — одна из основных характеристик варьирующих объектов по тому или иному признаку. Однако она не лишена недостатков, так как очень чувствительна к увеличению числа наблюдений или к уменьшению за счет вариант, резко отличающихся по своей величине от основной массы. Поэтому на величину средней арифметической могут значительно влиять крайние члены ранжированного вариационного ряда, которые как раз и наименее характерны для данной совокупности. В связи с этим во многих случаях в качестве обобщающих характеристик совокупности более полезными могут оказаться так называемые структурные средние. Эти величины обычно представляют собой конкретные варианты имеющейся совокупности, которые занимают особое место в ряду распределения.

Одной из таких характеристик является медиана — средняя, относительно которой ряд распределения делится на две равные части: в обе стороны от медианы располагается одинаковое число вариант. При наличии небольшого числа вариант медиана определяется довольно просто. Для этого собранные данные ранжируют, и при нечетном числе членов ряда центральная варианта и будет его медианой. При четном числе членов ряда медиана определяется по полусумме двух соседних вариант, расположенных в центре ранжированного ряда. Например, для ранжированных значений признака —12 14 16 18 20 22 24 26 28 — медианой будет центральная варианта, т. е. Me—20, так как в обе стороны от нее отстоит по четыре варианты. Для ряда с четным числом членов — 6 8 10 12 14 16 18 20 22 24 — медианой будет полусумма его центральных членов, т. е. Me— (14+16)/2= 15.

Для данных, сгруппированных в вариационный ряд, медиана определяется следующим образом. Сначала находят класс, в котором содержится медиана. Для этого частоты ряда кумулируют в направлении от меньших к большим значениям классов до величины, превосходящей половину всех членов данной совокупности, т. е. n/2. Первая величина в ряду накопленных частот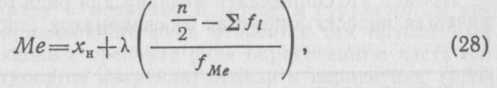, которая превышает, соответствует медианному классу. Затем берут разность междуи суммой накопленных частот, предшествующей медианному классу, которая относится к частоте медианного класса; результат умножают на величину классового интервалаНайденную таким способом величину прибавляют к нижней границемедианного класса. Если же исходные данные распределены в безынтервальный вариационный ряд, названную величину прибавляют к полусуммесоседних классовых вариант. В результате получается искомая величина медианы. Описанные действия выражаются в виде следующей формулы:



где—нижняя граница классового интервала, содержащего медиану, или полусумма соседних классов безынтервального ряда, в промежутке между которыми находится медиана;— сумманакопленных частот, стоящая перед медианным классом;— частота медианного класса;—величина классового интервала;—общее число наблюдений.

Пример 20. Вернемся к ряду распределения кальция (мг%) в сыворотке крови обезьян и вычислим для него медиану (табл. 17).


Таблица 17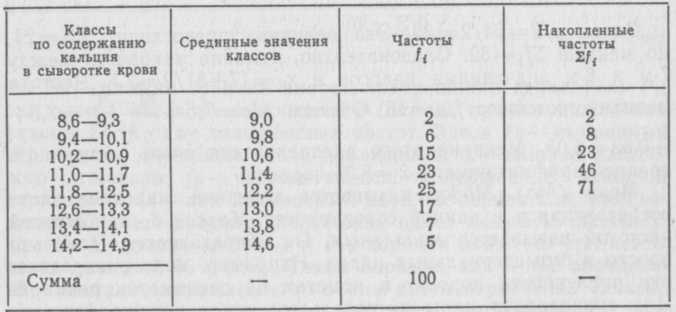





В данном случае=100/2=50. Эта величина больше = 46, но меньше=71. По=71 определяем интервал, в котором находится медиана. Границы этого интервала: нижняя= 11,8 и верхняя х_в=12,5; его частота=25. Классовый интервал=0,8. Подставляя эти величины в формулу (28), находим



Теперь превратим интервальный вариационный ряд в безынтегральный и вычислим медиану по срединным значениям классовых интервалов. Медиана находится между значениями классов 11,4 и 12,2. Отсюда

Пример 21. Определить медиану для ряда распределения количества поросят в пометах 64 свиноматок (табл. 18).


Таблица 18





Здесь=64/2=32. Эта величина превосходит=24, но меньше .=39. Следовательно, медиана находится между 7-м и 8-м значениями классов и= (7+8)/2=7,5. Частота

медианного класса=15. Отсюда

+Медиана этого распределения очень близка к

средней арифметической=8,25 поросят.

Мода (Мо). Модой называется величина, наиболее часто встречающаяся в данной совокупности. Класс с наибольшей частотой называется модальным. Он определяется довольно просто в безынтервальных рядах. Например, мода распределения численности поросят в пометах 64 свиноматок равна 8. Для определения моды интервальных рядов служит формула



где—нижняя границамодального класса, т. е. класса с наибольшей частотой;—частота класса, предшествующего

модальному;—частота класса, следующего за модальным; — ширина классового интервала.

Пример 22. Определить моду ряда распределения кальция (мг%) в сыворотке крови обезьян. Необходимые данные содержатся в табл. 17. Частота модального класса=25, его нижняя граница=11,8. Частота класса, предшествующего модальному,=23, частота класса, следующего за модальным, = 17;=0,8. Подставляя эти данные в формулу (29), находим



Квантили. Наряду с медианой и модой к структурным характеристикам вариационного ряда относятся так называемые квантили, отсекающие в пределах ряда определенную часть его членов. К ним относятся квартили, децили и перцентили (про-центили). Квартили — это три значения признака,

делящие ранжированный вариационный ряд на четыре равные части. Аналогично, девять децилей делят ряд на 10 равных частей, а 99 перцентилей — на 100 равных частей.

В практике используют обычно перцентили

. Причемсоответствуют первому и

третьему квартилям, между которыми находится 50% всех членов ряда, асоответствует второму квартилю и равен медиане, т. е. „Любой перцентиль определяется рядом

последовательных действий, которые можно выразить в виде следующей формулы:



где—нижняя граница класса, содержащего перцентиль; она определяется по величине, превосходящей или равнойв ряду накопленных частот. Здесь—выбранный перцентиль;—общее число наблюдений;—ширина классового интервала;—частота класса, содержащего искомый перцентиль;—так называемый порядок перцентиля, показывающий, какой процент наблюдений имеет меньшую величину, чем. Например, для Р₂₅ и Р₇₅ порядки окажутся соответственно равными 25 и 75%. Таким образом, как и при определении медианы, нахождение того или иного перцентиля связано с кумуляцией частот вариационного ряда в направлении от низшего (начального) класса к высшему.

Пример 23. Найти 50-й перцентиль ряда распределения годового удоя коров (=80), для которого определены средняя арифметическая и показатели вариации (см. пример 18, табл. 13).



Величина, она соответствует. Нижняя граница класса, содержащего, равца 2800; частота этого классаравна 20;=100. Подставляем эти величины в формулу (30):. Найденная величина оказалась очень близкой к средней арифметической годового удоя коров этой группы=2906,25 кг.

Формула (30) применима и для нахождения перцентилей безынтервальных вариационных рядов.

Пример 24. Найдите 50-й перцентиль для ряда распределения численности поросят в пометах 64 свиноматок;

В данном случае К=50*64/100=32. Эта величина больше = 24, но меньше=39. Следовательно,находится между 7-м и 8-м значениями классов, т. е.= (7+8)/2=7,5;= 15. Отсюда

Тема № 3.Выборочный метод и оценка генеральных параметров.

Цель– изучить выборочныйметод и оценку генеральных параметров.

Задачи. Генеральная совокупность и выборка. Точечные оценки. Требования, предъявляемые к точечным оценкам. Статистические ошибки.

Краткое содержание. Наблюдения над биологическими объектами могут охватывать все члены изучаемой совокупности без единого исключения или ограничиваться обследованием лишь некоторой части членов данной совокупности. В первом случае наблюдения называют полными или сплошными, во втором — частичными или выборочными. Полное обследование совокупности позволяет получать исчерпывающую информацию об изучаемом объекте, в чем и заключается преимущество этого способа перед способом выборочного наблюдения. Однако к сплошному наблюдению прибегают редко, так как эта работа сопряжена с большими затратами времени и труда, а также в силу практической невозможности или нецелесообразности проведения такой работы. Невозможно, например, учесть всех обитателей зоо- или фитопланктона даже небольшого водоема, потому что их численность практически необозрима. Нецелесообразно высевать всю партию семян для того, чтобы определить их всхожесть. В подавляющем большинстве случаев вместо сплошного наблюдения изучению подвергают некоторую часть обследуемой совокупности, по которой и судят о ее состоянии в целом.

Совокупность, из которой отбирают определенную часть ее членов для совместного изучения, называют генеральной. Отобранная тем или иным способом часть генеральной совокупности получила название выборочной совокупности или выборки. Общую сумму членов генеральной совокупности называют ее объемом и обозначают буквой N.

Теоретически объем генеральной совокупности ничем не ограничен, т. е. генеральную совокупность представляют как бесконечно большое множество относительно однородных единиц или членов, составляющих ее содержание. Практически же объем генеральной совокупности всегда ограничен и может быть различным в зависимости от объекта наблюдения и той задачи, которую приходится решать. Например, при определении продуктивности животных той или иной породы или вида генеральную совокупность составят все особи данной породы или вида. Если же вопрос о продуктивности животных решают в зоне данной области или района, то генеральную совокупность составят все животные изучаемой породы, распространенной в данной области или районе.

Объем выборки, обозначаемый буквой п, может быть и большим, и малым, но он не может содержать менее двух единиц. Выборочный метод — основной при изучении статистических совокупностей. Его преимущество перед полным учетом всех членов генеральной совокупности заключается в том, что он сокращает время и затраты труда (за счет уменьшения числа наблюдений), а главное — позволяет получать информацию

о таких групповых объектах, сплошное обследование которых практически невозможно или нецелесообразно.

Основное требование, предъявляемое к любой выборке, сводится к получению наиболее полной информации о состоянии генеральной совокупности, из которой выборка взята. Опыт показал, что правильно отобранная часть генеральной совокупности, т. е. выборка, довольно хорошо отображает структуру генеральной совокупности. Однако полного совпадения выборочных показателей с характеристиками генеральной совокупности, как правило, не бывает. Чтобы выборка наиболее полно отображала структуру генеральной совокупности, она должна быть достаточно представительной, или репрезентативной (от лат. represento — представляю). Репрезентативность выборки достигается способом рандомизации (от англ. random — случай) или случайным отбором вариант из генеральной совокупности, что обеспечивает равную возможность для всех членов генеральной совокупности попасть в состав выборки.

Существует два основных способа отбора вариант из генеральной совокупности: повторный и бесповторный. Повторный отбор производят по схеме «возвращения» учтенных единиц в генеральную совокупность, так что одна и та же единица может попасть в выборку повторно. При бесповторном отборе учтенные единицы не возвращаются в генеральную совокупность, каждая отобранная единица регистрируется только один раз. Повторный отбор не влияет на состав генеральной совокупности, и возможность каждой единицы попасть в выборку не меняется. При бесповторном отборе возможность единиц, составляющих генеральную совокупность, попасть в выборку меняется, так как каждый предшествующий отбор влияет на результаты последующего, а также и на состав генеральной совокупности, который тоже претерпевает изменения. В практике обычно применяют бесповторный случайный отбор. Так, если измеряют рост мужчин призывного возраста, то, измерив одного из них, вторично его уже не измеряют. Случайный повторный отбор служит теоретической моделью, с помощью которой изучают процессы, совершающиеся в статистических совокупностях, что имеет определенное познавательное значение.

Идеальный случайный отбор производится по методу жеребьевки или лотереи, а также с помощью таблицы случайных чисел, позволяющих полностью исключить субъективное влияние на состав выборки. Сущность этого метода заключается в следующем. На численно ограниченной, но довольно большой искусственной модели генеральной совокупности способом повторного случайного отбора образуется ряд чисел, которые заносят в таблицу таким образом, чтобы они имели одинаковое количество цифр. Этим облегчается использование такой таблицы в практических целях. Например, при трехзначности чисел цифру 8 заносят в таблицу в виде 008, а число 69 — в виде 069 и т. д. Числа записывают в таблицу в случайном порядке, поэтому ее и называют таблицей случайных чисел. Такая четырехзначная таблица помещена в Приложении (табл. IV).

Как пользоваться этой таблицей? Пусть из общего числа 120 животных, содержащихся в виварии, нужно отобрать для опыта 10 особей. Для того чтобы отбор был действительно случайным, исключающим субъективные влияния на состав выборки, необходимо поступить следующим образом. Всем животным вивария или только животным той группы, из которой намечено отобрать 10 особей, присваивают номера от 1 до п. Затем в таблице случайных чисел находят десять таких, которые не превышают п. Пусть я=120. Пользуясь табл. IV, условимся учитывать первые три цифры в каждом столбце этой таблицы (хотя можно исходить и из другого условия). В первом столбце находят числа 0905 и 0912. Согласно условию, это дает числа 90 и 91. Других нужных чисел в этом столбце нет. Во втором столбце таблицы находят числа 47 и 41. В третьем столбце обнаруживают числа 62, 84, 50 и 31. В четвертом столбце отыскивают остальные два числа: 39 и 87. Всего получилось десять чисел: 90, 91, 47, 41, 62, 84, 50, 31, 39 и 87. Особей с такими номерами включают в состав экспериментальной группы.

Наряду с простым случайным отбором в практике применяют и другие виды выборки из генеральной совокупности. К ним относится типический, серийный и механический отбор. Типический отбор используют в тех случаях, когда генеральная совокупность расчленяется на отдельные (типические) группы. Например, в хозяйстве среди крупного рогатого скота находятся первотелки, группы коров по второму, третьему и другим отелам. В таких случаях из каждой группы случайным способом отбирают одинаковое, а чаще пропорциональное число единиц. Затем вычисляют групповые характеристики, объединяемые в общую характеристику генеральной совокупности.

При серийном отборе, как и при типическом, генеральную совокупность предварительно делят на группы (серии, гнезда), образуемые обычно по территориальному принципу. Затем по усмотрению исследователя из общего количества серий или гнезд отбирают некоторое их число для совместной обработки. При этом серии могут быть как равночисленными, так и состоять из разного числа единиц. Например, из 30 групп подростков в возрасте от 14 до 15 лет намечено обследовать выборочно шесть групп. Членов этих групп и объединяют для совместного изучения. Таким образом, в отличие от типического отбора при серийной выборке из генеральной совокупности извлекают не отдельные единицы, а целые серии или гнезда относительно однородных единиц.

При механическом отборе генеральная совокупность разбивается на несколько равных частей или групп. Затем из каждой группы случайным способом отбирают по одной единице. Например, при обследовании посева ржи на урожайность намечено отобрать 100 растений (или колосьев). В таком случае поле ржи должно быть разбито на сто равных делянок. Следовательно, при механическом отборе число единиц равно численности групп, на которые разбита генеральная совокупность. Механический отбор может производиться и по другой схеме, когда в выборку попадает каждая десятая, сотая и т. п. единица генеральной совокупности. Например, при проведении ботанических или зоологических экскурсий можно регистрировать каждый пятый, десятый и т. п. экземпляр встреченных растений или животных данного вида.

Кроме типического, серийного и механического отбора в практике применяют и другие разновидности случайной выборки.

ТОЧЕЧНЫЕ ОЦЕНКИ

Числовые показатели, характеризующие генеральную совокупность, называют параметрами, а числовые показатели, характеризующие выборку,— выборочными характеристиками или статистиками. Выборочные характеристики являются приближенными оценками генеральных параметров. Это величины случайные, варьирующие вокруг своих параметров. Оценки генеральных параметров по выборочным характеристикам могут быть точечными и интервальными.

Генеральные характеристики, или параметры, принято обозначать буквами греческого

алфавита, а выборочные характеристики— латинского. Выборочная средняя х_ср является оценкой генеральной средней µ, выборочная дисперсия s_x²—оценкой генеральной дисперсии σ_х², а среднее квадратическое отклонение s_x — оценкой стандартного отклонения σ_х, характеризующего генеральную совокупность. Это точечные оценки, представляющие собой не интервалы, а числа («точки»), вычисляемые по случайной выборке.