Метода_(лабы_1-11). Механика и термодинамика

Название	Механика и термодинамика
Дата	24.11.2020
Размер	0.64 Mb.
Формат файла
Имя файла	Метода_(лабы_1-11).docx
Тип	Методические указания #153311
страница	13 из 15

1 ... 7 8 9 10 11 12 13 14 15

Работа № 10. ИССЛЕДОВАНИЕ ПРОЦЕССОВ ПЕРЕНОСА В ГАЗАХ
Цель работы:изучение явлений переноса в газе.Определение коэффи-циентов диффузии и вязкости воздуха, длины свободного пробега и эффек-тивного диаметра его молекул.
Приборы и принадлежности:прибор для измерения объемной скоро-сти истечения газа из трубки.
Исследуемые закономерности
Явления переноса. Хаотическое движение молекул в газе приводит ктому, что в объеме газа поддерживается равновесное состояние, которое ха-рактеризуется постоянством его параметров состояния и концентрации моле-кул во всем объеме.
При нарушении равновесия в газе хаотическое движение молекул при-водит к возникновению макроскопических потоков, стремящихся восстано-вить нарушенное равновесное состояние. Явления, возникающие при проте-кании этих процессов, называются явлениями переноса.
К явлениям переноса относят диффузию, внутреннее трение (вязкость), теплопроводность. В данной работе исследуются первые два явления.

Внутреннее трение это
Внутреннее трение это	z			z
				z
явление, обусловленное перено-
явление, обусловленное перено-
сом импульса молекул. Пусть при
течении газа его слои движутся
параллельно друг другу в направ-
лении оси x с различной скоро-
стью v_x(z) (рис. 10.1, а). Тогда в
стью v_x(z) (рис. 10.1, а). Тогда в			x		x
направлении, перпендикулярном		Рис. 10.1.

скорости течения газа, будет происходить перенос импульса от молекул, на-ходящихся в слоях, движущихся с большей скоростью, к молекулам, нахо-дящимся в слоях, движущихся с меньшей скоростью. Это проявляется как трение, возникающее между слоями газа. В результате скорости движения
65

слоев газа выравниваются (рис. 10.1, б). Сила трения, возникающая между слоями газа, определяется как
F_тр ^dv_dz S ,

где   коэффициент внутреннего трения (вязкости); v  скорость отдельных слоев газа; dv / dz  градиент скорости слоев газа в направлении, перпенди-кулярном к поверхности, разделяющей слои (в направлении оси z перпенди-кулярной скорости слоев v); S  площадь соприкасающихся слоев.
Течение газа в узкой цилиндрической трубке. Пусть газ течет в трубке срадиусом a и длиной l (l >> a) под действием разности давлений p на кон-цах трубки (рис. 10.2).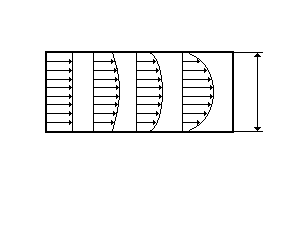

t₀ t₁ t2 t3
Рис. 10.2.
В установившемся режиме (t > t₃) из-менение скорости течения газа по сечению ²^а трубки описывается параболической зави-

симостью

		( r )  2					r	2 
v	x		v		 1				,
v			v		 1				,
				x 			a	2 
							a		

где r  расстояние, отсчитываемое от оси трубки, v_x  средняя по сечению скорость течения газа (ось x направлена по направлению скорости слоев га-

за). Вблизи стенок трубки при r = a градиент скорости равен ^dv_dr^x⁴_a^v^x.

Учитывая, что сила трения газа о стенки цилиндрической трубки
F_тр η⁴_a^v^x2πal , гдеS_б2alплощадь боковой поверхности трубки,урав-новешивает внешнюю силу, действующую на газ в трубке, F  p a² , где S _с a²–площадь сечения трубки,получим выражение для средней скоро-сти слоев газа:

 _pa²

^vx _8η_l ^.
66

Рис. 10.3.
Это выражение называется формулой Пуазейля. В данной работе изме-ряется расход газа Q  V t , определяемый как объем V газа, вытекающий из трубки за некоторый промежуток времени t. Расход газа связан со сред-ней скоростью v_x соотношением Q  pa²v_x , так что средняя скорость слоев газа по сечению трубки

_x = V / (t  a²).

Приравнивая полученные выражения для v_x , получа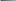ем формулу для расчета коэффициента вязкости газа:

_ πa⁴ p t _. 8l V

Диффузия  это явление, обусловленное переносом массы молекул.Ес-ли различные области занимаемого газом объема различаются концентраци-ей молекул, то в газе возникают макроскопические потоки молекул, стремя-щиеся выровнять их концентрацию. Процесс диффузии описывается законом Фика:

m  DS dρ dz ,
m  DS dρ dz ,	4

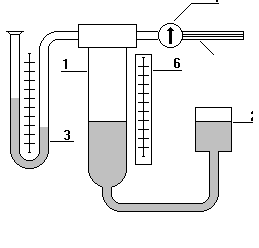где m  масса газа, переносимая через пло-

щадь поверхности S в единицу времени; D	1


 коэффициент диффузии; d/dz  градиент

плотности газа в направлении переноса		3
массы газа.

Молекулярно-кинетические соотно-шения. Кинетические коэффициенты D и
зависят от средней скорости теплового движения молекул средней длины свободного пробега   

2d ²n^¹ молекул

5

6

2

= (8RT/)^1/2 и

D ¹₃ uλ; η  ¹₃ ρuλ ;   = D.

формулах используются следующие обозначения: T  температура газа; R = 8.31 Дж/(Кмоль)  универсальная газовая постоянная;   плот-

ность газа;   его молярная масса; d  газокинетический или эффективный диаметр молекул; n – концентрация молекул газа ( n  ρN _Aμ , N _A -число Аво-гадро).
Метод измерений. Прибор для измерения объемной скорости течениягаза Q = V/t (рис. 10.3) состоит из сосуда 1 с исследуемым газом и сосуда 2,заполненного водой и присоединенного к сосуду 1 гибкой трубкой.Давле-ние в сосуде 1 регулируется перемещением по вертикали открытого сосуда 2 и измеряется U-образным манометром 3 (1 мм вод. ст.  10 Па). Сосуд 1 со-общается с атмосферой через кран 4 и узкую трубку 5. Положение уровня жидкости и изменение объема газа в сосуде 1 определяются по шкале 6.
Указания по подготовке к работе
Занесите в бланк Протокола Таблицу 10.1 для записи однократно измеряемых в опыте величин и Таблицу 10.2 по определению вязкости η воздуха.
Указания по проведению наблюдений

Запишите в Таблицу 10.1 протокола наблюдений с панели установки диа-

метр 2a и длину l капилляра, а по термометру и барометру температуру T

давление p воздуха в лаборатории.

Соедините измерительную установку

Таблица 10.1.

с атмосферой, открыв кран 4 (см. рис.

2 a, мм

l,см

t₁,C

T₁, K

p,Па

10.3). Опустите сосуд 2 в нижнее по-

ложение. Когда жидкость в обоих ко-

Таблица 10.2.

…

ленах манометра 3 установится на

p

одном уровне, закройте кран.

ⁿ0i

n_i

3. Поднимите сосуд 2 на такую высоту,

t_i

чтобы манометр 3 показывал раз-

ность давлений p  500 Па (1 мм вод. ст.  10 Па). Запишите в Таблицу 10.2 значение p и положение n₀ уровня жидкости в сосуде 1, определен-ное по шкале 6.

Откройте кран 4, одновременно включив секундомер, и, поднимая сосуд 2,поддерживайте постоянное значение разности давленийp по маномет-ру 3.

Когда объем жидкости в сосуде 1 увеличится на (5–10) см³, закройте кран и остановите секундомер. Запишите в Таблицу 10.2 конечное положение

n_lуровня жидкости в сосуде 1 и времяt течения газа по секундомеру.Разность между значениями положений уровней жидкости численно равна объему V [см³] протекающего газа (V = n_l  n₀).

Повторите измерения (пп. 2-5) 5 раз при различных значениях разности давлений p, изменяя ее с выбранным шагом 50–100 Па по указанию пре-подавателя.

Задание по обработке результатов эксперимента

Используя Таблицу 10.2, найдите вязкость воздуха η  η  η выбороч-ным методом с Р = 95%.
Учитывая, что плотность воздуха при нормальных условиях  1,29 кг/м³, вычислите методом переноса погрешностей значение коэффициента диф-фузии воздуха D  D  D с Р = 95%.

По известному из опыта значению вязкости 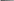η воздуха оцените среднюю длину свободного пробега λ его молекул и газокинетический диаметр d

молекул воздуха (молярная масса воздуха  = 29 ∙ 10^³ кг/моль).
4. Рассчитайте теплопроводность воздуха   c_V  , где c_V  iR / 2 – его удельная теплоемкость (i=5) и сопоставьте ее с табличным значением

 24 мВт/(м  К).

Проверьте выполнение принятых в работе допущений о стационарности течения газа и отсутствия турбулентности, т. е. завихрений при течении

69

газа. Число Рейнольдса вычисляется по формуле Re = 2a v_x /D. Для лами-нарного (гладкого, без завихрений) течения оно должно быть менее 2300. Стационарность течения газа в трубке можно проверить, рассчитав длину l_ст,на которой происходит установление стационарного распределенияскорости газа по сечению трубки, l_ст  0,1 a Re.
Контрольные вопросы

В чем сущность явлений переноса, при каких условиях они возникают?

Дайте определения коэффициента вязкости, коэффициента диффузии. Как они взаимосвязаны друг с другом? Как взаимосвязаны между собой плот-ность вещества и концентрация частиц в нем?

Сформулируйте методику измерений, используемую в лабораторной ра-боте, и опишите лабораторную установку.

Дайте определения ламинарного и турбулентного течений газа.

Каким образом определяется тип течения газа в данной работе?

Дайте определение длины свободного пробега молекул газа. Как ее можно рассчитать?

Как вычисляются средняя, среднеквадратическая и наиболее вероятная скорости молекул газа? Каков их физический (статистический) смысл?

Напишите модификации уравнения Клапейрона, выражающие давление газа через его плотность и концентрацию молекул в нем.

Азот вытекает из сосуда через горизонтальную трубку. Длина трубки l, радиус a = 0,01N (мм). Определите среднюю по сечению трубки скорость течения газа, если величина градиента давления p/l = 10k (мм рт. ст./ см). Вычислите скорость течения газа на расстоянии r = a/N от оси трубки.

Коэффициент внутреннего трения азота  = 1,710^-5 Па∙с.
10. Кислород вытекает из сосуда, где он находится под давлением p₁ = (1000 + 50N) мм рт. ст. через капилляр радиуса a = 0,01N (мм). Определите массу газа вытекающего за 1 секунду через капилляр, если наружное давление
70

составляет p₀ = 760 мм рт. ст.; температура T = 10k (⁰С); длина трубки l =

см; коэффициент внутреннего трения кислорода  = 1,910^-5 Па∙с.

Примечание. В примерах9и10,используются следующие обозначения: N –номер в группе, k – номер группы в потоке.

1 ... 7 8 9 10 11 12 13 14 15