Метода_(лабы_1-11). Механика и термодинамика

• Название: Механика и термодинамика
• Дата: 24.11.2020
• Размер: 0.64 Mb.
• Имя файла: Метода_(лабы_1-11).docx
• Тип: Методические указания; #153311
• страница: 14 из 15

Работа № 11. ИССЛЕДОВАНИЕ НЕСТАЦИОНАРНОЙ
ТЕПЛОПРОВОДНОСТИ В ДИЭЛЕКТРИЧЕСКОЙ СРЕДЕ
Цель работы:изучение закономерностей процесса тепловой диффузии

• 
  определение значения коэффициента тепловой диффузии исследуемого ма-териала.
  

Приборы и принадлежности:установка для измерения температурногополя, создаваемого в среде тепловым источником.
Исследуемые закономерности
Уравнение теплопроводности.Теплопроводность характеризует диффу-зию тепла в среде. Перенос энергии теплового движения в газах осуществля-ется через столкновения молекул, в твердых телах  посредством передачи энергии колебаний кристаллической решетки. В обоих случаях процесс пе-реноса теплоты описывается уравнением диффузии Фика:
j =  D_T grad u,
где j  плотность теплового потока; u  объемная плотность внутренней энергии среды; D_T  коэффициент тепловой диффузии. Учитывая, что объем-ная плотность внутренней энергии связана с температурой среды соотноше-нием u = cT, где с  теплоемкость единицы объема среды, можно записать уравнение теплопроводности Фурье:
j =   grad Т,
где   коэффициент теплопроводности,  = D_Tс.
Температурное поле точечного источника тепла. Рассмотрим задачуопределения температурного поля T(x; t) в однородной среде. Положим, что температурное поле создается импульсным точечным источником тепла. Рассмотрим распространение тепла вдоль однородного бесконечного стерж-ня, расположенного вдоль оси x. Начало координат совместим с положением нагревателя, который расположен перпендикулярно оси.
Пусть в тонком поперечном слое при x = 0 и t = 0 мгновенно выделилось количество теплоты Q₀. Выделившееся тепло диффундирует вдоль оси x.
71


Рис. 11.1
Распределение тепла вдоль стержня в любой момент времени соответствует нормальному закону Гаусса:

	1		exp	x2
P x				22	,
	
		2

где Р (x)  вероятность того, что к некоторому моменту времени порция теп-лоты будет иметь координату x;   среднеквадратичная ширина распределе-ния. Тогда распределение линейной плотности тепла вдоль стержня равно:

Q_ Q_{0 exp}^ ₂^x_²2 _.



x  2
Разделим обе части этого равенства на произведение (сS), где с  тепло-емкость единицы объема стержня, S  площадь его поперечного сечения:
Q1_ Q₀ 1 _exp^ ₂^x_²2 _.




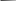
x cS  2 cS
Левая часть данного выражения есть приращение температуры относи-тельно исходной. Она равна приращению температуры T(x; t) в точке с ко-ординатой x в момент времени t по отношению к температуре в момент вре-мени t = 0:
T(x; t) = T(x; t) T(x; 0).
Тогда искомое распределе-




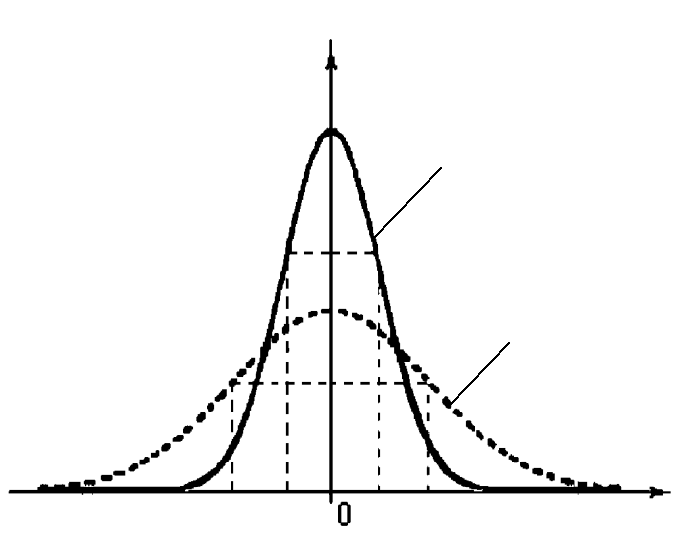
_T ние температуры вдоль стержня
имеет вид

t1		x2
	
		22 , (1)
	T ( x; t ) T ( 0;t) exp
t2	где T(0; t)  температура стержня
	к моменту времени t в точке сре-
	ды с координатой x = 0;   сред-
	неквадратичная ширина	распре-

деления температуры по коорди-

x

нате x. Кривые распределения температуры по координате для
двух моментов времени показаны на рис. 11.1.

• 
  увеличением времени параметр  увеличивается, при этом температу-ра T(0; t), соответствующая максимуму распределения, уменьшается. Нерав-
  

72

новесное состояние неравномерно нагретого стержня релаксирует к равно-весному состоянию с одинаковой температурой во всех точках стержня. За-висимость  от времени можно представить в следующем виде:

  t 		.	(2)
	2DT t
Формула (2) аналогична соотношению Смолуховского – Эйнштейна

для среднеквадратичного смещения частицы, совершающей броуновские блуждания.
Задача работы – сверить выводы теории теплопроводности в диэлек-триках с экспериментом и определить значение коэффициента тепловой диффузии для исследуемого материала.
Для этой цели зависимость (1), используя операцию логарифмирова-

ния,

можно линеаризовать и привести к виду Y  aX  b , где

Y lnT (x, t),

X  x2,
a  1/22,

b 

lnT (0,t)

.

Коэффициенты

a

и b

в этой линейной

зависимости могут быть найдены методом наименьших квадратов (МНК).

Для проверки закона  (t )  2DT t запишем его в виде
  (t )  At,	(3)

где A  2D_T . Эту формулу также можно линеаризовать, используя опера-цию логарифмирования. В результате придем к зависимости Y   X   , где Y ln, X ln t , ln A,коэффициентыив которой также могут бытьнайдены по МНК.



По найденному значению коэффициента  можно найти значение ко-эффициента A  e^ , а затем значение коэффициента тепловой диффузии,




D_T A²/ 2e^2/ 2.



Если полученное значение  близко к 1/2, то закон (t )

t в дан-



ном опыте выполняется. Степень отличия  от 1/2 может служить мерой не-выполнения теоретических допущений в данном эксперименте.




Метод измерений. В работе исследуется нестационарное распределениетемпературы в среде после кратковременного нагревания среды в некотором малом объеме. Экспериментальная установка содержит электронагреватель-ный элемент, имеющий форму пластины, и термометры, находящиеся на раз-личных расстояниях от нагревателя. Пространство между нагревателем и
73

термометрами заполнено кварцевым песком. Удельная теплоемкость песка 1.310⁶ Дж/(м³К). Геометрические размеры установки подобраны таким об-разом, что температурное поле вблизи нагревателя можно считать изменяю-щимся только вдоль одной координаты x. Направление оси x перпендикуляр-но плоскости пластины.
Указания по подготовке к работе
Занесите в бланк Протокола Таблицы 11.1 и 11.2 по определению измеряемых величин.
Таблица 11.1.

i	1	2	3	4	5	6	7
xi
						Таблица 11.2.
t, мин	T1,C	T2,C	T3,C	T4,C	T5,C	T6,C	T7,C
0
5
…

Указания по выполнению наблюдений

1. 
   Запишите координаты x_i термометров в Таблицу 11.1.
   

2. 
   Запишите начальные показания термометров T(x; 0) .
   

3. 
   Включите нагреватель, удерживая нажатой кнопку включения на панели установки в течение 5 минут.
   

4. 
   Выключите нагреватель и регистрируйте показания термометров T(x; t) через интервалы времени t = 5 мин. Количество измерений 68. Резуль-таты наблюдений занесите в Таблицу 11.2.
   

Задание по обработке результатов эксперимента

1. 
   Вычислите приращение температуры среды относительно исходной тем-пературы T(x; t) = T(x; t)  T(x; 0) для каждого момента времени t в точ-ках с координатами термометров x.
   

2. 
   Постройте графики распределения приращения температуры в координа-тах (x, T ) для каждого значения времени t _j .
   

3. Введите обозначения X i  xi2

и Yij  ln T xi ; t j . Используя МНК,

найдите по наборам экспериментальных точек ( X i , Yi1 ),

( X i , Yi2 ), ... ко-

эффициенты (

линейных зависимостей

Y1 a1 X  b1,

a1,b1), (a2,b2), ...

74

Y₂ a₂ X  b₂, ...прологарифмированного уравнения(1)для каждого мо-мента времени t _j .

4. 
   Постройте графики распределения температуры в приведенных координа-тах ( X , Y ) для каждого значения времени t _j . Для этого нанесите на коор-динатную плоскость точки ( X _i , Y_i1 ), ( X _i , Y_i2 ), ... и проведите прямые МНК Y _j  a _j X  b _j через точки ( X , Y _j ) и (0,b_j ) .
   

4. 
   Введите обозначения Y _j  ln  _j   ¹₂ ln 2 a _j , X _j ln t _j . Используя МНК, найдите по набору ( X _j , Y_j ) коэффициенты (, ) линейной зависимости Y   X  прологарифмированного уравнения(3).
   

4. 
   Сопоставьте найденное по МНК значение  со значением 1 2 и сделайте заключение о соответствии теории и эксперимента.
   
5. 
   Используя определенное по МНК значение коэффициента  , найдите зна-чение коэффициента диффузии D_T .
   

Контрольные вопросы

1. 
   При каком условии в твердом теле возникает поток тепла?
   

2. 
   Запишите уравнение теплопроводности для одномерного случая, напри-мер, распространения тепла вдоль оси x.
   

3. 
   Что означает знак «минус» в уравнении теплопроводности или диффузии?
   

4. 
   Назовите размерность следующих величин: плотность теплового потока, поток тепла.
   

5. 
   Сформулируйте методику измерений, используемую в лабораторной ра-боте, и опишите лабораторную установку.
   

6. 
   Нарисуйте распределение Гаусса и отметьте на графике среднеквадратич-ную ширину данного распределения.
   

7. 
   Поясните, почему теплопроводность твердых тел во много раз больше, чем теплопроводность газов?
   
8. 
   В каких координатах зависимость y = ae^x будет линейной?
   

9. 
   Поясните способ построения линейных зависимостей согласно МНК.
   

75