Метода_(лабы_1-11). Механика и термодинамика

• Название: Механика и термодинамика
• Дата: 24.11.2020
• Размер: 0.64 Mb.
• Имя файла: Метода_(лабы_1-11).docx
• Тип: Методические указания; #153311
• страница: 12 из 15

. Его эффективность принято характеризовать холодильным коэффициеном ,
который определяется как отношение теплоты, отнятой от охлаждаемого

газа, к затраченной в цикле работе. Для

SVT-цикла

с учетом Q12  0 и

Q23

U23



U12

 A12холодильный коэффициент

равен (обозначения

цифровых индексов согласованы с рис. 9.2).

SVT 

Q  

A



2 3



12

,

A A

A



13

12

а для nVT -цикла в предположении Q12  0

  nVT 

A12

.

A

 A

13

12

Перепишем выражения для , используя экспериментально измеряемые величины давлений, для чего значения работы А₁₂ и А_12* определим графиче-ским способом. В рV-координатах (рис. 9.2) они равны площадям трапеций, основания которых р₁ и p₂ = р_2* (либо p₃ или р_3*), а высоты  (V₂ V₁) и (V_2*V₁) соответственно. Учитывая, что p₁  p₂ и p₁  p₂  2 p₂  p₁  2 p₂ , получим

• 
   nVT ^2p2иSVT^2p2.
  

^p3^p₃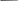

• 
  проводимом опыте p_3 > p₃, поэтому отношение холодильных коэффициентов  (nVT) /  (SVT) > 1.
  

Расчет изменения энтропии. Функция состояния,дифференциалом ко-торой является отношение Q / T, называется энтропией:

Q

2

Q

2 dT

T

dS 

,

S

  c 

 c ln

2

,

T

T

T

T

1

1

1

где c  мольная теплоемкость газа, зависящая от типа политропного процес-
са (адиабатный, изохорный, изобарный и т.п.). Отметим, что данное выраже-59


 const
ние справедливо лишь для обратимых процессов, то есть процессов, которые могут быть проведены в обратном направлении через те же промежуточные состояния, что и при прямом процессе; при этом тепловое состояние окру-жающей среды не изменяется (процесс без теплопотерь).
Выразим изменение энтропии S через экспериментально определяемые в опыте величины давлений сначала для nVT-цикла. В политропном процессе

(на участке 12) с учетом уравнения Пуассона Tp ^{(1n )/ n}

T



n 1

p



n 1



 p





n 1

p

 S   c ln

2

  c





ln

1

  c





ln



1



1



 c





1

.

12

T1

p 2



n 



n 



p 2 



n  p2

В изохорном процессе (на участке 23) изменение энтропии с учетом
T₃ T₁и i 5,а также уравнения Пуассона равно:

  c ln



n1

T3

p1

  c 

n 1



p1

 2.5 R



n 1



p1

.

S

  c

ln

n

23



V

T2

V





V 







p2 

 n

 p2



n  p2

В изотермическом процессе (на участке 31)

1

V

V



p



1

p

n

S 31  R ln

1

  R ln

1

  R ln

1



 

 R

1

.

V3

n

V2



p2 

p2

Для SVT-цикла изменение энтропии в адиабатном процессе (на участке 12^*)равно нулю.С учетом,что изменение энтропии в цикле также рано ну-
лю, заключаем, что изменения энтропии в изохорном и изотермическом про-цессах равны по величине, но различаются знаком:

S 		 R	1		p1	.
3 1			 p2

Указания по подготовке к работе
Занесите в бланк Протокола Таблицу 9.1 для записи однократно измеряемых в опыте величин и Таблицу 9.2 для определения показателя политропы.

60

Таблица 9.1.

p₂,Па V₁,л t₁,C T₁, K



Таблица 9.2.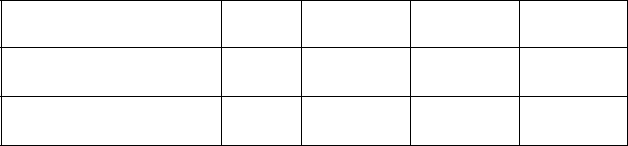



1 … … 10

p₁

p₃

Указания по проведению наблюдений

1. 
   Откройте кран на атмосферу и, когда стрелка манометра установится на нуле, закройте его.
   

2. 
   Откройте кран и, закрыв отверстие патрубка пальцем, нажмите кнопку на-соса и накачайте в баллон воздух до давления 0,8  0,9 предельного по шкале манометра, после чего закройте кран. Когда воздух в баллоне охла-
   

дится до комнатной температуры (стрелка манометра остановится), запи-шите в Таблицу 9.2 установившееся избыточное давление p₁.

3. 
   Откройте кран на атмосферу и, как только избыточное давление в баллоне упадёт до нуля, закройте кран. Когда воздух в баллоне нагреется до ком-
   

натной температуры (перестанет уменьшаться давление в баллоне), запи-шите значение установившегося избыточного давления p₃ в Таблицу 9.2 протокола.

4. 
   Действия, описанные в пп. 1, 2, выполните 10 раз.
   

5. 
   По барометру и термометру, имеющимися в лаборатории, измерьте атмосферное давление p₂ и температуру воздуха T₁. Объём баллона V₁ ука-зан на панели установки. Все измеренные величины запишите в Таблицу 9.1 протокола.
   

Задание по обработке результатов эксперимента

1. 
   Используя данные Таблицы 9.2, рассчитайте в делениях шкалы манометра
   

избыточные давления p₁  p₁   ( p₁) и p₃  p₃   ( p₃) с Р  95% .
2. Рассчитайте показатель политропы n  n  n с Р = 95% на участке 1–2 nVT цикла.При выводе формулы погрешностиnфункцию(1)удобнопрологарифмировать.

61

3. 
   Выразите избыточные давления p₁ и p₃ в Па, а комнатную температу-ру T₁ в К (одно деление шкалы манометра равно 40 Па). Рассчитайте дав-ления p₁ и p₃ , выразив их в Па.
   

3. 
   Рассчитайте параметры состояния ( p,V , T ) в точках 1, 2 и 3 nVT-цикла, а
   

также в точках 1^, 2^ и 3^ SVT-цикла, используя уравнения
политропического и адиабатического процессов. При расчётах используй-те экспериментальные значения изменения давления p₁ и p₃ и величи-ну p₂, измеренную барометром. Рассчитанные значения параметров (p,V,T)

• 
  вершинах nVT- и SVT- циклов сведите в две отдельные таблицы.
  

3. 
   Постройте nVT- и SVT-циклы в координатах (р, V) на миллиметровой бу-маге в удобном масштабе.
   

3. 
   Рассчитайте изменения внутренней энергии, величину работы газа и поглощаемое (отдаваемое) им количество теплоты для всех процессов nVT цикла. Для участка 1-2 используйте при расчетах определенное в опыте значение мольной теплоемкости воздуха в политропном процессе. Проверьте выполнение первого начала термодинамики для каждой из ветвей цикла и всего цикла.
   

3. 
   Рассчитайте холодильные коэффициенты для nVT- и SVT-циклов. Сравни-те значения холодильных коэффициентов, полученные расчетным путем, с холодильными коэффициентами обратимого цикла Карно, построенного
   

• 
  пределах тех же максимальных и минимальных температур циклов, т. е.
  

Т₁, Т₂и Т₂^*соответственно.Обратите внимание,что холодильные коэффи-циенты обратимых циклов Карно меньше, чем холодильные коэффициен-ты рассматриваемых циклов.

8. 
   Используя уравнения состояния идеального газа, найдите число молей воздуха в сосуде  по известным значениям p₂, V₁, T₁ в Таблице 9.1. Счи-тается, что число молей газа при его сжатии и расширении в исследуемом цикле – постоянная величина.
   

62

9. 
   Рассчитайте мольную теплоемкость c_V воздуха при постоянном объеме, а по формуле (2) – его мольную теплоёмкость c в политропном процессе.
   
10. 
    Рассчитайте изменение энтропии всех процессов в nVT- и SVT-циклах.
    

Контрольные вопросы

1. 
   Какой газ называют идеальным?
   

2. 
   Дайте определение степеней свободы молекул газа (поступательных, вращательных и колебательных). Как рассчитываются полные степени свободы молекул газа и чему они равны при невысоких температурах для одноатомного, двухатомного и многоатомного газов? Рассчитайте (с уче-
   

том колебательных степеней свободы) полное число степеней свободы молекул O₂ и CO₂ .

3. 
   Какие циклы называют тепловыми, а какие холодильными? Какими па-раметрами принято характеризовать эффективность этих циклов?
   

4. 
   Что такое состояние вещества? Какие величины называют параметрами состояния? Напишите уравнение состояния идеального газа.
   

5. 
   Дайте определение термодинамических функций: работы газа A, его внутренней энергии U, количества теплоты Q, отдаваемой (получаемой) газом, энтропии S . Какие из этих функций являются функциями состояния, а какие функциями процесса? Чему равно изменение функций состояния в цикле?
   

6. 
   Какие процессы называют политропными? Дайте определение показателя политропы. Чему равны показатели политропы для изохорного, изобарного, изотермического и адиабатного процессов?
   

7. 
   Как экспериментально определяется показатель политропы в данной ра-боте? Докажите формулу, по которой он рассчитывается.
   

8. 
   Сформулируйте объединенный газовый закон, и, исходя из него, напиши-те уравнения изохоры, изобары и изотермы.
   

63

9. 
   Сформулируйте первое начало термодинамики. Какой вид оно имеет для каждой из ветвей цикла, а также всего цикла? Напишите первое начало для изобарного, изохорного, изотермического и адиабатного процессов.
   

9. 
   Дайте определение удельной и мольной теплоемкостей вещества. Как они взаимосвязаны друг с другом? Каковы их размерности?
   

9. 
   Как можно вычислить теплоемкость идеального газа в произвольном по-литропном процессе через показатель политропы? Докажите эту форму-лу.
   

9. 
   Объясните, почему теплоемкость воздуха в политропном процессе в дан-ной работе отрицательна?
   

9. 
   Напишите уравнение Пуассона в переменных (p,V), (p,T) и (V,T).
   

9. 
   Дайте определение холодильного коэффициента. Как он вычисляется в цикле, изучаемом в данной работе?
   

9. 
   Как соотносятся холодильные коэффициенты nVT- и SVT- циклов? Ка-
   

кой из них больше и почему?

16. 
    Покажите, что холодильный коэффициент (ХК)  холодильника и КПД  тепловой машины, работающих по взаимно обратным циклам, связаны соотношением   1  1.
    

16. 
    В каких интервалах изменяются ХК  и КПД  ? Может ли тепловая
    

машина с высоким КПД, если ее цикл обратить, работать как хороший холодильник, и наоборот?

18. 
    Дайте термодинамическое и статистическое (формула Больцмана) опре-деление энтропии. Как можно вычислить ее изменение в произвольном политропном процессе?
    

18. 
    Какие формулировки второго начала термодинамики вам известны? Дай-те энтропийную формулировку второго начала.
    

64