Метода_(лабы_1-11). Механика и термодинамика

• Название: Механика и термодинамика
• Дата: 24.11.2020
• Размер: 0.64 Mb.
• Имя файла: Метода_(лабы_1-11).docx
• Тип: Методические указания; #153311
• страница: 8 из 15

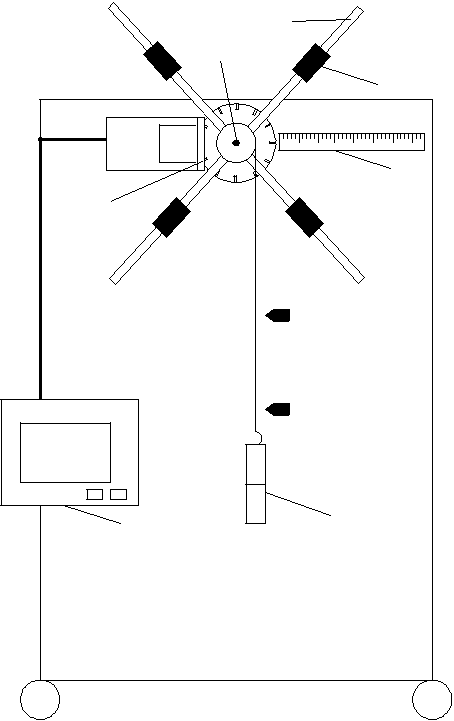
Работа №7. МАЯТНИК ОБЕРБЕКА
Цель работы. Экспериментальное исследование законов динамикивращательного движения твердого тела на примере маятника Обербека, оп-ределение постоянной части момента инерции маятника Обербека.
Приборы и принадлежности.
Маятник Обербека (рис. 7.1) представляет собой крестовину 1 с груза-ми 2, на вращающейся оси 3. На шкив на оси намотана нить с грузиком 5, ко-торая, разматываясь, вызывает вращательное движение крестовины. На че-тырех взаимно перпендикулярных стержнях крестовины располагаются че-тыре подвижных груза 2 массой т каждый, положение которых относитель-но оси вращения маятника определяется по измерительной линейке 6. В опы-
те положения грузов на крестовине меняют с помощью их перемещения по 40

резьбовым спицам крестовины. Фиксация грузов в каждой серии измерений осуществ-ляется путем законтривания двух резьбовых половин каждого груза в выбранном поло-жении. На оси крестовины располагается датчик 4 угловой скорости вращения маят-ника, подключенный через концентратор к измерительному блоку 7.
Исследуемые закономерности
Вращение маятника описывается ос-новным уравнением динамики вращательно-го движения

	1
	3
	2
	6
4
7	5
	Рис. 7.1.

M  I ε ,

(1)

где М – момент сил, действующих на маятник, I – его момент инерции. Вращательный момент М сил, действующих на маятник, определяется
выражением:
M  TR  M_тр, (2)
где Т – сила, действующая на шкив маятника со стороны нити, M _тр – момент
сил трения в оси маятника, R – радиус шкива, на который намотана нить с
прикрепленным к ней грузом m₀ .
Движение груза m₀ на нити описывается вторым законом Ньютона

m0 a  m0 g T .	(3)
С учетом этого уравнения момент сил, действующих на маятник, мож-
но записать в виде:
M  m0(g  a)R  Mтр .	(4)

Если подставить (4) в (1), то уравнение вращательного движения маят-ника примет вид
Iε m₀g  a R  M _тр.
41

С учетом, что угловое ускорение ε вращения маятника связано с ускорением

а движения грузаm0соотношением
a εR ,	(5)
это уравнение можно привести к виду:
I  m0 R 2ε m0 gR  M тр .	(6)

В этой формуле правая часть равенства есть постоянная величина. От-сюда следует, что вращение маятника для выбранного в опыте положения грузов является равноускоренным. Кроме того, из формулы (6) следует, что
увеличение момента инерции I системы должно приводить в данной работе к уменьшению углового ускорения ε ее вращения, и наоборот.
Если m – масса одного из грузов на крестовине, r – его расстояние до оси вращения маятника, то момент инерции крестовины с 4-мя грузами в формуле (6) равен

		I  I 04I m m r 2 I C4m r 2 ,				(7)
где I	0	– суммарный момент инерции крестовины без грузов,	I	m	 mr2	- мо-

мент инерции одного из подвижных грузов, рассчитанный по теореме Гюй-генса-Штейнера, I_m его собственный момент инерции, I _C  I ₀  4I_m – посто-янная часть момента инерции маятника Обербека.

Момент инерции I_C в данной работе является экспериментально опре-деляемой величиной. Для его нахождения запишем (6) для двух различных

положений r_i и r_j грузов m относительно оси вращения маятника:

I C	 4m ri			2	 m0 R 2εi	 m0 gR  M тр,	(8)
I C	 4m r j2				 m0 R 2εj	 m0 gR  M тр .	(9)
Равенство правых частей этих равенств означает и равенство их левых
частей:
I C4m ri			2 m0 R 2εi I C4m r j2 m0 R2εj				(10)

Отсюда можно найти искомую величину I_C :
42

 4m

r 2ε

j

 r 2ε

i

 m R2

I

j

i

,

(11)

C

ε i

 ε j

0

где i  j , и при ri  rj должно быть  i

  j . В этой формуле величины

r ²ε  r ²ε

I C, R , m, m0–константы,поэтому множительbi j j j i i constпри раз-ε _i  ε _j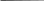



личной геометрии постановки эксперимента.
Для выполнения работы необходимо выполнить три серии измерений угловых ускорений ε₁ , ε₂ и ε₃ маятника при трех различных удаленностях r₁, r₂и r₃грузов на крестовине от оси ее вращения.

Угловое ускорение вращения маятника определяется по формуле

• 
   2  / t ²  2 h / Rt ² , где   h / R – угол поворота шкива при прохождении
  

грузом на нити расстояния h между двумя метками на установке за время t. Операцию определения времени t и вычисления ε в работе выполняет изме-рительный блок установки. При этом средние значения t и ε по четырем из-мерениям в одном опыте высвечиваются на ЖК дисплее установки.
Указания по подготовке к работе
Занесите в протокол Таблицу 7.1 для записи параметров установки и Таблицу 7.2 для записи результатов наблюдений.

Таблица 7.1.

m,г

m0,г

R,см

l,см

h,см

r1,см

r2,см

r3,см

Таблица 7.2.

r1,см

t1,с

1, м с2

r2,см

t 2,с

2, м с2

r3,см

t 3,с

3, м с2

Указания по проведению наблюдений

1. 
   Запишите в Таблицу 7.1 массы грузов m  53 г на крестовине маятника и на нити шкива m₀ 119 г , радиус шкива R =16.5 мм, высоту (длину) гру-зов на крестовине l  24 мм , расстояние между метками на установке h =
   

43

430 мм и удаленности грузов на крестовине от ее оси вращения
r212см, r316см. Приборные погрешности масс 2 г , θ R
r18см,
 0.5 мм,

θ l
 θ h
 θ r
1 мм .

2. 
   Соберите лабораторную установку, зафиксировав подвижные грузы на вы-бранном расстоянии r₁ от оси вращения маятника. ВНИМАНИЕ! При ус-
   

тановке грузов на крестовине отметка на линейке, соответствующая их выбранному положению, должна быть видна сквозь зазор между грузами, т.е. совпадать с положением их общего центра масс.