Метода_(лабы_1-11). Механика и термодинамика

• Название: Механика и термодинамика
• Дата: 24.11.2020
• Размер: 0.64 Mb.
• Имя файла: Метода_(лабы_1-11).docx
• Тип: Методические указания; #153311
• страница: 5 из 15

Работа № 4. ПРОВЕРКА ТЕОРЕМЫ ГЮЙГЕНСА – ШТЕЙНЕРА МЕТОДОМ ВРАЩАТЕЛЬНЫХ КОЛЕБАНИЙ
Цель работы. Определение момента инерции эталонного диска мето-дом вращательных колебаний и экспериментальная проверка теоремы Гюй-генса-Штейнера.
3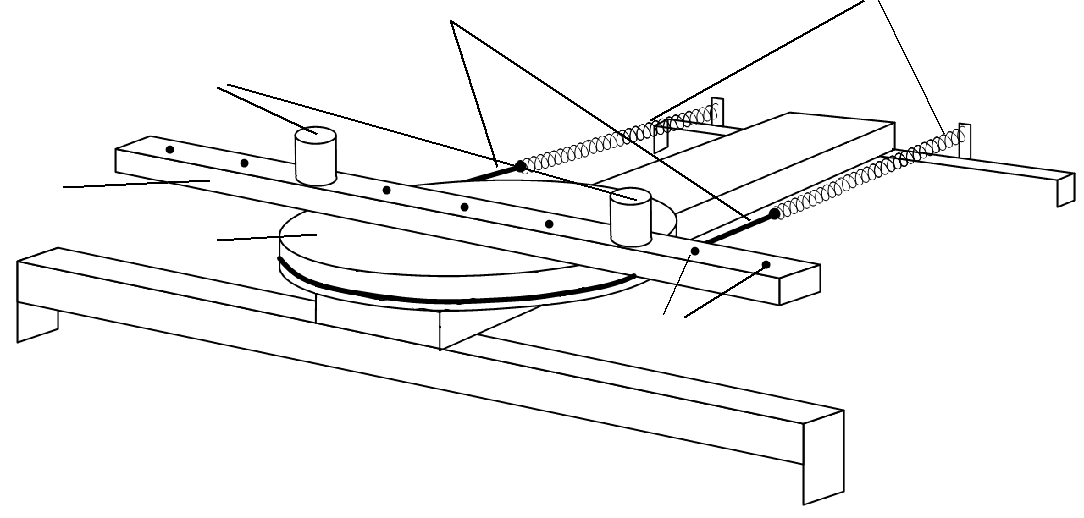




2
6


4
1

5

Рис. 4.1.
Приборы и принадлежности. Лабораторная установка(рис.4.1)вклю-чает колебательную систему, вращающуюся в горизонтальной плоскости, ко-
25

торая состоит из закрепленного на вертикальной оси диска (шкива) 1, ремень 2 которого связан с упругими пружинами 3, зацепленными за штыри стойки.

• 
  шкиву жестко прикреплен металлический профиль 4 с рядом отверстий 5, в которых фиксируются грузы 6.
  

Исследуемые закономерности
Период колебаний T подвижной части колебательной системы, исполь-
зуемой в работе, связан с ее моментом инерции I. Выведем эту зависимость.

• 
  положении равновесия силы упругости пружин, а, следовательно, и силы
  

натяжения нити с разных сторон диска (шкива) одинаковы. Обозначим эти силы F₀. Для выведения шкива из положения равновесия повернем его на угол . По закону Гука силы упругости изменятся на kd/2, здесь k – коэф-
фициент жесткости системы последовательно соединенных пружин d – диа-
метр шкива. Тогда натяжение одной пружины увеличится, а другой умень-шится на kd 2 , и на шкив будет действовать возвращающий момент сил:

M 

d

 F  k

d







d

 F  k

d

 

 

d

2

k

(1)





0

2



0

2



2

2 



2 



Подставляя (1) в основное уравнение динамики вращательного движе-

ния

M I.

(2)

и учитывая, что   , получаем дифференциальное уравнение для :

I  

d 2

k 0,  2 0,

2

которое имеет вид дифференциального уравнения гармонического осцилля-тора. Из теории дифференциальных уравнений известно, что его решение имеет вид:

  ₀ cos(t  ) .
Здесь ₀ и  – константы, определяемые начальными условиями, а

 	d 2k	(3)
	2I

– собственная частота колебаний рассматриваемого маятника. 26

Если обозначить I ₀ , ₀ , T₀ соответственно момент инерции, частоту и период системы, в которой грузы 6 (рис. 4.1) помещены на металлическом профиле 4 в центр шкива 1, то согласно формуле (3):

I0	d 2k		d 2 kТ0	2	(4)
	2  2		82
	0

Если грузы переместить симметрично относительно оси вращения сис-темы вдоль металлического профиля на шкиве в положения (1-1), (2-2) и т.д., то момент инерции I , частота  и период T колебательной системы изме-нятся, и ее момент инерции станет равным:

I 	d 2 k			d 2 kТ 2
				(5)
	22
			82

Из (4), (5) видно, что отношение моментов инерции равно:

I			2		T		2
	 	0		 			 .		(6)
I 0		
				 T0		

Если радиус цилиндров R , а их масса m , то при установке цилиндров на расстоянии r от оси вращения колебательной системы ее момент инерции равен

IIД2



1

mR

2

 mr

2



 I 0

 2mr

2





(7)

2





где I Д момент инерции диска 1 с металлическим профилем 4,

1

mR 2

 m r 2–

2

момент инерции одного цилиндра, рассчитанный согласно теореме Гюйген-са-Штейнера, I ₀  I _Д  mR² – постоянная часть момента инерции колеба-тельной системы.

С учетом формул (6), (7) выражение для I₀ имеет вид:

I0		2mr		2	(8)
		2
		T		1
			
	T0 

Формула (8) получена при использовании теоремы Гюйгенса-Штейнера, а значит, хотя и косвенным образом, может быть использована для проверки правильности этой теоремы. Для этого достаточно убедиться,
27

что значения моментов инерции I₀ , определенные при разных положениях цилиндров относительно оси вращения колебательной системы примерно одинаковы.
Если момент инерции I₀ определен, то из формулы (4) можно найти жесткость колебательной системы в данном эксперименте:

k 	8π2 I0	.	(9)
	2 2
	d Т0

Указания по подготовке к работе
Создайте Таблицы 4.1 и 4.2 для занесения параметров установки и ре-зультатов наблюдений.

Таблица 4.1

№	0	1	2	3	4	
r,см	0	6.0	10.0	14.0	18.0	0.2
t , с

Таблица 4.2

m,г	d,мм	R,мм
2002	1382	162

Указания по проведению наблюдений

1. 
   Осторожно обращайтесь с подвижной системой. Не допускайте чрез-мерного растяжения пружин – это может привести к потере их упругих свойств.
   

2. 
   Установите цилиндры в центре диска (позиция (0-0)). Отклоните указа-
   

тель диска на угол примерно 30 и измерьте время n = 5 его колебаний с помощью любого датчика времени, имеющего точность θ _t  0, 01 с. Ре-зультат наблюдения занесите в Таблицу 4.1. Опыт повторите N = 5 раз.

3. 
   Устанавливая цилиндры симметрично относительно оси вращения сис-темы в положениях (1-1), (2-2), (3-3), (4-4) на металлическом профиле диска, повторите опыт п. 2 для этих положений цилиндров. Результаты измерений занесите в Таблицу 4.1.
   

Задание по обработке результатов эксперимента

1. 
   Рассчитайте параметры t_i , T_i  t_i / n, I_0i . Сопоставьте значения моментов инерции колебательной системы I_0i и сделайте заключение о справедли-вости теоремы Гюйгенса-Штейнера.
   

28

2. 
   Рассчитайте постоянную часть момента инерции колебательной системы
   

I ₀ I ₀ I ₀ с Р 95%.

2. 
   Используя значения моментов инерции I₀ и двух цилиндров m R² , рас-считайте момент инерции I _Д диска (шкива).
   

2. 
   Используя формулу (9), рассчитайте жесткость колебательной системы k  k   k с Р 95%.Погрешностьk рассчитайте по формуле,выве-денной в подготовке к работе.
   

Контрольные вопросы

1. 
   Что такое жесткость колебательной системы и каков ее физический смысл? Как экспериментально ее можно определить?
   

2. 
   Дайте определение момента силы, момента импульса и момента инер-ции абсолютно твердого тела относительно некоторой оси.
   

3. 
   Сформулируйте теорему Гюйгенса–Штейнера, которая используется для вычисления момента инерции тела относительно произвольной оси вра-щения.
   

4. 
   Сформулируйте основной закон динамики вращательного движения. Каков физический смысл входящих в него параметров?
   

5. 
   Сформулируйте методику измерений, используемую в лабораторной ра-боте, и опишите лабораторную установку.
   

6. 
   Напишите дифференциальные уравнения гармонических колебаний с затуханием и без затухания и их решения. Каков смысл входящих в них параметров?
   

7. 
   Докажите, что функция (t )  ₀ cos(t  ) является решением диффе-
   

ренциального уравнения   ²  0 .

8. 
   Выведите формулу (8) для расчета постоянной части момента инерции колебательной системы в данной работе.
   

8. 
   Выведите формулу расчета приборной погрешности θ_{I 0i} постоянной
   

части момента инерции колебательной системы.

10. 
    Выведите формулу (9) для расчета жесткости колебательной системы в данной работе.
    

10. 
    Рассчитайте момент инерции тела по указанию преподавателя.
    

29