Метода_(лабы_1-11). Механика и термодинамика

• Название: Механика и термодинамика
• Дата: 24.11.2020
• Размер: 0.64 Mb.
• Имя файла: Метода_(лабы_1-11).docx
• Тип: Методические указания; #153311
• страница: 2 из 15

водная скорости по нормали к слоям, S – площадь соприкосновения слоев, 
– коэффициент внутреннего трения (динамическая вязкость). Величина об-ратная вязкости 1  называется текучестью. Наряду с динамической вязко-
стью часто используется кинематическая вязкость    , где  – плотность жидкости.
Внутреннее трение в газах определяется переносом импульса при пе-реходе молекул из одного слоя газа в другой. На движение молекул в жидко-сти, в отличие от газа, сильно влияет межмолекулярное взаимодействие, ог-раничивающее их подвижность. Молекула жидкости большую часть времени совершает колебания около положения равновесия внутри небольшого объе-ма. Поэтому во внутреннее трение в жидкости дополнительный вклад дает взаимодействие между молекулами слоев жидкости. Как следствие, вязкость жидкостей в очень сильной степени зависит от температуры. С ростом тем-пературы подвижность молекул жидкости возрастает, а вязкость падает, т.к. с увеличением температуры тепловое движение молекул усиливается, а сред-нее время “оседлой жизни” молекулы (время релаксации) уменьшается. При невысоких температурах коэффициент динамической вязкости изменяется по закону   C expE kT ,где k –постоянная Больцмана,T–абсолютная тем-
пература, E – энергия, которую должна приобрести молекула, чтобы перейти от од-ного положения к другому (энергия актива-ции). Характерный вид температурной за-висимости вязкости изображен на рис. 1.3.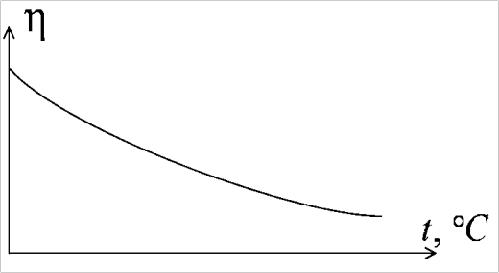




Сила сопротивления движению тела в вязкой среде. В вязкой среде на движу-
6
щееся тело действует сила сопротивления, направленная противоположно скорости тела. При небольших скоростях и небольших размерах тела эта сила обусловлена вязким трением между слоями среды и пропорциональна скоро-сти тела

F_r rv,
где v – скорость движения тела, r – коэффициент сопротивления, зависящий от формы, размеров тела и от вязкости среды .
Для шара радиуса R коэффициент сопротивления определяется форму-лой Стокса

18. 
     6R .
    

При движении тела в вязкой среде происходит рассеяние (диссипация) его кинетической энергии. Слои жидкости, находящиеся на разном расстоя-нии от движущегося тела, имеют различную скорость. Слой жидкости, нахо-дящийся в непосредственной близости от поверхности движущегося тела, имеет ту же скорость, что и тело, по мере удаления от него скорость слоев жидкости плавно уменьшается, рис. 1.4. В этом состоит явление вязкого тре-ния, в результате которого движения тела передается слоям окружающей среды в направлении, перпендикулярном движению тела. Если скорость тела

велика или тело имеет большие размеры, за те-
лом возникают вихри и обтекание становится
турбулентным. В этом случае сила сопротивле-
ния становится	пропорциональной квадрату
скорости: F  kSρ		v2 , где S – площадь по-
r		ж 2	v
перечного сечения тела, а ρж – плотность жид-
			Рис.2.
кости, k – коэффициент пропорциональности.			Рис. 1.4.

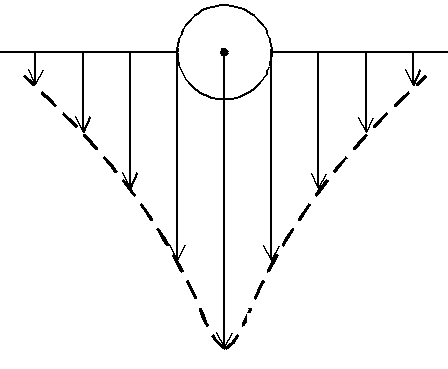Сила сопротивления при турбулентном обтекании определяется не столько трением одних слоев жидкости о другие, сколько увеличением кинетической энергии жидкости, вынужденной двигаться, чтобы расступиться и пропус-тить тело.
Критерием характера движения слоев жидкости (ламинарного или тур-булентного) при падении в ней шарика радиуса R со скоростью v является


7

число Рейнольдса Re  2ρ_ж vR / . При Re<2300 движение слоев – лами-нарное, при Re 2300 – турбулентное.
Движение тела в диссипативной среде. Рассмотрим падение шарика вжидкости. В исследуемом в лабораторной работе случае скорость падения шарика невелика, и можно считать, что сила сопротивления пропорциональ-на первой степени его скорости. Пусть начальная скорость шарика у поверх-ности жидкости v₀ , его радиус R , а ρ_ж и ρ_т – плотности жидкости и шарика соответственно. Согласно II закону Ньютона:

• 
  m  mv mg  F_А F_r F  r v.
  

Здесь F_A – сила Архимеда, F_r – сила Стокса, F  mg  F_А

• 
  m(1 _ж _т )g – движущая сила, m – присоединенная масса жидкости, ув-
  

лекаемая телом за собой. Присоединенной массой называется такая фиктив-ная масса жидкости, кинетическая энергия которой при ее движении со ско-ростью тела равна кинетической энергии окружающей тело жидкости. При-соединенная масса зависит от размеров и формы погруженной в жидкость части тела. Для шарика присоединенная масса равна половине массы вытес-

ненной

жидкости:



3

3

 mж/ 2т

,

откуда

m  жV 22ж R

m  m  m(2т ж) / 2т,

m/ m  ж/ 2т.

Если

ввести

обозначения

 

r



9η

,

 

F

 2g

ρ т  ρж

, то задача

сведется к

m  m

R2

2 т  ж 

m  m

2ρт  ж

решению неоднородного дифференциального уравнения вида v   v   .

Данное уравнение имеет решение

v (t) v v v0

et,

a (t )

d v

 a0 et,

dt

где v₀ – скорость падения шарика на поверхность жидкости или его началь-

ная скорость, v_  ^_ 
шарика, a₀   ( v_  v₀ )
^{2gR2  т  ж } – установившаяся скорость движения




9

• 
  2 g ^{ρ т  ρж } 1  ^{v0 } – его начальное ускорение.
  

2ρ_т  _ж ^_v_^_

8

Зависимость скорости движения
тела в диссипативной среде от времени	v0			v
представлена на рис. 1.5. Видно, что
скорость шарика в зависимости от ве-					v0 v
личины начальной скорости может ли-
бо убывать, при v0   , либо возрас-	v					V0
	
тать при 0  v0    , но в любом слу-					v0 v
чае асимптотически стремится к по-						t	
стоянному значению v .
	0			1	2	3	4
Время, за которое величина ус-					Рисис.1.4.5..
корения a по отношению к своему на-

чальному значению a₀ изменяется в e раз или отклонение скорости тела от равновесной скорости v  v_ по отношению к своему начальному значению v₀ v_изменяется вeраз называется временем релаксации процесса пере-хода движения тела от нестационарного режима к стационарному. Его также
можно найти как   ¹  ^{v  v0} . В исследуемом случае характерное значе- a₀



ние  составляет доли секунды. Время движения шарика до первой метки многократно превышает  , и движение шарика между метками можно счи-тать равномерным, а значение его установившейся скорости находить как v_l t ,где l расстояние между метками.
Второй закон Ньютона в случае стационарного движения шарика имеет вид mg  F_А  F_r  0 или

		ρ	ж	
r v mg 1				
		ρт 

Из полученного уравнения может быть найден коэффициент сопротив-ления среды:

r 	mg 				ж 			,
			 1				
	v				
		 				т 

• 
  по формуле Стокса–Эйнштейна – вязкость среды:
  
  • 
    _ ^r _ ^{mg } _{1 } ^ρж ^ _. 6π R 6π Rv_ ^_ ρ_т ^_
    

9
Радиус шарика может быть выражен через его массу m  (4 3)πR³ρ_т .
Тогда

η  A	m2/3
		,	(1)
	v

где А – константа, зависящая от плотности жидкости и материала шарика:

A 	g		4πρ	т	1/3			ρ	ж	
						 1				 .
			3
	6π 							ρт 

В лабораторной работе в качестве жидкости используется глицерино-вое масло, его плотность _ж 1.1 г см³ , материал шарика – свинец, _св 11.3 г см³ или сталь _ст  7.8 г см³ .

Превращение энергии в диссипативной системе.
Полная механическая энергия движущегося в жидкости тела в произ-вольный момент времени определяется выражением

		 ж				2	(t)
W (t ) mgh 1					( m  m ) v			,
		т 			2

где h – высота расположения тела над дном сосуда. В установившемся режи-ме

							v	2
W (t ) mgh 1		ж							.
	т 					2

Передача энергии жидкой среде, окружающей движущееся тело, про-исходит за счет совершения работы против сил трения. Энергия при этом превращается в тепло. Скорость диссипации энергии (мощность потерь) в ус-тановившемся режиме может быть найдена как

P  			dW (t)	 F v rv2.
d		dt		r 		
Уравнение баланса энергии на участке установившегося движения
имеет вид:
	Fl  P t ,			или mg	 1 		ρс	l  r v2 t ,		(3)
		d							
							ρт 

10

где l  v_t – путь, проходимый телом между двумя метками, за время t. Уравнения движения тела (второй закон Ньютона) и баланса энергии при ус-тановившемся движении тела эквивалентны друг другу.
Указания по подготовке к работе
Занесите в протокол Таблицу 1.1 для записи результатов наблюдений и Таблицу 1.2 для записи постоянных и однократно измеряемых в опыте вели-чин.

Таблица 1.1

Таблица 1.2

1

2

3

4

5



ρ ж , г см3

ρ т , г см3

l,см

h0,см

t,C

m ,мг

t ,с

Указания по проведению наблюдений

1. 
   На аналитических весах взвесьте поочередно пять шариков. После взве-
   

шивания каждый шарик заверните в лист бумаги и напишите на ней массу шарика. Массы шариков m и приборную погрешность весов _m занесите в Таблицу 1.1 протокола наблюдений.

2. 
   Поочередно опуская шарики в жидкость через впускной патрубок, из-мерьте секундомером время t прохождения каждым шариком расстояния между двумя метками на боковой поверхности сосуда. Результаты изме-рений и приборную погрешность секундомера занесите в Таблицу 1.1 протокола.
   

3. 
   Измерьте миллиметровой линейкой и занесите в Таблицу 1.2 протокола расстояние l между метками на сосуде и расстояние h₀ от верхней по-верхности патрубка до поверхности жидкости, а также температуру t, C воздуха в лаборатории и значения плотностей жидкости и материала ша-
   

риков  _ж и _т .
Задание по обработке результатов эксперимента

1. 
   Рассчитайте значение коэффициента A в формуле вязкости (1).
   

2. 
   По данным Таблицы 1.1 результатов наблюдений определите значения установившейся скорости v_  l t для каждого из опытов и вязкости жид-
   

кости      c P  95 % выборочным методом.


11

3. 
   Для одного из опытов рассчитайте коэффициент сопротивления r и мощ-ность рассеяния P_d , а также проверьте баланс энергии на участке устано-
   

вившегося движения (3).

4. 
   Для одного из опытов рассчитайте число Рейнольдса и сделайте вывод о характере движения слоев жидкости относительно друг друга при падении шарика в ней.
   

4. 
   Для одного из опытов рассчитайте начальные скорость v₀  2gh₀ , уско-
   

рение a₀ и время релаксации   ( v_  v₀ ) / a₀ . Постройте графики зави-симостей v  v(t) и a  a(t) на миллиметровой бумаге.

6. 
   Вычислите количество теплоты, выделяющееся за счет трения шарика о жидкость, при его прохождении между двумя метками.
   

6. 
   Сравните экспериментальное значение вязкости с табличным (см. раздел Справочные материалы).
   

Контрольные вопросы

1. 
   Какие параметры характеризуют исследуемую систему как диссипатив-ную? От каких величин зависит коэффициент сопротивления движению тела в диссипативной среде?
   

2. 
   Дайте определения динамической, кинематической вязкости и текучести жидкости.
   

3. 
   Объясните характер температурной зависимости вязкости жидкостей и га-зов.
   

4. 
   В чем отличие ламинарного течения от турбулентного? Как величина чис-ла Рейнольдса характеризует вид течения жидкости при падении шарика в ней.
   

5. 
   Объясните методику измерения вязкости, использованную в лабораторной работе.
   

6. 
   Как зависит сила сопротивления движению шарика в жидкости от скоро-сти при малых и больших скоростях его движения?
   

7. 
   Чем обусловлена необходимость учета присоединенной массы?
   

8. 
   Как вычислить количество теплоты, выделяющееся за счет трения шарика о жидкость, при его прохождении между двумя метками.
   

12

9. 
   Сделайте рисунок и укажите на нем все силы, действующие на шарик, па-дающий в жидкости. Используя обозначения сил, указанных на рисунке, напишите уравнение движения шарика (второй закон Ньютона) в дисси-пативной среде в нестационарном и стационарном режимах его движения.
   

9. 
   Выразите все силы, действующие на шарик, через радиус шарика и, под-
   

ставив их во второй закон Ньютона в стационарном режиме, найдите вы-ражение для вязкости жидкости через радиус шарика.
11. Получите выражение для коэффициента А в формуле вязкости жидкости.

12. 
    Используя метод логарифмирования функции, выведите формулу при-борной погрешности вязкости жидкости _.
    

12. 
    Обоснуйте, почему в данной работе для обработки данных косвенных из-мерений нельзя применять метод переноса погрешностей, но возможно применение выборочного метода.
    

12. 
    Как называются величины a₀ , v₀ , v_,  и как они взаимосвязаны друг с
    

другом?



 

0



t



0



15. Докажите что функция v(t )  v

 v

 v

e

a ( t )v(t )

t

яв-

a e

ляется решением дифференциального

уравнения

v   v  ,

где

 /   v , a0  ( v  v0 ) .