Метода_(лабы_1-11). Механика и термодинамика

• Название: Механика и термодинамика
• Дата: 24.11.2020
• Размер: 0.64 Mb.
• Имя файла: Метода_(лабы_1-11).docx
• Тип: Методические указания; #153311
• страница: 4 из 15

Работа № 3. ИССЛЕДОВАНИЕ ДИНАМИКИ КОЛЕБАТЕЛЬНОГО И ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
Цель работы:исследование динамики колебательного движения напримере крутильного маятника, определение момента инерции маятника, модуля сдвига материала его подвеса и характеристик колебательной систе-мы с затуханием (логарифмического декремента затухания и добротности колебательной системы).

	Приборы и принадлежности:крутильный
	маятник, секундомер, масштабная линейка, мик-
	рометр.
	Применяемый в работе крутильный маятник
	(рис. 3.1) представляет собой диск 1, закреплен-
	ный на упругой стальной проволоке 2, свободный
	конец которой зажат в неподвижном кронштейне
	3. На кронштейне расположено кольцо 4, масса ко-
	торого известна. Кольцо 4 можно положить сверху
Рис. 3.1.	на диск 1, изменив тем самым момент инерции ма-
	ятника. Для отсчета значений угла поворота маят-

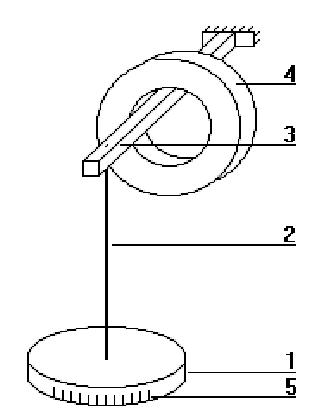ника служит градуированная шкала 5, помещенная на панели прибора снизу от диска 1.
Исследуемые закономерности
Момент инерции крутильного маятника
Момент инерции (аналог инертной массы тела при его поступательном движении) – физическая величина, характеризующая инертные свойства твердого тела при его вращении. В соответствии с одной из формулировок основного уравнения динамики вращательного движения
M  I ε ,
где момент инерции I связывает угловое ускорение тела  и момент сил M, действующих на него.
18


Рис. 3.2.
Если твердое тело вращается вокруг неподвижной оси, то момент инерции относительно этой оси вычисляется как сумма произведений эле-ментарных масс m_i, составляющих тело, на квадраты их расстояний r_i до оси вращения, т.е.

9. 
      m_i r_i²V_i r_i²,
   

i i
где  – плотность тела, V_i – элементы объема. Таким образом, момент инерции является аддитивной величиной.

• 
  случае сплошного тела сумма в определении момента инерции пере-ходит в интеграл:
  

I  r ² dm r ²dV .

m V
Крутильный маятник совершает вращательное колебательное движение вокруг оси, совпадающей с направлением стальной проволоки. Используя
основное уравнение динамики враща-тельного движения, можно определить момент инерции маятника, а также фи-зические величины, описывающие вращательное движение.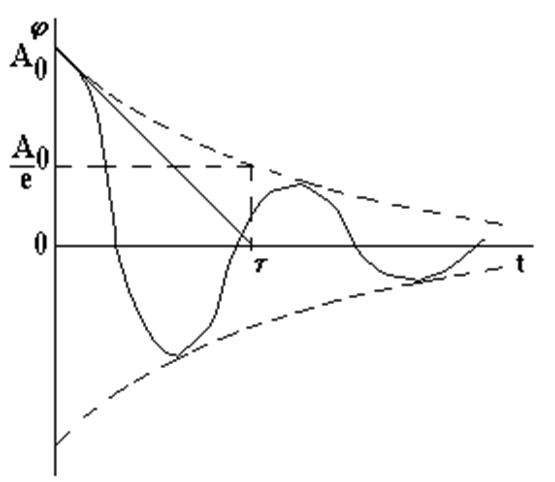



Уравнение движения крутильно-го маятника. При повороте тела,за-крепленного на упругом подвесе, в ре-зультате деформации сдвига возникает вращающий момент упругих сил M   k ,гдеk–коэффициент круче-
ния, зависящий от упругих свойств материала подвеса, его размеров и фор-мы,  - угол поворота диска маятника. Без учета сил трения в подвесе урав-нение движения тела имеет вид

I	d 2	  k или	20	,
	dt 2		0

которое является уравнением гармонического осциллятора с частотой собст-венных колебаний ₀  k I , I –момент инерции диска крутильного маят-ника.




19

Трение в подвесе создает тормозящий момент, пропорциональный ско-рости движения маятника, M _R   R d  dt   R,где R –коэффициент со-противления. С учетом сил трения уравнение движения маятника принимает вид

I	d 2	  R	d	 k ,или	d 2	 2	d	20,
	dt 2		dt		dt 2		dt	0

• 
  котором коэффициент  = R/2I называют коэффициентом затухания. По-следнее уравнение является уравнением гармонического осциллятора с зату-
  

ханием. Решение этого уравнения при ₀²   ²  0 описывает затухающие ко-лебания маятника и имеет вид (при условии, что диск повернут относительно положения равновесия и отпущен без толчка)

	t
	 cos t ,		(1)
(t )  A(t ) cos  t  A e
0

где A₀ – начальная амплитуда колебаний маятника, измеряемая в радианах,

• 
   1  – время затухания колебаний, определяющее скорость убывания ам-
  

плитуды A(t) колебаний маятника, численно равное времени, за которое ам-плитуда колебаний убывает в e раз A( )  A₀ e (рис.3.2),–частота колеба-
ний осциллятора с затуханием, связанная с собственной частотой соотноше-
нием   ₀²  1 ² . Время затухания колебаний  выражается через момент инерции I и коэффициент сопротивления R материала подвеса маятника




1 2I R.
Исследуемый в работе крутильный маятник представляет собой слож-ную систему (диск с различными креплениями, прикрепленный к проволоч-ному подвесу) с неизвестным моментом инерции I_д , который представляет
собой постоянную часть исследуемой системы. Если на диск маятника поло-жить тело с известным моментом инерции  кольцо с моментом инерции I_к , то момент инерции маятника станет равным I_д  I_к . Коэффициент кручения

материала

подвеса

маятника

при

этом

не

изменяется:

k  2 I

д

 2

( I

д

 I

к

)  const , где



и



 собственные частоты кру-

0д

0к

0д

0к

тильных колебаний «диска» маятника без кольца и с кольцом. Отсюда можно найти неизвестный момент инерции диска маятника
20

Iд		Iк					(2)
			2
		0д		1
		
		0к	

где	I к		m	Dex2 Din2–момент инерции кольца,Dex,Din			– внешний и внут-
		8
ренний диаметры кольца, m – его масса.
	Крутильный маятник как диссипативная система
	Полная энергия колебаний маятника убывает со временем по закону
					2t
					 ,		(3)
				W (t ) W e
		0
где	W  kA 22–начальная энергия колебаний.Убывание энергии происхо-
	0	0

дит за счет совершения работы против сил трения. Энергия при этом пре-вращается в тепло. Скорость диссипации энергии (мощность потерь) может быть найдена как:

P  	dW		2W (t)	.	(4)
d	dt		

Помимо коэффициента затухания  (или времени затухания ) и мощ-ности потерь P_d колебательная диссипативная система характеризуется также добротностью Q, позволяющей судить о способности системы сохранять энергию. Добротность определяется отношением запасенной системой энер-гии к потерям энергии за время T 2   1 , что соответствует изменению фа-зы колебания на 1 радиан. Из этого определения следует, что

Q2	W			 			 Ne,	(5)
	Pd T		2		T

т. е. добротность численно равна числу колебаний за время t   . За это время амплитуда колебаний уменьшается в e^23 раза, а энергия колебаний

• 
  e^2535раз,иными словами за это время колебания практически затухают.Часто также используется параметр N _e  τ / T – число колебаний, за которое
  

амплитуда колебаний уменьшается в e раз.

• 
  технике для характеристики колебательных систем с затуханием вво-дят декремент затухания , равный отношению амплитуд колебаний, отли-
  

21

Рис. 3.3.

чающихся на период колебаний, мент затухания  = ln.
и его логарифм – логарифмический декре-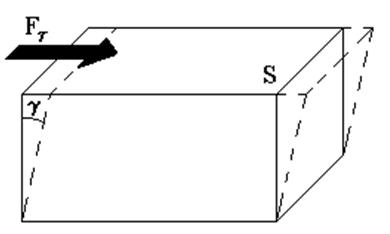

 



откуда
=T

A(t)	 eT
A(t  T )

• 
  ¹  ^π . N _e Q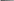
  

Определение модуля сдвига. Методом крутильных колебаний
пользуются для косвенного измерения модуля сдвига G материала подвеса. Модуль сдвига характеризует упругие свойства материала и в случае малых деформаций равен силе, действующей на единицу площади S при единичном угле сдвига  (рис. 3.3) касательно сдвигу слоев вещества в месте определе-ния модуля G.
Для подвеса из стальной проволоки модуль сдвига определяется из со-отношения

G 	32kl	,	(6)
	d 4
где l – длина подвеса, d – его диаметр,	k –его коэффициент кручения.
Модуль сдвига G связан с модулем Юнга, характеризующим сопро-
тивление материала сжатию или растяжению, соотношением			E 2G1 .

Коэффициент Пуассона    _  – отношение поперечной и продольной относительной деформации образца материала и для металлов близок к 0.3.



Указания по подготовке к работе
Занесите в протокол Таблицу 3.1 для записи результатов наблюдений времени десяти полных колебаний диска без кольца и с кольцом и времен уменьшения амплитуды колебаний маятника в два раза, а также Таблицу 3.2 для записи параметров установки и однократно измеряемых в опыте величин.

Таблица 3.1

№ t_д, с t_0д, с t_к, с t_0к, с



1
…

Таблица 3.2
l d D_ex D_in D₀ h₀ m ^ρ

22

Указания по выполнению наблюдений

1. 
   Измерить или записать с панели установки в Таблицу 2 протокола наблю-дений длину подвеса l, диаметр проволоки подвеса d, а также внешний D_ex
   

• 
  внутренний D_in диаметры кольца, диаметр D₀ и толщину h₀ диска маят-ника, а также значения массы m и плотности ρ материала диска маятника
  

• 
  кольца.
  

2. 
   Снять, если это необходимо, кольцо с диска и укрепить его на кронштей-не. Измерить время t_д n 10 полных колебаний маятника без кольца, для
   

чего повернуть диск на некоторый угол (примерно 30^о) и отпустить его, включив одновременно секундомер с точностью измерения времени _t  0.01c . Отсчитав n = 10 полных колебаний, отключить секундомер. Измерения повторить 5 раз, занося результаты измерений t_д в Таблицу 3.1 протокола наблюдений.

3. 
   Повернуть диск, отклонив указатель диска маятника на 8 или 6: делений,
   

и, отпустив диск и включив одновременно секундомер, измерить время t_0думеньшения амплитуды колебаний маятника в2раза(до4или3деле-ний). Измерения повторить 5 раз, занося результаты измерений t_0д в Таб-лицу 3.1 протокола наблюдений.

4. 
   Положить кольцо на диск и повторить 5 раз измерения времен t_к и t_0к для диска с кольцом, аналогичные пп. 2 и 3. Результаты измерений занести в Таблицу 3.1 протокола наблюдений.
   

Задание по обработке результатов эксперимента

1. Определить

по данным Таблицы 3.1 значения времен tд 

tд tд,

tк

t0д

tк tк,

t0д t0д,t0кt0к t0кс Р =95%.

2. 
   Рассчитайте периоды (T  t n)колебаний диска без кольца и с кольцом
   

T_д T_д T_д,T_кT_к T_кс Р 95%.

2. 
   Рассчитайте времена затухания (   t₀ / ln 2) колебаний диска без кольца и
   

с кольцом _д  _д  _д , _к  _к  _к с Р  95% . Время затухания коле-баний вычисляется по формуле (если установка настроена, то a₀ =0 и a₁/ a_t2)
23

 		t0
	ln	a1	 a0
		at	 a0.

4. 
   Рассчитайте собственные частоты колебаний маятника без кольца и с
   

кольцом _{0 д}  _{0 д}  _0д , _{0 к}  _{0 к}  _{0 к} с Р  95% .

5. 
   Используя данные Таблицы 3.2 протокола наблюдений, рассчитайте мо-мент инерции кольца I_к в формуле (2).
   

5. 
   Рассчитать момент инерции диска I _д  I _д  I _д с Р  95% . Для вывода
   

формулы погрешности I_д удобно формулу (2) записать в виде

		I	к	2
I				0к	и прологарифмировать это выражение.
		 2		 2
	д
		0д		0к

7. 
   Используя данные Таблицы 3.2, рассчитайте значение момента инерции диска маятника I_д , исходя из его размеров и плотности материала. Срав-нить полученный результат с экспериментальным значением в п. 6.
   
8. 
   Найдите коэффициент кручения k  ω₀²_д I_д и, используя данные Таблицы
   

2, по формуле (6) – значение модуля сдвига G и модуля Юнга E материа-ла подвеса маятника.

9. 
   Пользуясь формулами (3)–(5), определите начальное значение полной энергии W₀ , мощности потерь P_d и добротности маятника Q .
   

10. В соответствии с уравнением затухающих колебаний (1) постройте для маятника без кольца графики зависимости угла поворота маятника

• 
   (t) и амплитуды A  A(t) его колебаний от времени t.
  

Контрольные вопросы

1. 
   Сформулируйте основное уравнение динамики вращательного движения.
   

2. 
   Дайте определение момента инерции. В чем состоит его физический смысл?
   

3. 
   Какие параметры характеризуют исследуемую систему как диссипатив-ную?
   

4. 
   Дайте определение времени затухания колебаний.
   

5. 
   Сформулируйте методику измерений, используемую в лабораторной ра-боте, и опишите лабораторную установку.
   

24

6. 
   Дайте определение модуля сдвига. В чем состоит физический смысл этой величины?
   

6. 
   Напишите дифференциальные уравнения движения гармонического ос-циллятора без затухания и с затуханием, а также решения этих уравнений. Объясните физический смысл величин, входящих в эти уравнения.
   

6. 
   Выведите формулы для моментов инерции кольца I_к и маятника без кольца I_д в пп. 5 и 6 Задания по обработке результатов эксперимента.
   

6. 
   Дайте определение времени затухания колебаний. Как определить время затухания, пользуясь графиком переходного процесса (зависимости ам-плитуды колебаний маятника от времени) в диссипативной системе?
   

10. Дайте определения добротности колебательной системы и логарифмиче-ского декремента затухания. Как они взаимосвязаны друг с другом? Каков физический смысл этих параметров? Исходя из определений этих пара-метров, выведите формулы для их расчета.