Метода_(лабы_1-11). Механика и термодинамика

• Название: Механика и термодинамика
• Дата: 24.11.2020
• Размер: 0.64 Mb.
• Имя файла: Метода_(лабы_1-11).docx
• Тип: Методические указания; #153311
• страница: 3 из 15

Работа № 2. ИССЛЕДОВАНИЕ ДИНАМИКИ СВОБОДНЫХ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ В ПОЛЕ СИЛЫ ТЯЖЕСТИ

Цель работы: изучение закономерностей колеба-тельного движения тела в однородном поле силы тяжести; исследование процессов превращения энергии в консерва-тивных системах; определение момента инерции физиче-ского маятника.
Приборы и принадлежности: физический маятник;секундомер; масштабная линейка, чертежный треуголь-ник.
Конструкция оборотного маятника представлена на рис. 2.1. На стержне 1 закреплены два диска – D₁ и D₂. Ма-ятник может быть подвешен на кронштейне к легкой призме, трение в которой пренебрежимо мало.
13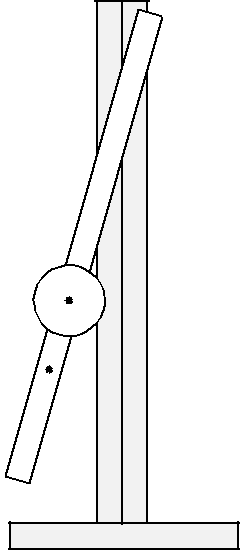


P0




D₂
D₁

Рис. 2.1

Исследуемые закономерности
Физический маятник – это тело с распределенной массой или система тел, ось вращения которого расположена выше центра масс маятника. Отно-сительно этой оси маятник колеблется с периодом

T 2

I

 2

l0

(1)

0

mgxc

g

где для составного маятника m  mi  масса маятника,

xc

1

mi xci



m

положение его центра масс относительно оси вращения, mi

и xci

 масса

i-

го тела и положение его центра масс относительно оси вращения,

I Ii



полный момент инерции маятника,

I

i

 I

0i

 m x2

– момент инерции i-го те-

i

ci

ла, рассчитанный относительно оси вращения

по теореме Штейнера, I0i



момент инерции этого тела относительно его центра масс. Длина математи-ческого маятника, период которого совпадает с периодом колебаний данного физического маятника называется приведенной длиной физического маятни-ка. Ее можно найти как l₀  I / mx_c  gT₀² / 4² . Ее можно определить экспе-риментально, если найти новую ось O , называемую осью качания, относи-тельно которой маятник колеблется с тем же периодом T₀ , что и относитель-но оси вращения O . Расстояние между осями вращения и качания OO  l₀ и будет приведенной длиной физического маятника.
Полный момент инерции маятника может быть представлен в виде:

						I  I	0	 mx2		(2)
									c
где I 0  I0i ,					1	mi xci2средний квадрат положений центров масс
	xc2
					m

системы тел, составляющих маятник.
Если период колебаний маятника определен экспериментально, то из
(1) можно найти момент инерции маятника:

I  mgx T 2	/42.	(3)
c 0

Сохранение энергии гармонических колебаний.Поскольку физический
маятник, качающийся под действием силы тяжести, является консервативной
14

системой, можно проанализировать процесс перехода потенциальной энер-гии маятника в кинетическую и обратно.
Потенциальная энергия при достижении амплитудного значения угла отклонения маятника равна:

W	 mgh  mgx (1cos		m	)  2 mgx sin2	m		1	mgx 2	(4)
pm	c	c		c	2		2	c m

где h_c  высота поднятия центра масс маятника при его максимальном от-клонении от положения равновесия, x_c – положение центра масс маятника относительно его точки подвеса, _m  максимальный угол отклонения маят-ника от положения равновесия.
При малых углах отклонения маятника (до 20°) максимальная потенци-альная энергия равна:
W_pm¹₂ mgx_c_m².



Максимальная кинетическая энергия физического маятника

	I2		mgx T 22
W 	m		c 0 m	,	(5)
km	2		82

где момент инерции маятника выражен по формуле (3) через период его ко-лебаний. Из закона сохранения полной механической энергии

23. 
     W_k+W _p=W_kmW_pm= const
    

можно найти максимальную угловую скорость маятника при прохождении им положения равновесия _m  2 _m / T₀ .
Указания по подготовке к работе
Занесите в протокол таблицу 2.1 для записи результатов наблюдений времени десяти полных колебаний маятника. Занесите в протокол таблицу 2.2 для записи однократно измеряемых в опыте величин.

Таблица 2.1

1 2 … 5 



t ,с


Таблица 2.2

l d D₁ D₂ h₁h₂ m ^ρ x_c x₁ x₂ x₃

Указания по проведению наблюдений

1. 
   Убедитесь, что стержень маятника параллелен вертикальной стойке кронштейна. Если это не соблюдается, выровняйте основание маятника.
   

15

2. 
   Запишите в Таблицу 2.2 протокола наблюдений с панели установки массу маятника m, длину l и диаметр d стержня, диаметры D₁ , D₂ и толщины h₁, h₂дисков,плотность материалρ,из которого изготовлены элементымаятника.
   

2. 
   Подвесьте маятник за призму P₀ (см. рис 2.1). Измерьте относительно вершины призмы P₀ положения центров масс x₁ , x₂ дисков и середины x₃ стержня. Результаты измерений запишите в Таблицу 2.2.
   

2. 
   Положите маятник на круглый карандаш или на ребро чертежной линей-ки, имеющей форму треугольной призмы, и найдите положение x_c центра
   

масс маятника (точку его равновесия). Его положение относительно вер-шины призмы P₀ запишите в Таблицу 2.2.

2. 
   Подвесьте оборотный маятник на призме P₀. Отклоните маятник на угол, составляющий примерно 5° – это соответствует совпадению образующей верхнего диска маятника с вертикальной кромкой линейки кронштейна. С помощью чертежного треугольника и линейки шкалы на стойке крон-
   

штейна определите (однократно) катеты треугольника для угла отклоне-ния маятника  _m  tg_m . Отпустите маятник и измерьте с помощью се-кундомера время, за которое маятник совершает n = 10 полных колебаний. Запишите время колебаний t в Таблицу 2.1 протокола наблюдений. По-вторите эти измерения 5 раз.

2. 
   Запишите приборную погрешность измерения времени в протокол.
   

Задание по обработке результатов эксперимента
1. Рассчитайте по Таблице 2.1 протокола время n 10 колебаний маятника t  t   t c P 95%.

2. 
   Рассчитайте период T  t / n колебаний маятника T₀  T₀  T₀ с P  95% .
   

3. Рассчитайте

по

формуле

(3)

момент

инерции

маятника

I 

 

c P  95% относительно оси подвеса.

I

I

4. 
   Используя измеренные значения параметров x_c и _m в пп. 4 и 5 указаний
   

по выполнению наблюдений, рассчитайте по формуле (4) полную механи-ческую энергию маятника W  W_pm .

4. 
   Рассчитайте приведенную длину маятника l₀  I / mx_c  gT₀² / 4² .
   

16

6. 
   Используя данные Таблицы 2.2 протокола, рассчитайте массы m₁ , m₂ дис-ков маятника и его стержня m₃ . Для проверки правильности расчетов со-поставьте сумму этих масс m  m_i с полной массой маятника m в Таб-лице 2.
   

6. 
   Используя п. 6 и данные Таблицы 2.2 протокола наблюдений, рассчитайте положение центра масс маятника x_c и сопоставьте его со значением опре-деленным экспериментально и занесенным в Таблицу 2.2.
   

6. 
   Используя данные Таблицы 2.2 и п. 6 данного раздела, рассчитайте по
   

теореме Штейнера моменты инерции каждого из тел составного маятника и его полный момент инерции I  I_i . Сопоставьте его значение с опре-
деленным экспериментально в п. 3.
Контрольные вопросы

1. 
   Какие колебания называют гармоническими? Объясните смысл требова-ния малости угловой амплитуды колебаний маятника.
   

2. 
   Какой маятник называют физическим, а какой математическим? Что такое приведенная длина физического маятника? Как ее определить экспери-ментально?
   

3. 
   Дайте определение центра масс системы тел.
   

4. 
   Дайте определение моментов инерции материальной точки и составного тела.
   

5. 
   Сформулируйте методику измерений, используемую в лабораторной ра-боте, и опишите лабораторную установку.
   

6. 
   Сформулируйте теорему Штейнера.
   

7. 
   Одинаковы или различны угловые и линейные ускорения и скорости раз-личных точек маятника в фиксированный момент времени при его коле-баниях.
   

8. 
   Какие законы используются для описания колебаний физического маят-ника?
   

9. 
   Напишите дифференциальное уравнение гармонических колебаний ос-циллятора и его решение и объясните физический смысл величин, входя-щих в это уравнение.
   

17

10. Покажите, что максимальные кинетическая и потенциальная энергии тела, колеблющегося по гармоническому закону, совпадают с его полной меха-нической энергией.