Метода_(лабы_1-11). Механика и термодинамика

• Название: Механика и термодинамика
• Дата: 24.11.2020
• Размер: 0.64 Mb.
• Имя файла: Метода_(лабы_1-11).docx
• Тип: Методические указания; #153311
• страница: 7 из 15

Работа № 6. ИССЛЕДОВАНИЕ ДИНАМИКИ ПОСТУПАТЕЛЬНО-ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
Цель работы:изучение законов поступательно-вращательного движе-ния твердого тела, сохранения энергии, определение момента инерции маят-ника.
Приборы и принадлежности:маятник Максвелла,секундомер,мас-штабная линейка, штангенциркуль.
Маятник Максвелла (рис. 6.1) представляет собой диск 6, закреп-ленный на стержне 7, подвешенном на бифилярном подвесе 5 к верхнему кронштейну 2. На диск крепится кольцо 8. Верхний кронштейн 2, ус-тановленный на вертикальной стойке 1, имеет электромагнит и устройство 4 для регулировки длины бифилярного подвеса. Маятник с кольцом фиксируется в верхнем исходном положении с помощью электромагнита.

34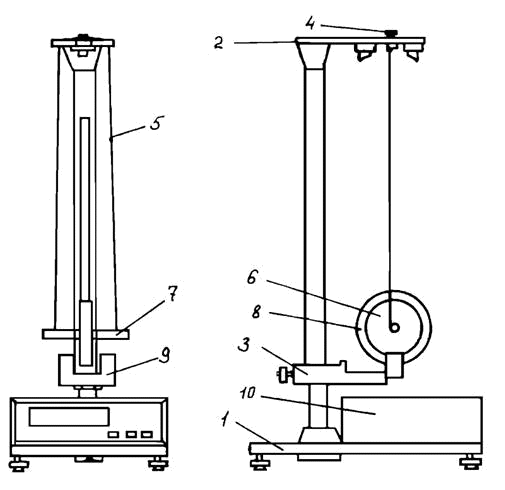

На вертикальной стойке 1 на-несена миллиметровая шкала, по ко-торой определяется ход маятника. На нижнем кронштейне 3 находится фотоэлектрический датчик 9. Крон-штейн обеспечивает возможность перемещения фотодатчика вдоль вертикальной стойки и его фиксиро-вания в любом положении в преде-лах шкалы 0…420 мм. Фотодатчик

Рис. 6.1.

предназначен для выдачи электриче-
ских сигналов на секундомер 10 в момент пересечения светового луча оси фотодатчика диском маятника.
Исследуемые закономерности
Маятник Максвелла массой m, поднятый на высоту h путем намотки нитей подвеса на стержень маятника, имеет потенциальную энергию mgh. После отключения электромагнита маятник начинает раскручиваться, совер-шая поступательно-вращательное движение. Потенциальная энергия маятни-ка переходит в кинетическую энергию поступательного движения mv² 2 его центра масс и энергию вращательного движения I ² 2 вокруг него. На уча-стках опускания и подъема маятника потери энергии на трение пренебрежи-мо малы по сравнению с изменением механической энергии. В момент пол-ного разматывания нити происходит рывок маятника и частичный переход механической энергии в тепло. На основании закона сохранения механиче-ской энергии на участке пути, меньшем длины нити, можно написать

mgh 

mv 2



I 2



mv 2





I



,

(1)

 1



2

2

2

mr

2





где v  ωr – скорость маятника в момент пересечения оптической оси фото-
датчика; ω – его угловая скорость вращения в тот же момент времени, r – 35

радиус стержня, на который намотана нить бифилярного подвеса маятника, I
– момент инерции маятника. Из уравнения (1) получим для эксперименталь-
ного значения момента инерции маятника

2

 2gh



2



g  a 

I  mr



 1 

 mr





(2)

v

2







a 

где учтено, что v ²  2ah , a – ускорение, с которым опускается маятник. Учи-тывая, что a  2 h / t ² , получим

	2	 gt 2		
I  mr				1.	(3)
			2h
				
				

Если учитывать теплоту Q , выделяющуюся маятником в момент рывка нити, то закон сохранения энергии после рывка нити будет иметь вид

mgh₀₁ mgh₀₂ mv ²/ 2 J ²/ 2 Q ,
где высоты h₀₁ и h₀₂ отсчитываются в системе координат, ось высот которой направлена вверх, а начало находится в точке рывка нити.

Из этого уравнения следует, что количество теплоты, выделяющееся при рывке, можно оценить по изменению высоты первого подъёма маятника: Q = mgh,гдеh –изменение высоты наивысшего положения маятника впервом цикле спуск – подъем.
Теоретическое значение момента инерции маятника относительно его оси рассчитывается по формуле

I	т		1	( m	r 2 M ( r 2 R 2) m ( R 2	 R2)),	(4)
			2	ст	к	0

где m_ст – масса стержня; M – масса диска, укрепленного на стержне; m_к – масса кольца; r – радиус стержня, R – внешний радиус диска; R₀ – внешний радиус кольца.
Указания по подготовке к работе
Создайте Таблицы 6.1 и 6.2 для занесения параметров установки и ре-зультатов наблюдений.
36

Таблица 6.1

mст,	M ,	mк,	r,	R,	R0,	h0,	h1,	h2,
г	г	г	мм	мм	мм	см	см	см
29	131

Таблица 6.2

i h_0i,см t₁,с … t₅,с




1
…
4

Указания по проведению наблюдений

1. 
   Измерьте штангенциркулем диаметры стержня d, диска D и кольца D₀ и рассчитайте их радиусы r  d 2 , R  D 2 , R₀  D₀ 2 . Занесите их, а также массу кольца m_к (указана на его боковой поверхности) в Таблицу 6.1 про-токола. Некоторые из этих параметров могут быть указаны на панели ус-тановки.
   

2. 
   Опустите вниз диск маятника. Произведите регулировку положения осно-вания установки при помощи регулировочных опор так, чтобы бифиляр-ный подвес маятника шел параллельно вертикальной стойке установки, а диск находился посередине оси фотодатчика. Установите с помощью уст-ройства 4 максимальную длину бифилярного подвеса, меньшую его пол-ной длины, таким образом, чтобы нижний край кольца маятника находил-
   

ся на 45 мм ниже оптической оси фотодатчика; при этом ось маятника должна занять горизонтальное положение. Запишите положение h_0i опти-ческой оси фотодатчика по шкале миллиметровой линейки в Таблицу 6.2.

3. 
   Нажмите кнопку «СЕТЬ», расположенную на лицевой панели секундоме-ра; при этом должны загореться лампочки фотодатчика и цифровые инди-каторы секундомера. Вращая маятник, зафиксируйте его в верхнем поло-жении при помощи электромагнита; при этом необходимо следить за тем,
   

чтобы нить наматывалась на стержень виток к витку. Запишите положе-ние h₀ нижнего края кольца маятника по миллиметровой шкале на верти-кальной стойке установки в Таблицу 6.1.

4. 
   Нажмите кнопку «СБРОС», затем кнопку «ПУСК». При этом электромаг-нит обесточивается, маятник раскручивается, секундомер начинает произ-водить отсчет времени, прекращающийся в момент пересечения маятни-
   

37

ком оптической оси фотодатчика. Запишите значение времени t_i в Табли-цу 6.2. Вращая маятник, вновь зафиксируйте его в верхнем положении. Нажав последовательно кнопки «СБРОС» и «ПУСК», повторите наблю-дения еще 4 раза для данной высоты свободного хода маятника. Результа-ты наблюдений занесите в Таблицу 6.2.

5. 
   Установите новую длину свободного хода маятника. Для этого поднимите нижний кронштейн с фотодатчиком на 56 см и зафиксируйте его на
   

стойке. С помощью винта 4 вновь установите необходимую длину бифи-лярного подвеса и запишите новое положение h_0i оси фотодатчика в Таб-лицу 6.2. Проведите 5 наблюдений по определению времени t_i свободно-го хода маятника для новой высоты.

5. 
   Указанную в п. 3 процедуру проделайте еще для двух высот, уменьшая каждый раз длину свободного хода на 56 см. Таким образом, для четырех высот свободного хода маятника будет получено 20 значений времени и четыре средних значений времен движения маятника для этих высот.
   

5. 
   Опустите кронштейн с фотодатчиком в крайнее нижнее положение. Отре-гулируйте бифилярный подвес для свободного хода маятника в соответст-
   

вии с п. 2. Поднимите маятник в верхнее положение и нажмите кнопку ПУСК. Определите высоту h₂ , на которую поднимется ось маятника по-сле рывка нити, и запишите ее в Таблицу 6.1 протокола.
Задание по обработке результатов эксперимента

1. 
   Рассчитайте среднее значение ускорения падения маятника и его полную погрешность a  a  a с Р = 95 %.
   

2. 
   Рассчитайте по формуле (2). момент инерции маятника I  I  I с Р = 95 %. Формулу погрешности I выведите методом логарифмирования функции.
   

3. 
   Для одного из опытов рассчитайте по формуле (3) величину момента инерции I маятника.
   

38

4. 
   Рассчитайте по формуле (4) теоретическое значение момента инерции ма-ятника I_т и сопоставьте его со средним экспериментальным значением I
   

в п. 2 и рассчитанным в п. 3. Сделайте заключение о причинах расхожде-ния значений моментов инерции, если таковое имеется.

5. 
   Рассчитайте количество теплоты Q, выделяющейся при рывке нити маят-
   

ника в нижней точке его движения. При расчете h  h2  h1 используйте
значения начальной высоты оси маятника h1   ( R0  h0 ) и высоты ее подъема после рывка h₂ . Высоты h₁ и h₂ отсчитываются по шкале изме-рительной линейки на вертикальной стойке установки, положительное на-правление оси высот которой направлено вниз.
Контрольные вопросы

1. 
   Сформулируйте методику измерений, используемую в лабораторной работе, и опишите лабораторную установку.
   

2. 
   Объясните, на каком участке движения и почему возможно применение закона сохранения механической энергии для описания движения маятни-ка.
   

3. 
   Докажите уравнения связи между линейными и угловыми величинами при
   

вращательном движении тела s  φ r , v  ωr , a	τ	 εr , a  ω2r . Каков
		n

смысл входящих в эти выражения параметров? Одинаковы ли значения величин φ,ω,ε относительно параллельных осей вращения в фиксирован-ный момент времени?

4. 
   Используя одну из высот и время падения с нее маятника в данной работе, рассчитайте
   

а) линейное a и угловое ε ускорение маятника,
б) линейную v и угловую ω скорость маятника, а также частоту n его вращения в этот момент времени,
г) угол поворота  и число оборотов N, которое сделает маятник за это время.
39

5. 
   Сделайте упрощенный рисунок маятника, используемого в данной работе,
   

и укажите на нем все силы, действующие на него. Используя рисунок, на-пишите второй закон Ньютона для центра масс маятника и уравнение вращательного движения маятника вокруг него. Из этой системы уравне-ний найдите выражение для ускорения падения маятника.

6. 
   Какая из сил на рисунке в п. 3 играет роль силы трения качения? Чему равна работа этой силы, если проскальзывание между нитью и стержнем отсутствует?
   

6. 
   Рассчитайте величину силы натяжения нити маятника.
   

6. 
   Напишите закон сохранения механической энергии для маятника в данной лабораторной работе и получите из него выражение для ускорения его па-дения.
   
7. 
   Используя теоретическое значение момента инерции маятника I_т , рассчи-тайте ускорение a падения маятника и сопоставьте его с эксперименталь-ным средним значением, полученным в данной работе.
   

6. 
   Каким образом можно оценить количество теплоты, выделяющееся при рывке нити маятника в данной работе?