Метода_(лабы_1-11). Механика и термодинамика

• Название: Механика и термодинамика
• Дата: 24.11.2020
• Размер: 0.64 Mb.
• Имя файла: Метода_(лабы_1-11).docx
• Тип: Методические указания; #153311
• страница: 10 из 15

, Гц

A_


51

Указания по проведению наблюдений

1. 
   Включите генератор звуковых колебаний и установите на нем частоту,
   

указанную на панели установки ( ₀ 1000 Гц ). Запишите установленное значение частоты и ее приборную погрешность _ в Таблицу 8.1.

2. 
   Включите осциллограф, и после появления на экране сигнала (синусоиды)
   

установите удобный для наблюдения размер изображения (амплитуды сиг-нала). Для этого, перемещая поршень в резонаторе, убедитесь, что макси-мальная амплитуда синусоиды, высвечиваемой на экране осциллографа, не выходит за пределы экрана и не слишком мала.

3. 
   Поршень с микрофоном придвиньте к телефону. Медленно удаляя микрофон от телефона, найдите положение, при котором на экране осцил-
   

лографа наблюдается первый максимум амплитуды колебаний в стоячей волне. По измерительной линейке определите длину L₁ резонатора (рас-стояние от телефона до микрофона). Продолжая перемещать поршень, най-дите длины L₂ и L₃ резонатора для двух последующих резонансов. Переме-щая микрофон в обратном направлении, вновь зафиксируйте длины резо-наторов L₃, L₂ и L₁. Указанную процедуру повторите пять раз. Полученные данные запишите в Таблицу 8.2. Запишите в протокол приборную погреш-ность _L определения положений максимумов.

4. 
   Не меняя частоту генератора, установите микрофон в положение L₂. Затем плавным изменением частоты уточните положение резонанса, добиваясь максимального значения амплитуды сигнала на экране осциллографа. За-
   

пишите значение резонансной частоты ₀ и амплитуды колебаний А₀ (в де-лениях сетки экрана осциллографа, условно в миллиметрах) в центральный столбец Таблицы 8.3. Изменяя частоту генератора относительно ₀ в сторо-ну увеличения, а затем уменьшения частоты, запишите соответствующие значения частот _i и амплитуд колебаний А_ в Таблицу 8.3. Максимальное изменение, как в сторону увеличения, так и в сторону уменьшения частоты

выбирайте таким образом, чтобы амплитуда уменьшилась по сравнению с 52

резонансной амплитудой не менее чем в два раза. Шаг изменения частоты выберите в соответствии с градуировкой прибора (частотомера). Запишите

• 
  протокол приборную погрешность определения частоты _ .
  

4. 
   Запишите в Таблицу 8.1 протокола определенную по термометру темпера-
   

туру T, а по барометру – давление p воздуха в лаборатории.
Задание по обработке результатов эксперимента

1. 
   Вычислите для каждого из трех резонансов (n = 1, 2, 3) среднее значение
   

положений Ln каждого резонанса, скорости звука u_n   _n  ₀  2 L n₀ / n и



ее приборных погрешностей _Un .

2. 
   По выборке u_n объема n = 3 и приборным погрешностям _Un вычислите скорость звука u  u  u с P = 95%.
   
3. 
   По экспериментально полученному значению скорости звука u определи-те показатель политропного процесса n и его теплоемкость с. Сопоставьте показатель политропы n с показателем адиабаты для двухатомного газа  1.4 и дайте характеристику процесса распространения звука в воздухе.
   

2. 
   Используя данные Таблицы 8.1 и экспериментально определенное значе-ние показателя политропы n, рассчитайте по формуле скорости звука в га-зах, а также по уравнению Клапейрона p  ( / )RT , плотность воздуха в лаборатории и сопоставьте эти значения друг с другом и с табличным зна-чением плотности воздуха (при нормальных условиях  1.29 кг/м³ ).
   

2. 
   Постройте, используя Таблицу 8.3, экспериментальную резонансную кри-вую (АЧХ резонатора) А_  f ( ) . Определите ее ширину ₀ на уровне
   

A₀ 2.

6. 
   Рассчитайте добротность резонатора по формуле Q = ₀ / ₀.
   

Контрольные вопросы

1. 
   Как направлена колебательная скорость молекул воздуха в акустической волне по отношению к направлению ее распространения?
   

53

2. 
   Какие волны называются стоячими? Как образуются стоячие волны?
   

2. 
   Дайте определение длины бегущей и стоячей волны. Как они взаимосвя-заны друг с другом?
   

2. 
   Свободными или вынужденными являются колебания, возникающие в ре-зонаторе при условиях, заданных в работе? В чем заключается явление ре-зонанса? При каких условиях (длинах резонатора), оно наблюдается?
   

2. 
   Сформулируйте методику измерений, используемую в лабораторной ра-боте, и опишите лабораторную установку.
   

2. 
   Какие колебания называются затухающими? Назовите физические вели-чины, характеризующие затухание колебаний. Каков их физический смысл?
   

2. 
   Дайте определение добротности колебательной системы. Как она вычис-ляется по резонансной кривой (АЧХ), описываемой функцией Лоренца?
   

2. 
   Изобразите качественно график зависимости скорости звука от темпера-туры.
   

2. 
   Что такое степени свободы молекул газа? Как вычисляются полные сте-
   

пени свободы молекул газа с учетом поступательных, вращательных и колебательных степеней свободы молекулы? Рассчитайте полное число степеней свободы для молекул O₂ и CO₂ с учетом и без учета их колеба-тельных степеней свободы.
10. Какие процессы называют политропными? Как вычисляется теплоемкость политропного процесса?

11. 
    Какой процесс называют адиабатным? Что такое показатель адиабаты и чему он равен для двухатомного газа?
    

11. 
    Как связаны между собой мольные и удельные теплоемкости идеального газа в изобарном и изохорном процессах (формула Майера)? Каковы их размерности?
    

54

Работа № 9. ИССЛЕДОВАНИЕ ТЕРМОДИНАМИЧЕСКИХ ЦИКЛОВ
Цель работы:исследование политропно-изохорно-изотермического
(nVT) и адиабатно-изохорно-изотермического (SVT) циклов.
Приборы и принадлежности:баллон с воздухом,манометр,микроком-
прессор, лабораторные термометр и барометр.
			Исследуемые закономерности
Метод измерений. Используемая в работе установка изображена на
рис. 9.1. Баллон А объёмом V1 может сообщаться либо с насосом H, либо с
атмосферой. Внутрь баллона помещён манометр М, измеряющий избыточное
давление. Одно деление шкалы равно 4 мм
вод. ст., что составляет 40 Па. Рабочим газом							А
является воздух. В исходном состоянии пара-							M		H
метры состояния воздуха следующие: внешнее								K
давление p2 и комнатная температура T1. Диа-
грамма	исследуемого		цикла в		координатах			Рис. 9.1.
(p,V) показана на рис. 9.2.
Вначале		насосом	в	баллон	накачивают	р	1
воздух до давления p1			=	p2+p1(рис.9.2		р1		3
(p1; V1)).	При	сжатии	воздух		нагревается,
						р3
поэтому	после закрытия			крана	необходимо	р3			3
выждать некоторое время, пока температура
воздуха в баллоне не сравняется с						р2		2	2
температурой окружающей среды (при этом							V1	V2	V2 V
прекращается движение стрелки манометра).								Рис. 9.2.
Затем воздух выпускают через кран К в атмосферу в течение нескольких
секунд. Когда стрелка манометра приблизится к нулю, кран закрывают. В
этот момент давление воздуха баллоне становится p2 (рис. 9.2 (p2; V2).) Изме-
нение параметров состояния воздуха в процессе расширения отражает линия
12 на рис.9.2,которая является политропой.
					55

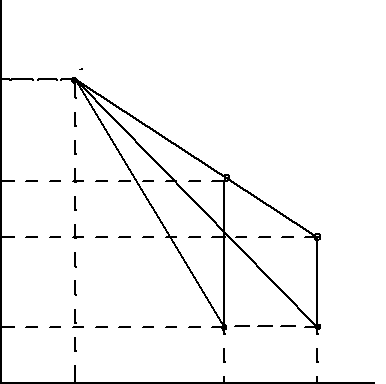После закрытия крана охлаждённый при расширении воздух изохориче-ски нагревается до температуры окружающей среды в результате теплообме-на с ней. Изменение параметров состояния воздуха отражает линия 23 рис. 9.2, которая является изохорой. Температура воздуха в баллоне становится равной температуре в точке 1 (T₃ = T₁), следовательно, точки 1 и 3 лежат на одной изотерме.
После выравнивания температур давление в баллоне изменится на p₃ и станет p₃ = p₂ + p₃ (рис. 9.2 (p₃; V₂)). Таким образом, p₁ и p₃  это изменения давления на участках 12 и 23. Участки 12 и 13 на диаграмме можно аппроксимировать прямыми, так как изменения параметров p, V, T в данной работе малы и много меньше абсолютных значений соответствующих величин.
В работе изучается политропно-изохорно-изотермический (nVT) цикл. Для сравнения с nVT циклом используется адиабатно-изохорно-изотермический (SVT) цикл, отличающийся тем, что процесс расширения га-за на участке 12* рассматривается как адиабатический. Изучение циклов осуществляется путем их моделирования при значениях показателя адиабаты γ=1,4 и показателя политропы n, определенным опытным путем.