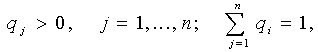Стратегическое мышление и его влияние на принятие стратегических решений. Стратегическое мышление и его влияние на принятие стратегических. Методы разработки и принятия стратегических решений Стратегическое мышление и его влияние на принятие стратегических решений
 Скачать 194.73 Kb. Скачать 194.73 Kb.
|
|
ГЛАВА 3. РАЗРАБОТКА И ПРИНЯТИЕ СТРАТЕГИЧЕСКОГО РЕШЕНИЯ НА ПРИМЕРЕ 3.1. Постановка проблемы В качестве примера разработки и принятия стратегического решения рассмотрим субъекта малого предпринимательства, деятельность которого заключается в розничной реализации цветочной продукции. Предприниматель поставил цель открытия нового павильона «Цветы» и вложить свободные финансовые ресурсы в дело. Как правило, цветочная продукция имеет маленький срок жизни и для успешного развития реализации этого специфичного вида продукции очень важно правильно выбрать место организации торговли, а также выбрать правильную стратегию по реализации. Для начала необходимо выделить основные этапы развития деятельности: 1. Выбор места. 2. Выбор поставщика. 3. Стратегия реализации товара. Каждый этап имеет несколько вариантов решения (альтернативы). Каждая альтернатива имеет свои плюсы и минусы. Также очевидно ,что этапы развития находятся во взаимосвязи между собой. Т. е. выбор поставщика и стратегия реализации напрямую зависят от того, какое решение будет принято на первом этапе. Итак реализацию по решению этой проблемной ситуации можно осуществить следующей последовательностью: * формирование набора параметров по каждому этапу. * оценка их важности * оценка вариантов решения * нахождение оптимального (эффективного) набора решений Таким образом, математическую модель можно представить в следующем виде: F : А ; S (A); P(A) → E(A) где А – множество всех решений по проекту. S - множество связей между решениями . P – сила связей (может быть задана вероятностью, весом и т.д.) E – критерий оптимальности. 3.2. Описание используемых методов и их критериев Во многих задачах финансово-экономической сферы принятие решения осложняется наличием неопределенности, заключающейся в неполноте информации об окружающей эти задачи среде ([1], [2], [5]-[7]). Неопределенность такого типа порождается различными объективными причинами, как то: экономическая и финансовая политика государства, реформы в системе налогообложения, курс валюты, инфляция и т.п. Поэтому в задачах подобного рода принятие решения зависит от объективной действительности, называемой в соответствующей математической модели «природой». Сама же математическая модель называется «игрой с природой», а совокупность принципов и методов построения критериев для принятия оптимальных решений составляет раздел математики «Теория игр с природой», или, другими словами, «Теория статистических решений» ([6], [7]). Таким образом, в игре с природой участвуют два игрока: один из них, обозначим его через А, - лицо, принимающее решение; другой, обозначим его через П, - природа. Игрок Адействует осознанно, стремясь принять наиболее выгодное для себя решение, а природа П, в отличие от него , принимает то или иное свое состояние неопределенным образом, не противодействуя злонамеренно игроку А, не преследуя конкретной цели и абсолютно безразлично к результату игры, т.е. природа П, являясь игроком в игре, не является ни противником, ни союзником игрока А. Пусть игрок А обладает m возможными стратегиями А1,…,Аm, а природа П может находиться в одном из n своих состояний П1,…,Пn. Предполагается обычно, что игрок А в состоянии оценить результаты выбора им каждой из своих стратегий Аi, i=1,…,m, при каждом состоянии природы Пj, j=1,…,n, количественно выражающиеся действительными числами аij. Эти числа, называемые выигрышами игрока А, можно записать в виде матрицы размера m x n, строки которой соответствуют стратегиям игрока А, столбцы – состояниям природы П.
Задача игрока А состоит в выборе оптимальной стратегии, обеспечивающей ему максимально возможный выигрыш. Поскольку стратегии Аi, i=1,…,m, выбираются игроком А осознанно, а не случайно, то их называют чистыми стратегиями, в отличие от смешанных стратегий, которые в данной работе не рассматриваются. Если в распоряжении игрока А всего одна стратегия А1, т.е. m=1, то проблема выбора им оптимальной стратегии отпадает. Поэтому в дальнейшем целесообразно считать m2. Если природа П может пребывать только в одном состоянии П1, т.е. n=1, то проблема выбора игроком А оптимальной стратегии превращается в тривиальную: игрок А должен выбрать стратегию Аk такую, что выигрыши аk1ai1, i=1,…,m. Поэтому целесообразно предполагать, что n2. Если какая-нибудь k-я строка матрицы А доминируется (в частности, дублируется) другой s-й строкой, т.е. (аk1,…,akn)(as1,…asn) (в частности, (аk1,…,akn)=(as1,…asn)), то доминируемую (в частности, дублируемую) k-ю строку можно удалить, как строку, определяющую стратегию Аk, заведомо не лучшую стратегии Аs. В результате матрица А упрощается за счет уменьшения числа строк. Таким образом, в дальнейшем целесообразно считать, что матрица А не содержит доминируемых (в частности, дублируемых строк). Если известны вероятности состояний природы q1=p(П1),…,qn=p(Пn), которые, очевидно, должны удовлетворять условиям:
(поскольку события, состоящие в том, что природа П находится в одном из своих состояний П1,…,Пn, несовместны и составляют полную группу), то говорят о принятии решения «в условиях риска». Если же вероятности, с которыми природа П может находиться в том или ином из своих состояний, неизвестны и отсутствует возможность получения о них какой либо статистической информации, то говорят о принятии решения «в условиях неопределенности». Понятие оптимальности стратегии может определяться различными соображениями, составляющими содержание соответствующих критериев оптимальности. В [3] были проведены некоторые общие соображения относительно конструирования критериев оптимальности различных классов в играх с природой, базирующиеся на введенной в рассмотрение функции игры, которая зависела от выигрышей, рисков и вероятностей состояний природы. В настоящей работе целесообразно применить модифицированный подход к описанию общей методики формирования критериев относительно выигрышей, применимой к выбору оптимальных стратегий как в условиях риска, так и в условиях неопределенности. Целесообразно использовать некоторые известные критерии: Байеса ([1], [2], [5], [7]), Лапласа ([1], [2], [5], [7]), Вальда ([1] – [7]), Ходжа-Лемана ([7]), Гермейера ([7]), критерий произведений ([7]), максимаксный критерий ([1] – [7]), критерий Гурвица ([1] – [7]) и обобщенный критерий Гурвица ([4], [5]). 3.3. Расчет и обоснование вариантов принятия стратегического решения Этап 1. Выбор места для магазина Предприниматель принимает решение о строительстве магазина «цветы» определенного типа в некотором месте. Инвестор действует в условиях неопределенности (информационной непрозрачности) на рынке. Чтобы сформировать представление о ситуации на рынке на момент завершения строительства ему необходимо учесть цены на строительство, конкуренцию на рынке, соотношение предложения и спроса, курсы валют и многое другое. Имеется три варианта (альтернативы) места под магазин: На рынке «Весна», общая площадь магазина 16 м2; (А1) На расстоянии 30 м от рынка «Весна», общая площадь магазина 25 м2; (А2) На противоположной стороне от рынка «Весна», общая площадь магазина 50 м2; (А3) Все три альтернативы имеют свои плюсы и минусы. Как правило рынок имеет большое скопление людей, поэтому близость к рынку «Весна» является большим плюсом и позволяет ускорить процесс освоения нового рынка сбыта, а также позволяет снизить затраты на рекламу. Однако площадь магазина является также немаловажным критерием при решении данной задачи. Большая площадь позволяет расширить ассортимент товара и предлагаемых услуг, а также возможна продажа сопутствующих товаров (например игрушки, подарки, открытки и т.д.). при более детальном изучении этой проблемы могут выявиться и другие немаловажные факторы. Таким образом, перед предпринимателем стоит проблема какому варианту отдать предпочтение. Рассмотрим математическую модель данной ситуации. Мы имеем игру с природой, где игрок А – предприниматель, природа П – совокупность возможных ситуаций на рынке на момент завершения строительства, из которых можно сформировать, например, пять состояний П1, П2, П3, П4, П5 природы. Состояния характеризуются следующим образом: П1 – высокий спрос на продукцию П2 – хороший спрос на продукцию П3 – удовлетворительный спрос на продукцию П3 – низкий спрос на продукцию П4 – низкий спрос на продукцию Необходимо предположить, что предпринимателю известны приближенные вероятности этих состояний q1=p(П1)0,30; q2=p(П2)0,20; q3=p(П3)0,15; q4=p(П4)0,10; q5=p(П5)0,25. Далее необходимо предположить, что предприниматель располагает четырьмя (чистыми) стратегиями А1, А2, А3,представляющими собой выбор определенного места для постройки магазина. Множество этих мест (они были описаны в начале параграфа) ограничено градостроительными решениями, стоимостью земли и т.д. Инвестиционная привлекательность проекта определяется как процент дохода по отношению к сумме капитальных вложений, оценка которых известна (предполагается ее известность из личного опыта предпринимателя, интуиции, проведенного маркетингового исследования при каждой стратегии и каждом состоянии природы). Предприниматель рассуждает следующим образом: Стратегия А1. "Если я арендую магазин на рынке за 1000 руб в день, то при П3 я смогу продать в среднем 200 цветов по цене 50 руб. за штуку (предварительно я покупаю оптом по цене 30 руб за шт.) и моя выручка составит 10 тыс. руб., затраты 7 тыс. руб., а прибыль 3 тыс. руб., но т.к. магазин маленький я не могу продавать больше и расширить ассортимент продукции и продавать сопутствующие товары". Аналогично он рассуждает и для остальных состояний П. см. табл. 3.1. Стратегия А2. "Если я арендую магазин рядом с рынком за 1500 руб в день, то при П3 я смогу продать в среднем 180 цветов (меньше цветов, чем при А1, т.к. меньше посетителей у моего магазина) по цене 50 руб. за штуку (предварительно я покупаю оптом по цене 30 руб за шт.), но зато я могу продавать сопутствующие товары и расширять ассортимент продукции" Аналогично он рассуждает и для остальных состояний П. см. табл. 3.1. Стратегия А3. "Если я арендую магазин напротив рынка за 1800 руб в день, то при П3 я смогу продать в среднем 150 цветов (меньше цветов, чем при А1, т.к. меньше посетителей у моего магазина) по цене 50 руб. за штуку (предварительно я покупаю оптом по цене 30 руб за шт.), но зато я могу продавать значительно больше сопутствующих товаров товары и расширять наасортиемнт продукции". Вналогично он рассуждает и для остальных состояний П. см. табл. 4. Таблица 4. Рассуждения предпринимателя в зависимости от состояний природы и варианта альтернативы
Эти данные представлены в следующей матрице выигрышей (прибылей) предпринимателя:
размера 3 х 5, в последней, дополнительной строке которой указаны вероятности состояний природы. Матрица (24) не содержит доминируемых (в частности, дублируемых) строк и все ее элементы положительны. Предпринимателю предстоит выбрать участок земли так, чтобы наиболее эффективно использовать капиталовложения. Целесообразно подсчитать показатели эффективности стратегий по критериям Байеса, Гермейера и критерию произведений при условии, что предприниматель доверяет данному распределению вероятностей состояний природы, по критерию Лапласа, если предприниматель не доверяет данному распределению вероятностей состояний природы и не может отдать предпочтения ни одному из рассматриваемых состояний природы, по критерию Ходжа-Лемана с коэффициентом доверия к вероятностям состояний природы, например, l=0,4, по критерию Вальда, максимаксному критерию, критерию пессимизма-оптимизма Гурвица с показателем оптимизма, например, l=0,6, и по обобщенному критерию Гурвица с коэффициентами, например, l1=0,35; l2=0,24; l3=0,19; l4=0,13; l5=0,09. Результаты подсчета показателей эффективности и оптимальные стратегии представлены в следующей таблице (см. табл. 5): Таблица 5. Таблица показателей эффективности и оптимальных стратегий
Необходимо отметить, что, поскольку, в критерии Ходжа-Лемана показатель доверия предпринимателя распределению вероятностей состояний, указанных в последней строке матрицы (24), равен l=0,4, то показатель пессимизма предпринимателя равен 1-l=0,6. В критерии Гурвица показатель оптимизма игрока А равен l=0,4 и, следовательно, показатель его пессимизма также равен 1-l=0,6. В обобщенном критерии Гурвица по формуле (23) показатель пессимизма 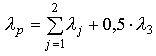 = 0,35+0,24+0,5×0,19=0,685 = 0,35+0,24+0,5×0,19=0,685и, следовательно, показатель оптимизма l0=1-0,685=0,315. Таким образом, во всех примененных критериях, учитывающих индивидуальные проявления к пессимизму и оптимизму, предприниматель более склонен к пессимистической оценке ситуации, чем к оптимистической, примерно с одинаковыми показателями. В результате применения девяти критериев можно сказать, что в качестве оптимальной стратегии А1 выступает 5 раз, стратегия А3 – 4 раза и стратегия А2 – 0 раз. Поэтому, если у инвестора А нет никаких обоснованных серьезных возражений, то в качестве оптимальной можно рассматривать стратегию А1. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||