|
|
задания по МОДО. ИтоговаяРабота - 4 группа. Методические рекомендации по использованию задач на уроке. Методические материалы для учителей математики общеобразовательных школ
Методы решения задач по статистике и теории вероятностей в основной школе
1.задание
Тема:
|
Элементы комбинаторики и их применение для нахождения вероятности событий.
|
Цель обучения:
|
10.3.2.4 - понимать и применять правила умножения вероятностей
* P(A ∙ B) = P(A) ∙ P(B)
|
Условие задачи:
|
В классе 12 мальчиков и 10 девочек. Чтобы посадить цветы нужно 2 мальчика и 2 девочки. Сколькими способами это можно сделать?
|
Решение:
|
Из 12 мальчиков выбрать двоих, сделаем это по формуле «сочетания» С122 = 66
Аналогично найдём сколькими способами выберем две девочки из 10
С102 =45
В условии говарится что нам надо И два мальчика И две девочки- это правило УМНОЖЕНИЯ
С122 ∙ С102 =66*45 =2970
|
Ответ:
|
2970
|
Методические рекомендации по использованию на уроке:
|
Можно предложить лля самостоятельного разбора задачи, но если возникнут вопросы разобрать совместно
|
2. задание
Тема:
|
Основы теории вероятностей
Элементы комбинаторики и их применение для нахождения вероятности событий.
|
Цель обучения:
|
10.3.1.1 - различать понятия: «перестановки», «размещения» и «сочетания» без повторений и с повторениями;
10.3.1.2 - применять формулы для вычисления перестановок, сочетаний, размещений без повторений;
10.3.1.3 - применять формулы для вычисления перестановок, сочетаний, размещений с повторениями;
|
Условие задачи:
|
Сколькими способами могут разместиться 7 человек в очереди за билетами в театр?
|
Решение:
|
Воспользуемся формулой «размещения» Р!
7!=1·2·3·4·5·6·7=5040
|
Ответ:
|
5040
|
Методические рекомендации по использованию на уроке:
|
Можно предложить для самостоятельного решения учащимся
|
3.задание
Тема:
|
Основы теории вероятностей
|
Цель обучения:
|
9.3.2.3 знать классическое определение вероятности и применять его для решения задач
|
Условие задачи:
|
На тарелке 20 пирожков: 2 с мясом, 16 с капустой и 2 с вишней. Рома наугад выбирает один пирожок. Найдите вероятность того, что он окажется с вишней
|
Решение:
|
С вишней всего 2 пирожка
Находим вероятность наугад выбранного пирожка с вишней их общего количества 20.
2/20 = 1/10 = 0,1
|
Ответ:
|
0,1
|
Методические рекомендации по использованию на уроке:
|
Можно использовать для закрепления понятия вероятности при разборе темы, а так же в тестах на проверку знаний
|
4.задание
Тема:
|
Вариационные ряды
|
Цель обучения:
|
7.3.3.1 усвоить понятия генеральной совокупности, случайной выборки, вариационного ряда, варианты;
|
Условие задачи:
|
Десять учеников проверили свои знания по математике на пробном тестировании и получили следующие баллы:
15, 10,18, 25, 12, 18, 15, 10, 18, 12.
а) Составьте вариационный ряд;
б) Напишите распределение частот выборки;
|
Решение:
|
а)10, 10, 12, 12, 15, 15, 18, 18, 18, 25.-вариационный ряд
б)
|
Ответ:
|
|
Методические рекомендации по использованию на уроке:
|
Можно использовать в заданиях формативного оценивания на закрепление. При работе в группах при изучении нового материала, на повторении при подготовки к СОР или СОЧ.
|
5.задание
Тема:
|
Статистические данные и их характеристики: среднее арифметическое, мода, медиана, размах
|
Цель обучения:
|
6.4.3.1 знать определения среднего арифметического нескольких чисел, размаха, медианы и моды ряда числовых данных;
6.4.3.2 вычислять статистические числовые характеристики;
|
Условие задачи:
|
Среди учащихся 5 классов был проведен опрос: сколько времени вы тратите на выполнение домашнего задания по математике. Были получены следующие результаты (в минутах): 11, 12, 15, 20, 15, 14, 18.
Для данного ряда данных найдите:
а) моду,
б) среднее значение,
в) размах,
г) медиану
|
Решение:
|
а) мода-15
б) (11+12+15+20+15+14+18)=105:7=15-среднее арифметическое
в)20-11=9-размах
г) 11,12,14,15,15,18,20
15-медиана числового ряда
|
Ответ:
|
а)15, б)15, в)9 г) 15
|
Методические рекомендации по использованию на уроке:
|
Можно использовать при формативном оценивании.
При закреплении в тестах при повторении и закреплении пройденного материала.
|
6.задание
Тема:
|
Основы теории вероятностей
|
Цель обучения:
|
9.3.2.3 знать классическое определение вероятности и применять его для решения задач;
9.3.2.4 знать статистическое определение вероятности;
|
Условие задачи:
|
Для проверки качества изделий было исследовано 200 деталей, среди которых 5 оказались бракованными.
а) Найдите вероятность того, что наугад взятая деталь будет пригодной.
b) Сколько в среднем бракованных деталей окажется в партии из 1000 деталей?
|
Решение:
|
а)200-5=195(дет) пригодные
Р(А)= 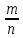 = =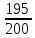 =0.975 =0.975
б)Р(А)= 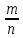 = =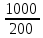 =5 =5
5 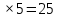 (дет)-бракованных (дет)-бракованных
|
Ответ:
|
а)0,975
б)25 деталей
|
Методические рекомендации по использованию на уроке:
|
Можно использовать при объяснении и закреплении нового материала, в заданиях СОР или СОЧ.
|
7.задание
Тема:
|
Абсолютная частота и относительная частота. Таблица частот
|
Цель обучения:
|
7.3.3.2 вычислять абсолютную и относительную частоты варианты;
|
Условие задачи:
|
Для итоговой контрольной работы был создан тест из 8 заданий. Количество верных ответов, полученных каждым из 50 учащихся, было представлено в виде таблицы частот. Найдите пропущенное значение частоты.
Число верных ответов
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
Частота
|
2
|
4
|
2
|
6
|
|
11
|
7
|
7
|
2
|
|
Решение:
|
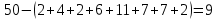
|
Ответ:
|
9
|
Методические рекомендации по использованию на уроке:
|
Возможно использование на фо, сор, для закрепления материала
|
8.задание
Тема:
|
Среднее значение. Дисперсия. Стандартное отклонение
|
Цель обучения:
|
8.3.3.3 знать определение накопленной частоты;
|
Условие задачи:
|
Заполните таблицу:
Расстояние (км)
|
Частота
|
Накопленная частота
|
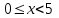
|
|
19
|
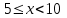
|
26
|
|
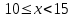
|
|
75
|
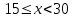
|
|
148
|
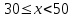
|
32
|
|
|
Решение:
|
Расстояние (км)
|
Частота
|
Накопленная частота
|
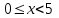
|
19
|
19
|
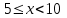
|
26
|
45
|
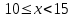
|
30
|
75
|
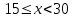
|
73
|
148
|
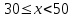
|
32
|
180
|
|
Ответ:
|
Ответ представлен в таблице
|
Методические рекомендации по использованию на уроке:
|
Возможно использование на фо, сор, для закрепления материала
|
9.задание
Тема:
|
Вариационные ряды
|
Цель обучения:
|
7.3.3.1 усвоить понятия генеральной совокупности, случайной выборки, вариационного ряда, варианты;
|
Условие задачи:
|
Измерьте длину фосолин, запишите выборку в вариационный ряд.
|
Решение:
|
Учащиеся измеряют самостоятельно длину нескольких фасолин, записывают все в вариационный ряд. Таким образом, осваивают понятия случайной выборки и вариационного ряда.
|
Ответ:
|
Ответ будет представлен в виде вариациооного ряда.
|
Методические рекомендации по использованию на уроке:
|
Возможно использование на фо, для закрепления материала, если принести фасоль в класс, либо на дз, если учащиеся имеют возможность купить фасоль сами.
|
10.задание
Тема:
|
Бином Ньютона и его свойства
|
Цель обучения:
|
9.3.1.6 знать и применять формулу бинома Ньютона и его свойства
|
Условие задачи:
|
В биноминальном разложении ( 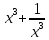 )18 найти член разложения не содержащий х )18 найти член разложения не содержащий х
|
Решение:
|
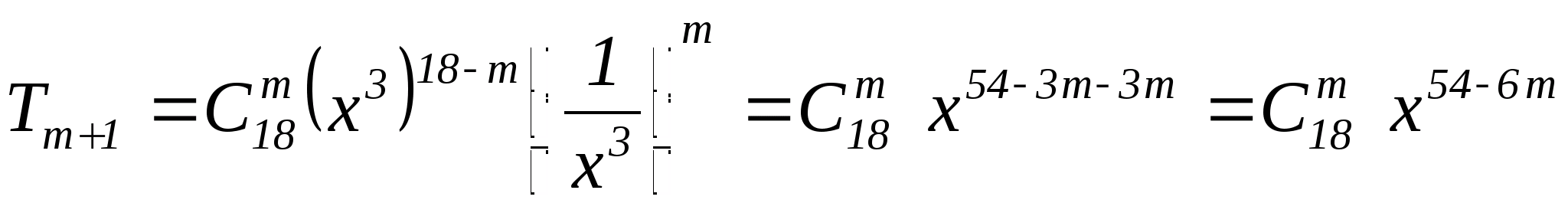
Так как в разложении мы ищем член не содержащий х, то 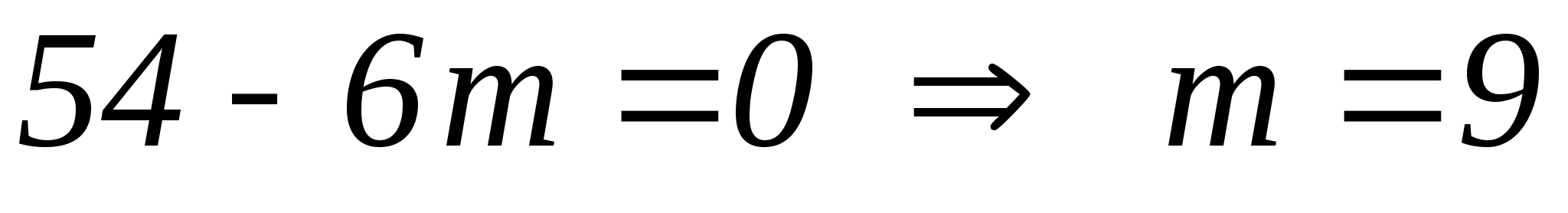
Тогда
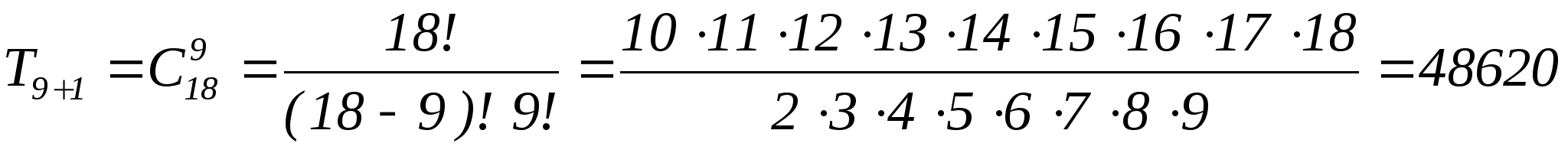
|
Ответ:
|
Ответ: 48620.
|
Методические рекомендации по использованию на уроке:
|
Урок закрепления ззнаний
|
11.задание
Тема:
|
Основы теории вероятностей
|
Цель обучения:
|
9.3.2.3 знать классическое определение вероятности и применять его для решения задач
|
Условие задачи:
|
Набирая номер телефона, абонент забыл две последние цифры, но помнит, что эти цифры различны и первая цифра больше второй. Найти вероятность того, что набран правильный номер
|
Решение:
|
Найдем общее число исходов
Возможная предпоследняя цифра номера
|
Возможные последние цифры:
|
Количество исходов:
|
1
|
0
|
1
|
2
|
0;1
|
2
|
3
|
0;1;2
|
3
|
4
|
0;1;2;3
|
4
|
5
|
0;1;2;3;4
|
5
|
6
|
0;1;2;3;4;5
|
6
|
7
|
0;1;2;3;4;5;6
|
7
|
8
|
0;1;2;3;4;5;6;7
|
8
|
9
|
0;1;2;3;4;5;6;7;8
|
9
|
Всего: 45 возможных исходов. Благоприятствующий исход – один. По классическому определению: Р=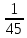 – вероятность того, что абонент наберет правильный номер Р= – вероятность того, что абонент наберет правильный номер Р= 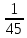  0,022 0,022
|
Ответ:
|
Р= 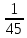  0,022 0,022
|
Методические рекомендации по использованию на уроке:
|
При изучении материала
|
12.задание
Тема:
|
Элементы статистики
|
Цель обучения:
|
7.3.3.2вычислять абсолютную и относительную частоты варианты;
|
Условие задачи:
|
В тестировании принимали участие 75 учащихся. Для проведения статистического исследования был записан результат каждого пятого учащегося: 23, 24, 16, 21, 18, 17, 20, 23, 18, 16, 19, 18, 22, 19, 21. Заполните таблицу абсолютных и относительных частот.
|
Решение:
|
Решение:
Результаты теста
|
16
|
17
|
18
|
19
|
20
|
21
|
22
|
23
|
24
|
Абсолютная частота
|
2
|
1
|
3
|
2
|
1
|
2
|
1
|
2
|
1
|
Относительная частота
|
|
|
|
|
|
|
|
|
|
|
Ответ:
|
|
Методические рекомендации по использованию на уроке:
|
При изучении материала
|
|
|
|
 Скачать 1.7 Mb.
Скачать 1.7 Mb.
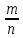 =
=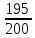 =0.975
=0.975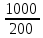 =5
=5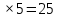 (дет)-бракованных
(дет)-бракованных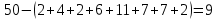
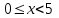
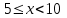
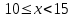
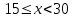
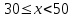
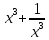 )18 найти член разложения не содержащий х
)18 найти член разложения не содержащий х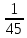 – вероятность того, что абонент наберет правильный номер Р=
– вероятность того, что абонент наберет правильный номер Р=  0,022
0,022