Статистика и теория вероятностей в старших классах
1.задание
Тема:
|
Теория вероятности
|
Цель обучения:
|
10.3.1.4 - решать задачи на нахождение вероятностей, применяя формулы комбинаторики;
|
Условие задачи:
|
Сколькими способами можно рассадить 6 человек за столом, на котором стоят 6 различных приборов?
|
Решение:
|
Число способов рассаживания гостей равно числу перестановок из 6 элементов.
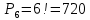
|
Ответ:
|
720 способов
|
Методические рекомендации по использованию на уроке:
|
Задачу можно использовать при закреплении материала, для самостоятельного решения при дифференциации.
|
2.задание
Тема:
|
Теория вероятности
|
Цель обучения:
|
10.3.1.4 - решать задачи на нахождение вероятностей, применяя формулы комбинаторики;
|
Условие задачи:
|
В чемпионате страны по футболу принимают участие 15 команд. Сколько существует способов распределить золотую, серебряную и бронзовую медали? Решение.
|
Решение:
|
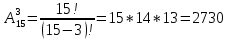
|
Ответ:
|
2730 способов
|
Методические рекомендации по использованию на уроке:
|
Задачу можно использовать при закреплении материала, для самостоятельного решения при дифференциации.
|
3.задание
Тема:
|
Теория вероятности
|
Цель обучения:
|
10.3.1.4 - решать задачи на нахождение вероятностей, применяя формулы комбинаторики;
|
Условие задачи:
|
У студента есть 5 книг, из которых надо прочитать
ровно 2. Сколькими способами можно выбрать эти книги?
|
Решение:
|
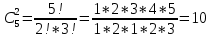
|
Ответ:
|
10 способов
|
Методические рекомендации по использованию на уроке:
|
Задачу можно использовать при закреплении материала, для самостоятельного решения при дифференциации.
|
4.задание
Тема:
|
Среднее значение. Дисперсия. Стандартное отклонение.
|
Цель обучения:
|
8. 3.3.5 - знать определения и формулы для вычисления дисперсии и стандартного отклонения.
|
Условие задачи:
|
Закон распределения дискретной случайной величины Х заданы таблицей:
Вычислить дисперсию D(X) и стандартное отклонение
Ϭ(X).
|
Решение:
|
Согласно свойствами дисперсии получим:
D(X)=M(X2)-M2(X)=
M(X)= -2*0,2-1*0,1+1*0,3+5*0,2+6*0,1=1,7
M(X2)=(-2)2 *0,2+(-1)2*0,1+1*0,3+52*0,2+62*0,1=10,7
D(X)=10,7-1,72=10,7-2,89=7,81
Ϭ(X)=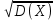 = =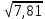 =2,79 =2,79
|
Ответ:
|
7,81; 2,79
|
Методические рекомендации по использованию на уроке:
|
Можно использовать для закрепления формул при индивидуальной работе.
|
5.задание
Тема:
|
Условная вероятность. Правила сложения и умножения вероятностей
|
Цель обучения:
|
10.3.2.4 - понимать и применять правила умножения вероятностей
* P(A ∙ B) = P(A) ∙ P(B)
* P(A ∙ B) = P(A) ∙ PA(B) = P(B) ∙ PB(A);
|
Условие задачи:
|
Из урны, в которой находятся 12 белых и 8 черных шаров, вынимают наудачу два шара. Какова вероятность того, что оба шара окажутся черными?
|
Решение:
|
Событие A- появление двух черных шаров. Общее число возможных случаев n равно числу сочетаний из 20 элементов (12+8) по 2
n== = 190
Число случаев m, благоприятствующих событию A, составляет
n== = 28
P(A)= = = = 0,147
|
Ответ:
|
0,147
|
Методические рекомендации по использованию на уроке:
|
Для самостоятельного решения
|
6.задание
Тема:
|
Условная вероятность. Правила сложения и умножения вероятностей
|
Цель обучения:
|
10.3.2.4 - понимать и применять правила умножения вероятностей
* P(A ∙ B) = P(A) ∙ P(B)
* P(A ∙ B) = P(A) ∙ PA(B) = P(B) ∙ PB(A);
|
Условие задачи:
|
В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах
|
Решение:
|
Определим события
А = {кофе закончится в первом автомате},
В = {кофе закончится во втором автомате},
А ∙ В = {кофе закончится в обоих автоматах},
А + В = {кофе закончится хотя бы в одном автомате}.
По условию задачи P(A)=P(B)=0,3 и P(A × B)=0,12
События A и B совместные, вероятность суммы двух совместных событий равна сумме вероятностей этих событий, уменьшенной на вероятность их произведения:
P(A + B) = P(A) + P(B) − P(A·B) = 0,3 + 0,3 − 0,12 = 0,48.
Следовательно, вероятность противоположного события, состоящего в том, что кофе останется в обоих автоматах, равна 1 − 0,48 = 0,52.
|
Ответ:
|
0,52
|
Методические рекомендации по использованию на уроке:
|
Для работы в группе
|
7.задание
Тема:
|
Условная вероятность. Правила сложения и умножения вероятностей
|
Цель обучения:
|
10.3.2.4 - понимать и применять правила умножения вероятностей
* P(A ∙ B) = P(A) ∙ P(B)
* P(A ∙ B) = P(A) ∙ PA(B) = P(B) ∙ PB(A);
|
Условие задачи:
|
По отзывам покупателей Иван Иванович оценил
надёжность двух интернет-магазинов. Вероятность того, что нужный товар доставят из магазина А, равна 0,8. Вероятность того, что этот товар доставят из магазина Б, равна 0,9. Иван Иванович заказал товар сразу в обоих магазинах. Считая, что интернет-магазины работают независимо друг от друга, найдите вероятность того, что ни один магазин не доставит товар
|
Решение:
|
Вероятность того, что первый магазин не доставит товар равна 1 − 0,8 = 0,2.
Вероятность того, что второй магазин не доставит товар равна 1 − 0,9 = 0,1.
Поскольку эти события независимы, вероятность их произведения (оба магазина не доставят товар) равна произведению вероятностей этих событий: 0,2 · 0,1 = 0,02
|
Ответ:
|
0,02
|
Методические рекомендации по использованию на уроке:
|
Для самостоятельного решения
|
8.задание
Тема:
|
Определение классической вероятности. Статистическая вероятность
|
Цель обучения:
|
9.3.2.1 усвоить понятия: событие, случайное событие, достоверное событие, невозможное событие, благоприятствующие исходы, равновозможные и противоположные события;
9.3.2.2 различать элементарное событие от неэлементарного;
|
Условие задачи:
|
На каждой из пяти одинаковых карточек напечатана одна из следующих букв: "а", "м", "р", "т", "ю". Карточки тщательно перемешаны. Найти вероятность того, что на четырех вынутых по одной карточке можно прочесть слово "юрта".
|
Решение:
|
Используем классическое определение вероятности:
P= 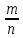 , где m - число исходов, благоприятствующих осуществлению события, а n - число всех равновозможных элементарных исходов. , где m - число исходов, благоприятствующих осуществлению события, а n - число всех равновозможных элементарных исходов.
n=5⋅4⋅3⋅2=120 способов, так как первую карточку (букву) можно вытянуть (выбрать) 5 способами (так как всего карточек пять), вторую - 4 (осталось к этому шагу четыре), третью - 3 и четвертую - 2 способами.
m=1 , так как искомая последовательность карточек "ю", потом "р", потом "т", потом "а" только одна.
Получаем вероятность P=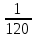
|
Ответ:
|
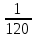
|
Методические рекомендации по использованию на уроке:
|
Задачу можно использовать при повторении понятия вероятности при групповой работе.
|
9.задание
Тема:
|
Сочетания без повторений
|
Цель обучения:
|
10.3.1.2 - применять формулы для вычисления перестановок, сочетаний, размещений без повторений;
|
Условие задачи:
|
В классе 20 учащихся. Сколькими способами можно выделить двух человек для дежурства?
|
Решение:
|
Так как каждая группа учащихся в 2 человека должна отличаться хотя бы одним из учащихся. Отсюда, применим формулу комбинаторики — сочетание, имеем
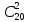 = =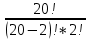 = =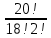 = =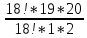 = =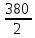 =190 =190
|
Ответ:
|
190
|
Методические рекомендации по использованию на уроке:
|
Задачу можно использовать на закрепление формулы сочетания без повторений при формативном оценивании.
|
10.задание
Тема:
|
Формула полной вероятности и формула Байеса
|
Цель обучения:
|
10.3.2.6 - знать формулу Байеса и применять ее при решении задач;
|
Условие задачи:
|
На вход радиолокационного устройства с вероятностью 0,8 поступает смесь полезного сигнала с помехой, а с вероятностью 0,2 – только помеха. Если поступает полезный сигнал с помехой, то прибор регистрирует наличие какого-то сигнала с вероятностью 0,7; если только помеха – то с вероятностью 0,3. Известно, что устройство зарегистрировало наличие какого-то сигнала. Найти вероятность того, что в его составе есть полезный сигнал.
|
Решение:
|
По условию:
р1 = 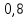 - вероятность того, что поступит смесь полезного сигнала с помехой., - вероятность того, что поступит смесь полезного сигнала с помехой.,
р2 = 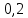 - вероятность того, что поступит только помеха. - вероятность того, что поступит только помеха.
Р3 =0,7 – вероятность того, что прибор зарегистрирует какой-то сигнал, когда поступила смесь полезного сигнала с помехой,
р4 =0,3 - вероятность того, что прибор зарегистрирует какой-то сигнал, когда поступила только помеха.
По формуле полной вероятности:
р = р1 р3 + р2 р4 = 0,8*0,7 + 0,2*0,3 = 0,56 + 0,06 = 0,62 - вероятность того, что прибор зарегистрирует какой-то сигнал.
По формуле Байеса:
Р=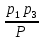 = = 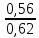 = = 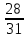 – вероятность того, что в зарегистрированном сигнале содержится полезный сигнал – вероятность того, что в зарегистрированном сигнале содержится полезный сигнал
|
Ответ:
|
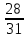  0,9032 0,9032
|
Методические рекомендации по использованию на уроке:
|
При решении задач на закрепление.
|
11.задание
Тема:
|
Элементы комбинаторики и их применение для нахождения вероятности событий.
|
Цель обучения:
|
10.3.1.4 - решать задачи на нахождение вероятностей, применяя формулы комбинаторики;
|
Условие задачи:
|
В ящике находятся не отличающиеся друг от друга 8 деталей, среди которых 5 окрашенных. Наудачу извлекают 5 деталей. Найдите вероятность того, что две из них окажутся не окрашенными. Ответ округлите до десятых.
|
Решение:
|
Пусть событие А состоит в том, что среди пяти извлеченных деталей окажутся 3 окрашенные и 2 не окрашенные.
Для вычисления вероятности события воспользуемся формулой
P(A) = 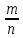
Cреди извлеченных деталей должны оказаться 3 окрашенные из 5 и 2 не окрашенные из 3 (8-5=3). Поэтому m = 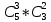 . .
Так как отбирается 5 деталей из 8, то общее число случаев равно:
n =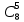
P(A) = 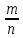 = = 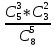 = = 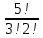 * *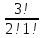 : :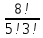 = =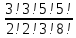 = = 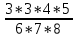 = = 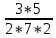 = = 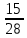  0,5 0,5
|
Ответ:
|
 0,5 0,5
|
Методические рекомендации по использованию на уроке:
|
При изучении материала
|
12.задание
Тема:
|
Формула Бернулли и ее следствия
|
Цель обучения:
|
10.3.2.8 - использовать формулу Бернулли и ее следствия при решении задач;
|
Условие задачи:
|
В каждой из восьми урн имеется 10 белых и 5 черных шаров. Из каждой урны извлекли по одному шару. Что вероятнее: появление двух черных и шести белых или трех черных и пяти белых шаров?
|
Решение:
|
Из условия находим: 10 + 5 = 15 шаров в каждой урне.
По классическому определению: p = 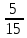 = = 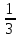 , q = , q = 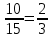 – вероятности извлечения черного и белого шара соответственно из каждой урны. Используем формулу Бернулли: – вероятности извлечения черного и белого шара соответственно из каждой урны. Используем формулу Бернулли: 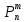 = = 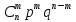
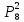 = = 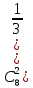 = = 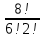 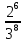 = = 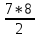 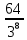 = = = = 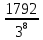 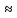 0,2731 – вероятность того, что будут извлечены 2 черных и 6 белых шаров. 0,2731 – вероятность того, что будут извлечены 2 черных и 6 белых шаров.
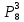 = = 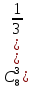 = = 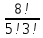 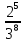 = = 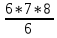 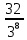 = = = = 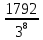  0,2731 – вероятность того, чтобудут извлечены 3 черных и 5 белых шаров. 0,2731 – вероятность того, чтобудут извлечены 3 черных и 5 белых шаров.
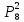 = = 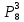 данные события равновероятны данные события равновероятны
|
Ответ:
|
данные события равновероятны
|
Методические рекомендации по использованию на уроке:
|
При изучении материала или ф.о.
| |
 Скачать 1.7 Mb.
Скачать 1.7 Mb.
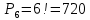
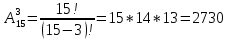
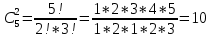
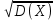 =
=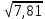 =2,79
=2,79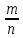
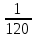
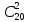 =
=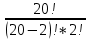 =
=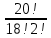 =
=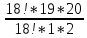 =
=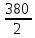 =190
=190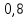 - вероятность того, что поступит смесь полезного сигнала с помехой.,
- вероятность того, что поступит смесь полезного сигнала с помехой., 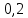 - вероятность того, что поступит только помеха.
- вероятность того, что поступит только помеха.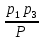 =
= 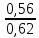 =
= 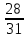 – вероятность того, что в зарегистрированном сигнале содержится полезный сигнал
– вероятность того, что в зарегистрированном сигнале содержится полезный сигнал 0,9032
0,9032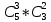 .
.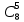
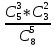 =
= 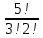 *
*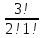 :
: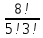 =
=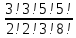 =
= 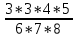 =
= 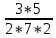 =
= 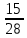
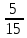 =
= 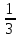 , q =
, q = 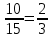 – вероятности извлечения черного и белого шара соответственно из каждой урны. Используем формулу Бернулли:
– вероятности извлечения черного и белого шара соответственно из каждой урны. Используем формулу Бернулли: 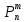 =
= 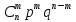
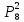 =
= 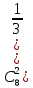 =
= 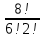
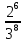 =
= 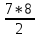
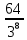 = =
= = 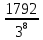
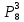 =
= 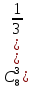 =
= 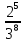 =
= 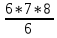
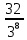 = =
= =